相対論的流体の熱統計力学
ここでは、相対論的なガス(流体)の熱統計力学について見ていきましょう。 相対論的な流体を構成する物質の状態方程式や、熱平衡について理解することを目指します。
熱力学
相対論では、粒子のエネルギーに静止質量エネルギーが含まれることから、ガスの内部エネルギーは静止質量のエネルギーを含んで定義されなければなりません。 一定量の物質を考え、その内部エネルギーを\(U\)、体積を\(V\)、圧力を\(P\)、温度を\(T\)、エントロピーを\(S\)としましょう。 熱力学の第一法則より、準静的な変化に対して
\[dU = -P dV + T dS \tag{1}\]となります。 一般に相対論的な温度では、粒子の対生成や対消滅が起こります。 そのため粒子数は保存しませんが、考えている一定量の物質を特徴付ける粒子数\(N\)が存在すると仮定しましょう (例えば考えている物質に含まれるバリオン数などを考えれば良いでしょう。) 数密度は\(n = N/V\)であり、粒子数保存は
\[dn = -\frac{n}{V} dV \tag{2}\]のようになります。 内部エネルギー密度\(\varepsilon = U / V\)の変化は
\[d\varepsilon = \frac{\varepsilon + P}{n} dn + nTds \tag{3}\]となります。 ここで\(s = S/N\)は、1粒子辺のエントロピーです。
物質の出入りがある場合は、1粒子辺の化学ポテンシャル\(\mu\)を用いて
として、非相対論的な場合の熱力学と同様の考察を進めれば良いでしょう。 非相対論的な場合と同様に
\[\mu N = U - TS + PV \ \Longrightarrow \ \mu = \frac{U}{N} - \frac{TS}{N} + P \frac{V}{N} = \frac{U}{nV} - sT + \frac{P}{n} = \frac{\varepsilon + P - ns T}{n} \tag{5}\]の関係式が成り立ちます。 ここからわかるように、\(\mu\)にも静止質量エネルギーが加わっています。 このように、相対論的な熱力学は、非相対論的な場合と全く同様に定式化することが可能です。 熱力学量は考えている一定量の物質の固有系で意味を持つ物理量であり、熱力学の法則はこの固有系で成立するものです。 したがって、温度などの熱力学量のローレンツ変換に対する変換性を一般的に議論することには、意味がないことに注意しましょう。
高原さんの特殊相対論にはこのように書いてあり、私もまぁ概ね同意です。
しかし今もなお議論を呼ぶ分野でもあるため、これを考えることには何かしら意味があるのかも、とも思います。
熱平衡
熱平衡状態が温度\(T\)で指定されることは、非相対論的な場合と全く同様です。 熱平衡の概念はもちろん考えている物質の固有系でしか意味がありません。 熱平衡状態での位相空間分布関数も、非相対論的な場合と同様に
\[f(\mathbf{p}) = \frac{g}{h^3} \frac{1}{e^{\frac{E-\mu}{k_B T}} \pm 1} \tag{6}\]のように書かれます。 ここで、\(g\)はスピンによる統計的重率、\(h\)はプランク定数、\(k_B\)はボルツマン定数です。 分母のプラス符号はフェルミ粒子、マイナス符号はボーズ粒子の場合に対応します。 ただし、相対論的な熱平衡を考える場合には、\(E, \mu\)が静止質量エネルギーを含んで定義されているということです。 熱平衡にある光子気体の分布関数はよく知られたプランク分布であり、質量がゼロかつ\(g=2, \mu=0\)のボーズ粒子としたものです。 光子はプランク分布に従い、その数密度は
\[n_\gamma = \frac{2\zeta(3)}{\pi^2} \left( \frac{k_B T}{\hbar c}\right)^3 \tag{7}\]そしてエネルギー密度は
\[\varepsilon_\gamma = \frac{\pi^2}{15} \frac{(k_B T)^4}{\hbar^3 c^3} \tag{8}\]のように計算されます。 ここで\(\zeta\)はリーマンのゼータ関数、\(\hbar = h / (2\pi)\)です。
量子力学の効果が無視できる場合、(6)式の分母の\(\pm 1\)の項が無視でき、相対論的なマクスウェル・ボルツマン分布
となります。 これを運動量で積分することで、数密度を計算しましょう。 今、系は等方的であるとして
\[n = \iiint f(\mathbf{p}) d^3 \mathbf{p} = 4\pi \int_0^\infty p^2 f(p) dp = \frac{4\pi g}{h^3} e^{\frac{\mu}{k_B T}} \int_0^\infty p^2 e^{-\frac{E}{k_B T}} dp\]となります。 ここで\(E = \sqrt{m^2 c^4 + c^2 p^2}\)から、\(p dp = \frac{E}{c^2}dE\)より
\[n = \frac{4\pi g}{h^3} e^{\frac{\mu}{k_B T}} \int_{mc^2}^\infty \frac{\sqrt{E^2 - m^2 c^4}}{c} e^{-\frac{E}{k_B T}} \frac{E}{c^2} dE = \frac{4\pi g}{h^3 c^3} e^{\frac{\mu}{k_B T}} \int_{mc^2}^\infty E \sqrt{E^2 - m^2 c^4} e^{-\frac{E}{k_B T}} dE\]のように整理されます。 さらに\(x = \frac{E}{mc^2}, T_\ast = \frac{k_B T}{mc^2}\)のように無次元化した量を導入すると
\[n = \frac{4\pi g}{h^3 c^3} e^{\frac{\mu}{k_B T}} \int_1^\infty m^2 c^4 x \sqrt{x^2 - 1} e^{-x/T_\ast} mc^2 dx = 4\pi g \left( \frac{mc}{h} \right)^3 e^{\frac{\mu}{k_B T}} \int_1^\infty x \sqrt{x^2 - 1} e^{-x/T_\ast} dx\]となります。 ここで第二種修正ベッセル関数の公式
\[\int_1^\infty x (x^2 - 1)^{1/2} e^{-x/T_\ast} dx = T_\ast K_2 (1/T_\ast)\]を用いると
\[n = 4\pi g \left( \frac{mc}{h}\right)^3 e^{\frac{\mu}{k_B T}} T_\ast K_2(1/T_\ast) \tag{10}\]のようになります。 これを用いて(9)式から\(\frac{g}{h^3} e^{\frac{\mu}{k_B T}}\)を消去すれば
\[f(\mathbf{p}) = \frac{n}{4\pi (mc)^3 T_\ast K_2(1/T_\ast)} e^{-\frac{E}{k_B T}} \tag{11}\]を得ます。 さらにこれを用いて、エネルギー密度および圧力が
\[\varepsilon = \pi g e^{\frac{\mu}{k_B T}} \left( \frac{mc}{h} \right)^3 k_B T \{ 3K_3(1/T_\ast) + K_1 (1/T_\ast)\} = nmc^2 \frac{3K_3(1/T_\ast) + K_1(1/T_\ast)}{4K_2(1/T_\ast)} \tag{12}\] \[P = \pi g e^{\frac{\mu}{k_B T}} \left( \frac{mc}{h} \right)^3 k_B T \{ 3K_3(1/T_\ast) - K_1 (1/T_\ast)\} = n k_B T \tag{13}\]のようになります。 途中、修正ベッセル関数の漸化式\(K_{\nu +1} (z)- K_{\nu -1} (z)= \frac{2\nu}{z} K_\nu (z)\)を用いました。 さらにエンタルピー密度が
\[\varepsilon + P = n m c^2 \frac{K_3 (1/T_\ast)}{K_2 (1/T_\ast)} \tag{14}\]のように、簡単な表式となります。 これらにより、状態方程式が定まりましたが、便宜的に
\[P = (\Gamma - 1) (\varepsilon - nmc^2) \tag{15}\]のように書くこともあります。 ここで断熱指数\(\Gamma\)は
\[\Gamma = 1 + \frac{4T_\ast K_2(1/T_\ast)}{3K_3(1/T_\ast) + K_1(1/T_\ast) - 4K_2(1/T_\ast)} \tag{16}\]のようになります。 非相対論的な極限(\(T_\ast \rightarrow 0\))では\(\Gamma = 5/3\)、相対論的な極限(\(T_\ast \rightarrow \infty\))では\(\Gamma = 4/3\)となります。
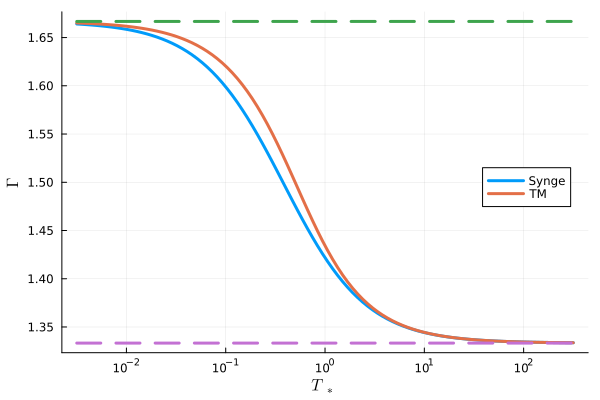
横軸\(T_\ast\)、縦軸\(\Gamma\)としたグラフ。Syngeは(16)式、TMはMathews (1971)で導入されたもの。
(5)式から、1粒子あたりのエントロピーも
\[s = k_B \tag{17}\]のようになります。 非平衡の場合も含め、エントロピー密度は
\[ns = -k_B \int d^3 \mathbf{p} f(\mathbf{p}) \left\{ \ln \left( \frac{h^3 f(\mathbf{p})}{g}\right) -1 \right\} \tag{18}\]とも表されます。
化学平衡
相対論的な温度では、粒子の生成消滅が重要になります。 化学平衡状態では、反応
\[A + B \rightleftharpoons C + D\]に対し、平衡条件
\[\mu_A + \mu_B = \mu_C + \mu_D \tag{19}\]が成立します。 代表的なものとして、電子・陽電子の対生成・対消滅を考えてみましょう。 \(A\)を電子、\(B\)を陽電子、そして\(C, D\)を光子とすると、熱平衡状態での光子の化学ポテンシャルはゼロなので
\[\mu_- + \mu_+ = 0 \tag{20}\]のようになります。 よって縮退が無視できる時には、化学平衡状態では
\[\begin{align} &n_- = 8\pi \left( \frac{mc}{h} \right)^3 e^{\frac{\mu_-}{k_B T}} T_\ast K_2 (1/T_\ast), \quad n_+ = 8\pi \left( \frac{mc}{h} \right)^3 e^{\frac{\mu_+}{k_B T}} T_\ast K_2 (1/T_\ast) = 8\pi \left( \frac{mc}{h} \right)^3 e^{- \frac{\mu_-}{k_B T}} T_\ast K_2 (1/T_\ast) \notag \\ &\Longrightarrow \ n_- n_+ = \left\{ 8\pi T_\ast \left( \frac{mc}{h} \right)^3 K_2 (1/T_\ast) \right\}^2 \tag{21} \end{align}\]のようになります。 ここで陽子数密度\(n_p\)が与えられており、さらに荷電中性条件
\[n_- = n_p + n_+ \tag{22}\]が成立しているとすると、陽電子密度は\(n_p\)と温度\(T\)の関数として与えられます。 相対論的な温度では、(20)式と(10)式より\(n_- n_+ \approx n_\gamma^2\)となります。 陽子数密度が十分小さい\((n_p \ll (k_B T / hc)^3)\)場合には、\(\mu_+ \approx \mu_- \sim 0, n_+ \approx n_- \approx n_\gamma\)のようになります。 このような状態は、宇宙初期に実現されていると言われています。 一方、陽子数密度が十分大きい\((n_p \gg (k_B T / hc)^3)\)場合には、陽電子数密度は\(n_+ \approx n_\gamma^2 / n_p\)の程度となります。 このような状況は、進化した星の高密度コアに対応していますが、星のコアの実際の状況では、電子縮退の効果や陽子の電子捕獲による中性子生成などの過程が支配的となります。
宇宙初期の電子質量を超えるような温度の場合、物質は電磁相互作用だけでなく、弱い相互作用でも平衡状態にあると考えられます。 このときには、光子だけでなくニュートリノも化学平衡状態となり
などの反応を通して、\(\mu_{\bar{\nu}_e} \approx \mu_{\nu_e} \approx \mu_+ \approx \mu_- \sim 0\)となっています。 光ニュートリノ過程やニュートリノ制動放射を通じ、ミューニュートリノとタウニュートリノの対生成も同様に生じます。 そしてニュートリノ振動を通じが混合もあるため、これらも化学平衡状態となり、大量のニュートリノが存在することになります。 さらに高温になると、ミュー粒子も存在するようになります。 さらに温度が高い場合には、反核子も出てくるとされていますが、実際には核子を構成しているクォークの閉じ込めが破れ、クォーク・グルーオンプラズマとなります。 宇宙はこのような高温の熱平衡状態 (ビッグバン)から始まったとされています。 高温の状態で存在したこれら粒子は宇宙膨張とともに、相互作用の時間が長くなっていきます。 そして他の物質と相互作用しなくなり、その後は自由に運動するだけとなります。 これを宇宙初期の残存粒子と呼びますが、光子は現在温度2.7Kの宇宙黒体放射として観測されています。 同様に、ニュートリノも1.9Kの黒体放射として残存していることが予言されていますが、現在の観測技術では検出できていません。
ウィーン平衡
完全な熱平衡状態を達成するためには、エネルギーの変換とともに、粒子の生成消滅反応も起こる必要があります。 考えている系の力学的な時間スケールに対して、生成消滅反応の時間が長いときには、エネルギー交換は十分に起こりますが、粒子数が変化しないという状況も起こり得ます。
宇宙背景放射は、エネルギー交換の時間さえ宇宙の膨張の典型的な時間スケールより長くなっているため、現在の宇宙全体では、宇宙背景放射と通常の物質との間は熱平衡の関係にありません。 よって宇宙が今より千倍も小さかった昔 (\(z \sim 1000\))に熱平衡にあった時期の熱輻射が、背景放射として観測されています。 ニュートリノ背景放射は、温度が約1MeVの時期に熱平衡から切り離されたものとされています。 光子やニュートリノは質量がゼロ(またはゼロに近い)ため、熱平衡から切り離されたときには、完全な熱平衡分布をしています。 熱平衡から切り離された時の温度が質量よりも小さい場合には、その後、化学平衡分布からのずれが出てきます。 一般には粒子反粒子の対消滅により粒子数が減少しますが、反応率が小さいと一定数の粒子が残存することになります。 このときの位相空間分布関数は、化学ポテンシャルが有限の値をもつマクスウェル分布で近似されると考えて良いでしょう (厳密にはボルツマン方程式を解く必要があります。) 宇宙の物質の起源という問題は、現在の宇宙にある核子の数がこのような考察から得られる残存量よりも何十桁も大きいという問題です。 また宇宙の物質密度の大部分を占める暗黒物質は、相互作用が弱いために非常に高い温度で熱平衡から切り離された残存物質である可能性が大きいと考えられています。
X線を放出するようなX線星や活動銀河などに存在する高温のプラズマ中でも類似の現象が起こると考えられています。 この時には、X線放射は制動放射で生じ、コンプトン散乱で物質とエネルギーを交換しながら、吸収される前に外部に脱出します。 このような状況では、光子の分布関数はプランク分布にはなりません。 同じ温度のプランク分布に比べ、著しく少数の光子からなる分布となります。 物質との間でのエネルギー交換が十分素早く起こっているとすると、光子の分布関数は化学ポテンシャルを持ったマクスウェル分布となります。 これをウィーン分布と呼びます。 このプラズマ中での電子陽電子対の生成は、光子光子衝突の断面積が電子散乱と同程度であるため、温度が相対論的になれば十分速いと考えられるでしょう。 従って、化学ポテンシャルを持った光子との化学平衡にある分布とみなすことができます。 この平衡をウィーン平衡と呼びます。
ウィーン平衡では、光子の分布関数もマクスウェル・ボルツマン分布 (ウィーン分布)になるので、その数密度は
のように表されます。 化学平衡の式より
\[\mu_+ + \mu_- = 2\mu_\gamma \tag{24}\]であるため、陽電子の存在量は
\[\frac{n_- n_+}{n_\gamma^2} = \left( \frac{K_2 (1/T_\ast)}{2T_\ast^2}\right)^2 \tag{24}\]のように求まります。 \(n_\gamma\)に応じて\(n_+\)が決定されますが、輻射輸送は\(n_+\)にも依存するため、問題は非線形となります。 実際に計算を行うと、典型的な場合には、\(T_\ast \sim 0.1\)でも多量の電子陽電子対が存在することが判明しています。
参考文献
[1] Mignone & McKinney, 2007, “Equation of state in relativistic magnetohydrodynamics: variable versus constant adiabatic index”
[2] Mathews, 1971, “The Hydromagnetic Free Expansion of a Relativistic Gas”
[3] Synge, 1957, “The Relativistic Gas”
[4] 北島 歓大, 2025, “相対論的流体力学の粒子法的数値計算法の開発及び高速噴流の解析”
[5] 水田晃, “相対論的流体方程式の数値的解法 I”
[6] 高原文郎, “特殊相対論”