1.2 恒星の等級と色

フィルター関数

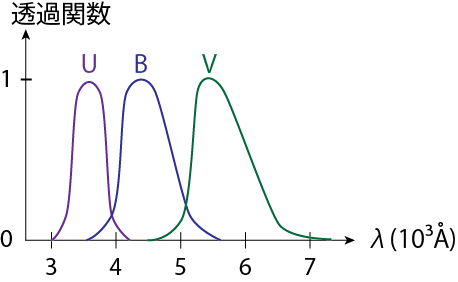
恒星の明るさは、観測する波長によって異なります。観測波長(振動数)域は使用されるフィルターによって決まります。可視光の領域での標準的なフィルターとしてU(Ultraviolet), B(Blue), V(visual)フィルターが用いられます。それぞれのフィルターの透過関数を$\phi_U(\nu), \phi_B(\nu), \phi_V(\nu)$と書くと、それぞれのフィルターを通過するエネルギーは

\[f_U = \int_0^\infty \phi_U(\nu) f_\nu d\nu, \ f_B = \int_0^\infty \phi_B(\nu) f_\nu d\nu, \ f_V = \int_0^\infty \phi_V(\nu) f_\nu d\nu \tag{1.7}\]

のように表されます。

フィルター透過関数

恒星の等級

星の明るさは等級を用いて表されることが多いです。等級は対数的なスケールで、100倍の明るさの違いを5等級の違いとして表します。星1, 2の等級をそれぞれ$m_1, m_2$、そしてそれぞれの星から地上で毎秒受け取るエネルギーを$f_1, f_2$とすると

\[m_2 - m_1 = -2.5 \log(f_2/f_1) \tag{1.8}\]

のように関係づけられます。マイナスの符号は明るい星ほど等級が小さい値を持つという取り決めからきています($f_2/f_1 = 100$のとき$m_2 - m_1 = -5$となります)。見かけの等級システムは、Vega($\alpha$ Lyr)が0等級になるように決められています。よって、UBVフィルターを通して見たときのある星の等級をそれぞれU, B, Vと書くと

\[U = -2.5 \log\left( \frac{f_U}{f_U({\rm Vega})}\right), \ B = -2.5 \log\left( \frac{f_B}{f_B({\rm Vega})}\right), \ V = -2.5 \log\left( \frac{f_V}{f_V({\rm Vega})}\right) \tag{1.9}\]

と表されます。見かけの等級を表すのに小文字の$m$を用いて$m_U, m_B, m_V$と表すこともあります。

前節の(1.3)’式より、同じ固有の明るさ$L$を持っている星でも地球からの距離によって見かけの明るさは変わります。例えば

\[V = -2.5 \log L_V + 5 \log D + {\rm Const.} \tag{1.10}\]

のようになります。そこで、10pcから星を観測したときの等級を絶対等級$M_V$と定義します。この定義に依ると

\[M_V = -2.5 \log L_V + 5 \log (10{\rm pc})+ {\rm Const.} \tag{1.11}\]

です。よって見かけの等級と絶対等級との関係は

\[M_V = V - 5 \log D({\rm pc})＋５ \tag{1.12}\]

となります。ここで$D$(pc)はパーセク(parsec)を単位とした距離を表します。$V-M_V$は距離指数と呼ばれます。

2色図

星からの光は大雑把にいうと、黒体放射に近いです。よって恒星の光球の温度が低いほど、低波長の短い光で見た明るさが暗くなります(このことをより赤く見えると表現されることが多くあります)。異なるフィルターでの等級の差$U-B, B-V$はcolor(色指数)と呼ばれます。これは(1.10)式から明らかなように距離に依存せず、恒星の表面温度の指標として用いられます。

色指数は波長の短い等級から波長の長い等級を引くように決められています。色指数が大きい値を持つほど赤く表面温度が低いことを表します。

太陽の色指数は$U-B=+0.13, B-V=+0.65$です。

先ほど説明した通り、色指数には距離の項はキャンセルされて入っていません。しかし、星間ダストによって短い波長の光が吸収散乱されやすいので、colorは赤化(Interstellar Reddening)されます。

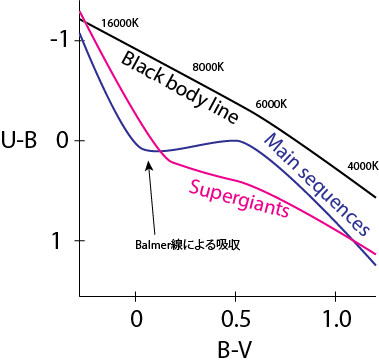
次の図は2色図(color-color diagram)の一例です。縦軸は上に行くほど色指数の値が小さく(色が青く)なるようにとってあります。横軸は右向きに色指数が大きくなるようになっています。通常、波長の短い等級のペアで作成した色指数を縦軸にとります。この時からわかるように、後世からの光は恒星大気で受ける原子・イオンによる吸収により、黒体放射から少しずれています。$B-V \sim 0$で凹んでいるのは、水素のBalmar limit (364.6 nm, or 3646 $\A$)よりも短い波長での吸収の急激な増加、Balmer-jumpの影響です。

2色図

HR図

縦軸に絶対等級、横軸に色指数を取った図が、観測的HR図です。色等級図(color-magnitude diagram)とも呼ばれます。次の図は太陽近傍の恒星のHR図で、主系列星(Main sequence), 巨星(Giants), 超巨星(Supergiants), 白色矮星(White dwarfs)が現れています。

HR図

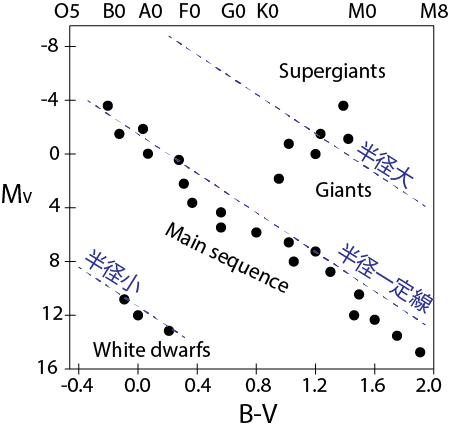
縦軸は上にいくほど明るい
横軸は表面温度を表し、左にいくほど高温。

HR図に表示されている主系列星とは、中心部で4H->Heの核融合反応によりエネルギー供給が行われている恒星のことです。
またHR図の特性から、右上ほど半径が大きくなります。

全放射補正

$M_V$はVフィルターを投下する光のエネルギー量です。しかし高温の恒星は紫外域で、そして低温の恒星は赤外域で多くのエネルギーを放出するので、$M_V$はその星の全波長域でだすエネルギーには対応していません。よってそれを補正するために全放射補正 B.C. が導入されました。このとき全放射(絶対)等級$M_{\rm bol}$が

\[M_{\rm bol} = M_V + {\rm B.C.}\]

のように定義されます。