角径距離

続いて角半距離(Angular diameter distance)を導出しましょう。

見かけの大きさと距離の関係

ユークリッド幾何学においては、大きさが\(y\)の物体が距離\(D_A\)にあるとき、その見かけの大きさを\(d\theta\)とすると

\[y = D_A d\theta\]

の関係にあるので

\[D_A = \frac{y}{d\theta}\]

のように\(d \theta\)を観測で求めればその物体までの距離がわかります。

角径距離の導出

ロバートソン・ウォーカー計量より

\[ds^2 = -c^2 dt^2 +a^2 (\frac{dr^2}{1-Kr^2} + r^2 d\theta^2 + r^2\sin^2 \theta d\varphi)\]

ここに\(dt = dr = d\varphi = 0\)を代入すると

\[ds = ar d\theta\]

この\(ds\)を、先ほどの物体の大きさ\(y\)とすると

\[D_A = a r = \frac{r}{1+z}\]

光度距離は\(D_L = (1+z) r\)より

\[D_A = \frac{D_L}{(1+z)^2}\]

の関係にあることがわかります。

EdS宇宙

特にアインシュタイン・ド・ジッター宇宙のときには

\[D_A = \frac{2c}{H_0} \frac{1}{1+z} (1-\frac{1}{\sqrt{1+z}})\]

となります。

例題: Totally flat model

\(\Omega_{r, 0} = 0, \Omega_{m, 0} + \Omega_{\rm DE, 0} = 1, \Omega_{m, 0} + \Omega_{\Lambda, 0} = 1\)のとき、\(\Omega_{\Lambda, 0} = 1-\Omega_{m, 0}\)より

\[D_A = \frac{c}{H_0} \frac{1}{1+z} \int_0^z \frac{dz}{(\Omega_{m, 0} (1+z)^3 + 1-\Omega_{m, 0})^{1/2}}\]

このモデルでの光度距離を計算するPythonスクリプトとその計算例を掲載します。

#!/usr/bin/env python3 

from scipy import integrate
import numpy as np
import matplotlib.pyplot as plt

# define integrand
def func(omega_m, z):
    return 1 / np.sqrt(omega_m*(1+z)**3+1-omega_m)

if __name__ == '__main__':
    # set variables
    iz = 100
    # set plot range
    zmin = 0.0
    zmax = 5.0
    # set density parameter
    oms = (0.0, 0.3, 1.0)
    # set z coordinate
    zlist = np.linspace(zmin, zmax, iz)
    # set Romberg integrate step
    izz = 1 + 2 ** 6
    # main loop
    for om in oms:
        # set empty list for dl
        dl = []
        # compute [0:z] integration
        for z in zlist:
            zz = np.linspace(0.0, z, izz)
            # compute luminosity distance
            d = integrate.romb(func(om, zz), dx=zz[1]-zz[0]) / (1+z)
            dl.append(d)
        # make plot
        plt.plot(zlist, dl)
    # show plot
    plt.show()

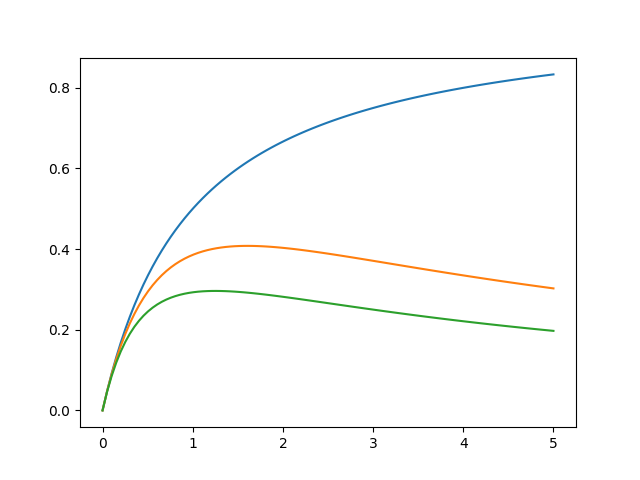
光度距離の作図例

青, オレンジ, 緑線の順に、\(\Omega_{m, 0} = 0, 0.3, 1.0\)のプロット。横軸: 赤方偏移、縦軸: \(D_L/(c/H_0)\)

\(z\)が大きい(宇宙初期)ほど距離が小さい(近くにあるように見える)のは、過去に遡るほど宇宙の大きさが小さくなるため、大きさが同じ天体でも宇宙全体に占める割合が大きくなることに由来しています。