サハの式

サハの電離式の導出

原子の電離度は、サハの式を用いて求めることができます。 LTEでは、\(r\)回電離したイオン\(A_r\)から\(r+1\)回電離したイオン\(A_{r+1}\)への電離とその逆の再結合が平衡にあり

\[A_r \ \longleftrightarrow \ A_{r+1} + \mathrm{e}^- \tag{3.6.1}\]

のように書けます。 \(A_r, A_{r+1}\)および電子の化学ポテンシャルを\(k_B T\)で割った量をそれぞれ\(\eta_r, \eta_{r+1}, \eta_\mathrm{e}\)のように書くことにしましょう。平衡状態では\(\sum_i \eta_i dN_i = 0\)より

\[\eta_{r+1} + \eta_\mathrm{e} - \eta_r = 0 \tag{3.6.2}\]

の関係があります。イオン\(A_r\)とイオン\(A_{r+1}\)および電子の数密度をそれぞれ\(N_r, N_{r+1}, N_\mathrm{e}\)とし、各粒子がマクスウェル・ボルツマン分布に従うとしましょう。すると(3.3.3)式より

\[e^{\eta_r} = \frac{N_r h^3}{z_r (2\pi mk_B T)^{3/2}} e^{\frac{\mathcal{E}_{0, r}}{k_B T}}, \quad e^{\eta_{r+1}} = \frac{N_{r+1} h^3}{z_{r+1} (2\pi mk_B T)^{3/2}} e^{\frac{\mathcal{E}_{0, r+1}}{k_B T}}, \quad e^{\eta_\mathrm{e}} = \frac{N_\mathrm{e} h^3}{2 (2\pi m_\mathrm{e} k_B T)^{3/2}} \tag{3.6.3}\]

が得られます。ここでイオンと電子の質量をそれぞれ\(m, m_e\)とし、電子の内部状態のエネルギーは\(\mathcal{E}_\mathrm{0, e} =0\)としました。さらに電子のスピンの自由度は2であることから、\(z_\mathrm{e}=2\)としました。 (3.6.2)式より

\[\begin{align} &e^{\eta_{r+1} + \eta_e - \eta_r} = 1 \ \Longrightarrow \ \frac{z_r}{2 z_{r+1}} \frac{N_{r+1}}{N_r} e^{\frac{\mathcal{E}_{0, r+1} - \mathcal{E}_{0, r}}{k_B T}} \frac{N_\mathrm{e} h^3}{(2\pi m_e k_B T)^{3/2}} = 1 \notag \\ &\Longrightarrow \ \frac{N_{r+1} N_\mathrm{e}}{N_r} = \frac{2z_{r+1}}{z_r} \frac{(2\pi m_e k_B T)^{3/2}}{h^3} e^{- \frac{\chi_r}{k_B T}} \quad \left( \chi_r \equiv \mathcal{E}_{0, r+1} - \mathcal{E}_{0, r}\right) \tag{3.6.4} \end{align}\]

を得ます。ここで\(\chi_r\)は電離エネルギーを表します。電子数密度\(N_e\)は全ての元素が何回電離であるか、すなわち全ての元素に対する電離度からわかる量であるため、逐次的に求めることが可能です。 (3.6.4)式は電子の数密度\(N_\mathrm{e}\)の代わりに電子の分割\(P_\mathrm{e} = N_\mathrm{e} k_B T\)を用いて

\[\frac{N_{r+1} P_\mathrm{e}}{N_r} = \frac{2z_{r+1}}{z_r} \frac{(2\pi m_e)^{3/2}}{h^3} (k_B T)^{5/2} e^{- \frac{\chi_r}{k_B T}} \tag{3.6.4'}\]

と表すこともできます。

水素のみからなるガス

最も単純な例として、水素ガスの電離を考えましょう。中性水素の数密度を\(N_0\)、電離した水素の数密度を\(N_1\)とすると

\[N \equiv N_0 + N_1 = 一定, \quad N_e = N_1\]

の関係にあることがわかります。水素の電離度を\(y\)を

\[y \equiv \frac{N_1}{N} = \frac{N_\mathrm{e}}{N} = 1 - \frac{N_0}{N} \quad (0 \leq y \leq 1) \tag{3.6.6}\]

のように定義しましょう。 \(N_0, N_1, N_\mathrm{e}\)を\(y, N\)で表すことで、水素の電離に対するサハの式(3.6.4)を書くことにすると

\[\frac{N_1 N_\mathrm{e}}{N_0} = \frac{N_1^2}{N_0} = \frac{y^2}{1-y} \frac{2z_1}{Nz_0} \left( \frac{2\pi m_\mathrm{e} k_B T}{h^2}\right)^{3/2} e^{-\frac{\chi_\mathrm{H}}{k_B T}} \tag{3.6.7}\]

のようになります。中性水素において、その基底状態のみを考えることにすると、その統計的重率は\(z_0 = 2\)となります。それに対し電離した水素は電子を持たないため、\(z_1 = 1\)tとなります。水素の電離エネルギーは\(13.6 \mathrm{eV} = 2.179 \times 10^{-11} \mathrm{erg}\)より

\[\frac{\chi_\mathrm{H}}{k_B T} \simeq \frac{1.578 \times 10^5}{T}\]

となります。また\(N = \rho / m_p\)であることを代入すると、(3.6.7)式は

\[\frac{y^2}{1-y} = 4.01 \times 10^{-9} \frac{T^{3/2}}{\rho} e^{-\frac{1.578 \times 10^5}{T}} \tag{3.6.8}\]

のようになります。左辺は\(0 \leq y < 1\)で単調増加関数なので、右辺が大きいほど電離度が大きいとわかります。ある温度に対する電離度は、密度が大きいほど低くなることがわかります。しかし、その依存性は弱く、電離度は指数関数の中にある温度\(T\)に対して敏感であることがわかります。
(3.6.8)式の両辺に\(1-y\)をかければ、これは\(y\)についての二次方程式となります。すると解の公式を用いることで、水素ガスの電離度\(0 \leq y \leq 1\)を求めることができます。横軸をガスの温度、縦軸を電離度として図示したものが下のグラフです。

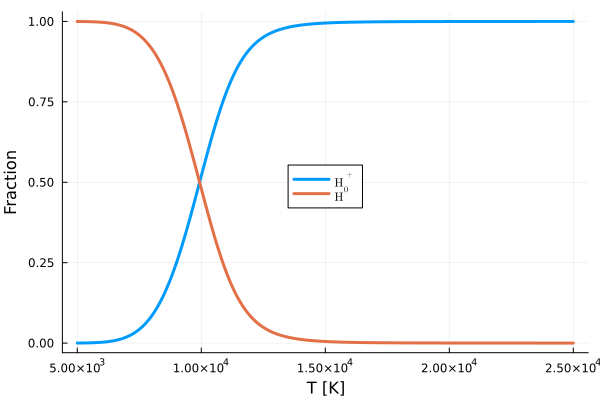
ここではガスの質量密度を\(\rho = 10^{-9} \mathrm{g \ cm^{-3}}\)としました。これはA0星の光球面での典型的な値として知られています。またA0星の表面温度はおよそ\(10^4\)K程度であることから、この温度では中性水素が半分程度残っていることがわかります。

ヘリウムのみからなるガス

ヘリウムのみからなるガスについても、電離度を求めてみましょう。ただしヘリウムの電離には\(\mathrm{He}^+\)と\(\mathrm{He}^{++}\)があるため、注意が必要です。サハの式より

\[\frac{N_\mathrm{He^+} N_\mathrm{e}}{N_\mathrm{He^0}} = \frac{2 z_\mathrm{He^+}}{z_\mathrm{He^0}} \left( \frac{2\pi m_e k_B T}{h^2} \right)^{3/2} e^{-\frac{\chi_\mathrm{He^0}}{k_B T}} \equiv c_+ \tag{3.6.9}\] \[\frac{N_\mathrm{He^{++}} N_\mathrm{e}}{N_\mathrm{He^+}} = \frac{2 z_\mathrm{He^{++}}}{z_\mathrm{He^+}} \left( \frac{2\pi m_e k_B T}{h^2} \right)^{3/2} e^{-\frac{\chi_\mathrm{He^+}}{k_B T}} \equiv c_{++} \tag{3.6.10}\]

の関係にあることがわかります。また電子数密度は

\[N_\mathrm{e} = N_\mathrm{He^+} + 2 N_\mathrm{He^{++}} \tag{3.6.11}\]

であり、全ヘリウム原子の粒子数は

\[N_\mathrm{He} = N_\mathrm{He^0} + N_\mathrm{He^+} + N_\mathrm{He^{++}} \tag{3.6.12}\]

のように表されます。電離度を求めるために、以下の変数をさらに定義しておきましょう。

\[y \equiv \frac{N_\mathrm{He^+}}{N_\mathrm{He}}, \quad z \equiv \frac{N_\mathrm{He^{++}}}{N_\mathrm{He}} \tag{3.6.13}\]

(3.6.9), (3.6.11), (3.6.12)式より

\[\begin{align} &\frac{N_\mathrm{He^+} (N_\mathrm{He^+} + 2N_\mathrm{He^{++}})}{N_\mathrm{He} - N_\mathrm{He^{+}} - N_\mathrm{He^{++}}} = c_+ \ \Longrightarrow \ N_\mathrm{He^{+}}^2 + 2 N_\mathrm{He^{++}} N_\mathrm{He^{+}} = c_+ (N_\mathrm{He} - N_\mathrm{He^{+}} - N_\mathrm{He^{++}}) \notag \\ &\underbrace{\Longrightarrow}_{\times 1/N_\mathrm{He}^2} \ y^2 + 2z y = c_{+}' (1-y - z) \tag{3.6.14} \end{align}\]

を得ます。途中、\(c_{+}' = c_+ / N_\mathrm{He}\)とおきました。そして(3.6.10)式から

\[\frac{N_\mathrm{He^{++}} (N_\mathrm{He^{+}} + 2 N_\mathrm{He^{++}})}{N_\mathrm{He^{+}}} = c_{++} \ \Longrightarrow \ N_\mathrm{He^{+}} = \frac{2 N_\mathrm{He^{++}}^2}{c_{++} - N_\mathrm{He^{++}}} \ \underbrace{\Longrightarrow}_{\times 1/N_\mathrm{He}} \ y = \frac{2z^2}{c_{++}' - z} \tag{3.6.15}\]

の関係式がわかります。ここでも\(c_{++}' = c_{++} / N_\mathrm{He}\)としました。これを(3.6.14)式に代入すれば

\[\begin{align} &\left( \frac{2z^2}{c_{++}' - z} \right)^2 + 2z \frac{2z^2}{c_{++}' - z} = c_+'\left( 1- \frac{2z^2}{c_{++}' - z} - z \right) = c_+' \frac{c_{++}'- z - z^2 - c_{++}'z}{c_{++}' - z} \notag \\ &\underbrace{\Longrightarrow}_{\times (c_{++}'-z)^2} \ 4z^4 + 4z^3 (c_{++}'-z) = c_{+}' (c_{++}'-z-z^2 - c_{++}'z) (c_{++}'-z) \notag \\ & \qquad \qquad \qquad = c_{+}' (c_{++}'^2 - c_{++}' z - c_{++}' z + z^2 - c_{++}' z^2 + z^3 - c_{++}'^2 z + c_{++}' z^2) \notag \\ & \Longrightarrow \ (4c_{++}' - c_{+}') z^3 - c_{+}' z^2 + (2 + c_{++}') c_{+}' c_{++}' z - c_{+}'c_{++}'^2 = 0 \tag{3.6.16} \end{align}\]

(3.6.16)式は\(z\)の三次関数です。解析的に求めるには三次方程式の解の公式を、数値的に求めるにはニュートン法などを用いることで、\(0\leq z \leq 1\)の解を求めます。そのようにして求まった\(z\)を(3.6.15)式に代入すれば、\(y\)も求めることができます。さらに(3.6.12)式の両辺を\(N_\mathrm{He}\)で割ったものから、\(N_\mathrm{He^0}/ N_\mathrm{He} = 1-y-z\)の関係にあるため、中性ヘリウムの量も計算ができます。

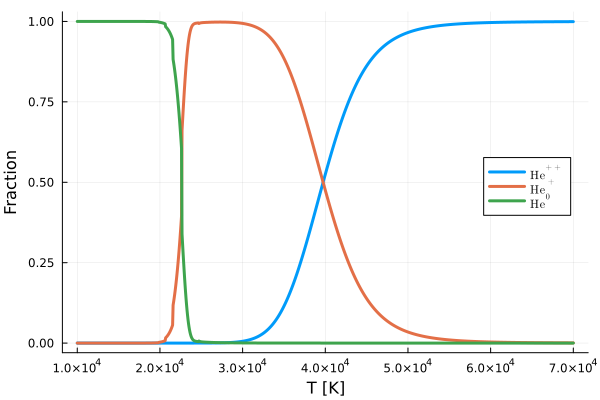
ここではヘリウムガスの質量密度を\(\rho = 10^{-8} \mathrm{g \ cm^{-3}}\)、電離エネルギーを\(\chi_\mathrm{He^0} = 24.587 \mathrm{eV}, \chi_\mathrm{He^+} = 54.416 \mathrm{eV}\)とし、さらにヘリウム原子とイオンの分配関数はそれぞれ\(z_\mathrm{He^0} = 1, z_\mathrm{He^+} = 2, z_\mathrm{He^{++}} = 1\)としました。 \(2 \times 10^4\)Kで\(\mathrm{He}^+\)が増え始めます。さらに温度が上昇すると、\(\mathrm{He}^+ \rightarrow \mathrm{He}^{++} + \mathrm{e}^-\)が起き、\(\mathrm{He}^{++}\)が多くなっていきます。

少し数値振動みたいなものが見られる...数値計算コードのミス？桁落ち？