Table of contents
対流
ガスの流れが発生しない限り、恒星内部でのエネルギーは輻射と熱伝導により運ばれます。 ガスの不透明度が大きい場合、あるエネルギー流束を輻射と熱伝導で運ぶには、大きな温度勾配が必要となります。 しかし温度勾配の大きさがある臨界値を越えると対流が発生し、エネルギー流束の大部分を対流が担うようになります。
対流の発生
まずは対流の発生について考えましょう。 恒星中のガス塊が、揺らぎによって微小距離\(dr\)だけ上昇したとします。 ガス塊内部の物理量には添字\(i\)をつけて表し、ガス塊の内外を問わず元の位置から\(dr\)上昇した場所での物理量には\(\ast\)をつけて表すことにします。 上昇を始める位置、すなわちガス塊が生まれた位置では、ガス塊の内部と外部の温度・密度・圧力は同じであったとします。 またガス塊は常に周囲と圧力平衡を保ちながら上昇、すなわち\(P_i = P, P_i^\ast = P^\ast\)が成り立っていると仮定します。
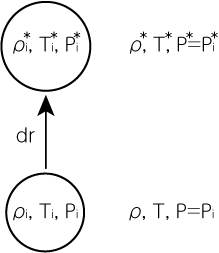
微小距離\(dr\)だけ上昇したとき、ガス塊内部と外部の密度差は
\[\rho_i^\ast - \rho^\ast = \left( \frac{\partial \rho}{\partial T} \right)_P (T_i^\ast - T^\ast) = \left( \frac{\partial \rho}{\partial T} \right)_P \left( \frac{dT_i}{dP} - \frac{dT}{dP} \right) \frac{dP}{dr} dr \tag{5.4.1}\]のように書けます。 ガス塊内の密度の方が大きい(\(\rho_i^\ast > \rho^\ast\))の場合、ガス塊に負の圧力が働き、元の位置に戻ります。 この場合、ガスの構造は安定です。 逆に上昇したガス塊内の密度の方が小さい(\(\rho_i^\ast < \rho^\ast\))とき、ガス塊に浮力が働くため、さらに上昇するガスの運動が発生します。 これは対流が発生することを意味します。 恒星内部では\(\left( \frac{\partial \rho}{\partial T}\right)_P < 0, \frac{dP}{dr}<0\)であるため、(5.4.1)式は
\[\frac{dT_i}{dP} < \frac{dT}{dP} \tag{5.4.2}\]のときに対流が発生することを示しています。
一般に熱の交換に要する時間は力学的時間スケールに比べて非常に長いため、ガス塊の運動は断熱的に起こると近似できます。 すなわち\(\frac{dT_i}{dP} \approx \left( \frac{dT}{dP} \right)_\mathrm{ad}\)と書けます。 ここで、添字のadは断熱変化を表します。 したがって
のとき、つまり温度勾配が断熱的温度勾配により急なときに対流が発生することになります。
輻射(と熱伝導)だけでエネルギーが運ばれると仮定したときに予想される温度勾配に添字radをつけて表すと、(5.3.3)式より
のように表されます。 ここで、この\(\kappa\)には熱伝導の効果が入っているものとします。 恒星の内部構造の記述には、しばしば圧力に対する対数的温度勾配
\[\nabla_\mathrm{rad} \equiv \left( \frac{d \ln T}{d \ln P}\right)_\mathrm{rad} = \frac{P}{T} \frac{3\kappa L_\mathrm{rad}}{16 \pi G M_r a c T^3} = \frac{\kappa L_\mathrm{rad}}{16 \pi G M_r c (1-\beta)}, \quad \nabla_\mathrm{ad} \equiv \left( \frac{d \ln T}{d \ln P}\right)_\mathrm{ad} \tag{5.4.5}\]が用いられます。 ここで、\(\beta\)はガス圧と全圧に対する比 \(P_\mathrm{gas} / P\)で定義され
\[1-\beta = \frac{P_\mathrm{rad}}{P} = \frac{aT^4}{3P} \tag{5.4.6}\]の関係が成り立ちます。 これらを用いると、対流の発生条件(5.4.3)式は
\[\nabla_\mathrm{rad} > \nabla_\mathrm{ad} \tag{5.4.7}\]と書けます。 (5.4.5)式から、不透明度\(\kappa\)が大きいほど、また\(\frac{L_\mathrm{rad}}{M_r (1-\beta)}\)が大きいほど、対流が発生しやすいことがわかります。 前者の条件は、低質量主系列星や赤色巨星の外層で対流が起こる原因(比較的低温のため不透明度が大きい)であり、後者の条件は大質量星の中心部で対流が起こる原因となります。
対流が発生すると、エネルギー輸送は輻射・電子熱伝導および対流によって行われるようになります。 対流によるエネルギー流束を\(F_\mathrm{conv}\)と書くと、対流層内でのエネルギーの流れは
のように表されます。 対流はエネルギーを効率よく運ぶとともに、ガスの混合を行います。 そのため、対流が起こっている流域の元素組成を均一にする効果も持ちます。
理想気体の場合
理想気体では、断熱変化に対して
\[P \propto \rho^\gamma \propto \left( \frac{P}{T}\right)^\gamma \ \Longrightarrow \ T \propto P^{\frac{\gamma - 1}{\gamma}}\]となります。 単原子分子のとき\(\gamma = 5/3\)なので
\[\nabla_\mathrm{ad} = \frac{\gamma - 1}{\gamma} = \frac{2}{5} = 0.4\]となります。
対流によるエネルギー輸送
恒星内で起こる対流はスケールが大きいため、高レイノルズ数の乱流状態となっています。 恒星中での乱流に対する私たちの知識はまだ不十分で、恒星中の対流の物理状態を正確に記述する理論は、現在のところ存在しません。 そのため現在でも多くの場合、1940年代に導入された混合距離理論モデル (mixing length theory)という単純なモデル(もしくはそこから派生したモデル)に基づいて、対流による熱の輸送を計算します。 混合距離理論モデルでは、周囲よりわずかに温度の高いガス塊 (eddyまたはblob)と混合距離\(\ell\)だけ上昇した後、周りのガスと混ざり合います。 そして、その塊が持っていたエネルギー超過を周囲に解放します。 逆に周囲よりわずかに温度の低いガス塊は、混合距離\(\ell\)だけ下降した後、周囲のガスと混ざり合います。 したがって、上昇・下降どちらの場合も、エネルギーは内側から外側の方向に運ばれます。
恒星中心からの距離が\(r\)の球面を考えましょう。 その面を通過する、対流によって運ばれるエネルギー流束 (単位時間・単位面積あたりに通過するエネルギー)は
のように表されます。 ここで\(C_p\)は等圧比熱、\(v\)はガス塊の速度、そして\(\Delta T\)はガス塊と周囲との温度差を表します。 また\(\overline{v \Delta T}\)は\(v \Delta T\)の平均値を表します。 ガス塊は周囲と圧力平衡を保ちながら(すなわち亜音速で)移動すると仮定するため、等圧比熱と温度超過の積により単位質量あたりの熱エネルギー超過を得ることができます。
ガス塊中の温度と周囲との温度差\(\Delta T\)は、ガス塊中での温度勾配\(\left( \frac{dT}{dr}\right)_i\)と周囲の温度勾配\(\frac{dT}{dr}\)との差から生じます。 ガス塊が移動する間に行われる周囲との熱の交換は、表面近くで起こる対流では無視できません。 そのため、実際のモデル計算ではその効果が考慮されます。 しかしここでは議論を簡単にするため、熱の交換はないとしましょう。 ガス塊中の温度は断熱的に変化するとして
とします。 この断熱近似のもとでは、ガス塊の移動に伴う内部の温度超過\(\Delta T\)の変化は
\[\frac{d\Delta T}{dr} \approx \left\{ \left( \frac{dT}{dr} \right)_\mathrm{ad} -\left( \frac{dT}{dr} \right) \right\} = ( \nabla_\mathrm{T} - \nabla_\mathrm{ad} ) \frac{T}{H_p} \tag{5.5.3}\]を得ます。 ここで用いた対流層中での圧力に対する対数温度勾配\(\nabla_\mathrm{T}\)と、圧力変化に対する距離スケール(pressure scale height) \(H_p\)は
\[\nabla_\mathrm{T} \equiv \frac{d \ln T}{d \ln P}, \quad H_p \equiv - \frac{dr}{d \ln P} = \frac{P}{\rho g} \tag{5.5.4}\]のように定義されます。 さらに\(g\)はその位置での重力加速度 \(g = \frac{GM}{r^2}\)を表します。
ガス塊は周囲と圧力平衡にあるため、温度差\(\Delta T\)に相当する密度差は
です。 \(\left( \frac{\partial \rho}{\partial T}\right)_p < 0\)なので、周囲よりも温度が高い場合は密度が低く、浮力\(-g \Delta \rho\)が働くことで上向きに加速されます。 ガス塊に対する運動方程式は
\[\rho \frac{dv}{dt} = -g \Delta \rho = -g \left( \frac{\partial \rho}{\partial T}\right)_p (\nabla_\mathrm{T} - \nabla_\mathrm{ad}) \frac{T \Delta r}{H_p} \tag{5.5.5}\]のように書くことができます。 ここで\(\Delta r\)は、ガス塊が発生してから移動した距離を表します。 (5.5.5)式の両辺に\(v = \frac{d\Delta r}{dt}\)をかけて、式変形を行いましょう。
\[\rho v \frac{dv}{dt} = - g \left( \frac{\partial \rho}{\partial T}\right)_p (\nabla_\mathrm{T} - \nabla_\mathrm{ad}) \frac{T}{H_p} \frac{d\Delta r}{dt} \Delta r \ \underbrace{\Longrightarrow}_{両辺積分} \ v^2 \simeq - g \left( \frac{\partial \ln \rho}{\partial \ln T}\right)_p (\nabla_\mathrm{T} - \nabla_\mathrm{ad}) \frac{\Delta r^2}{H_p}\]途中の積分において、移動距離\(\Delta r\)は十分小さく、このガス塊の移動程度では大きく変化しないと仮定しました。 これで式変形は終わりですが、ガス塊が移動する際に約半分のエネルギーが、周囲のガスを押し除けるのに使われることを考慮して、適当に\(1/2\)をつけて
\[v^2 \simeq \frac{1}{2} g \delta (\nabla_\mathrm{T} - \nabla_\mathrm{ad}) \frac{\Delta r^2}{H_p} \tag{5.5.6}\]のように書くことにします。 ここで
\[\delta \equiv - \left( \frac{\partial \ln \rho}{\partial \ln T}\right)_p \tag{5.5.7}\]は、定圧膨張率を表します。
ある面を通過するガス塊が、生まれてから移動した平均距離\(\overline{\Delta r}\)が混合距離\(\ell\)の半分程度であるとすると
となります。 従って、対流によるエネルギー流束 \(F_\mathrm{conv}\)は、(5.5.1)式で
\[\overline{v \Delta T} \approx \sqrt{\overline{v^2}} \ \overline{\Delta T} \tag{5.5.9}\]のように近似を行うと、(5.5.8)式より
\[F_\mathrm{conv} \simeq \frac{\rho C_p T}{4\sqrt{2}} \sqrt{\delta \frac{P}{\rho}} (\nabla_\mathrm{T} - \nabla_\mathrm{ad})^{3/2} \left( \frac{\ell}{H_p} \right)^2 \tag{5.5.10}\]と表すことができます。 この式から、対流によるエネルギー流束は、混合距離と圧力変化のスケールの長さとの比 \(\ell / H_p\)がパラメータとなっています。 \(\ell / H_p\)に適当な値を与え、さらに上式を(5.4.8)式に用いれば、対流層内での温度勾配を求めることができます。 例として、これを太陽の対流層に適用してみましょう。 簡単のため、完全電離した水素からなる理想気体(\(\delta = 1\))を想定し、さらに簡単のために\(\ell \sim H_p\)としてみます。 このとき
\[L_{r, \mathrm{conv}} = 4\pi r^2 F_\mathrm{conv} \simeq 1.2 \times 10^{12} r^2 \rho T^{3/2} (\nabla_\mathrm{T} - \nabla_\mathrm{ad})^{3/2}\]を得ます。 太陽対流層の比較的内側の部分での状態 \(\rho \sim 1 \mathrm{g/cm^3}, T \sim 10^6 \mathrm{K}, r \sim 10^{10} \mathrm{cm}\)を用いると
\[L_{r, \mathrm{conv}} \simeq 10^{41} (\nabla_\mathrm{T} - \nabla_\mathrm{ad})^{3/2} \ [\mathrm{erg/s}]\]のようになります。 従って、太陽表面から出るエネルギー\(\sim 4 \times 10^{33} \mathrm{erg/s}\)を対流で運ぶのに必要な温度勾配は、\(\nabla_\mathrm{T} - \nabla_\mathrm{ad} \simeq 10^{-6}\)となります。 すなわち、対流層深部では温度勾配は良い近似で断熱的な温度勾配となっています。 このことは、内部では対流による熱輸送の効率が非常に良いことを示しています。 状態方程式が理想気体の場合、このような場所の構造は\(n = 3/2 \ (P \propto \rho^{5/2})\)のポリトロープとなっていることも知られています。
表面に非常に近い場所では、ガスの密度が小さいために対流の熱輸送効率は十分でなく、比較的大きな\(\nabla_\mathrm{T} - \nabla_\mathrm{ad}\) (super-adiabatic temperature gradient: 超断熱的温度勾配)が生じます。 \(\nabla_\mathrm{T} - \nabla_\mathrm{ad}\)が大きな層でのその値の大きさは、仮定された混合距離の大きさに依存し、そして恒星半径にも影響を及ぼします。 そのため、表面温度が低く対流外層を持つような構成に対する構造モデルの半径は、仮定された混合距離の値に依存し、一意に決定されません。 観測との比較に使われるモデルを計算する際には、\(1M_\odot\)の質量を持つモデルが、46億年進化した場合に太陽半径と太陽光度を持つように、混合距離と圧力変化の距離スケールとの比 \(\ell / H_p\)の値を決定します。 そしてその値を他の質量を持つモデルについても適用する、ということが多くあります。
しかし、\(\ell / H_p\)の値が対流層の中で一定となるという保障はありません。 そして太陽と異なる構造を持つ恒星に対して、太陽で校正した値が適当であるということも確証はありません。 対流の取り扱いは恒星の内部構造理論のうちで、最も不確定な要素の一つと言えるでしょう。
参考文献
[1] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[2] 高原文郎, “宇宙物理学”
[3] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”