Table of contents
  1. Rusanov法
    1. 流束計算
    2. Rusanov流束の計算モジュール

Rusanov法

ここでは(磁気)流体力学の計算手法であるRusanov法についての勉強メモを記述しています。

流束計算

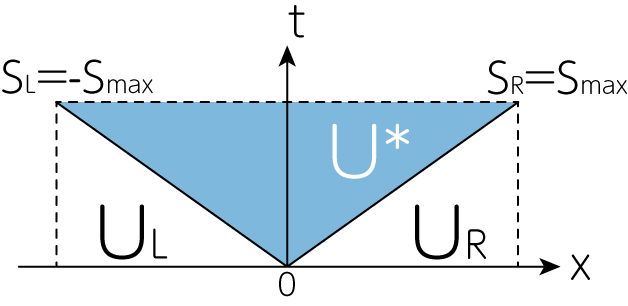
実はとても簡単です。HLL法において、\(S_R = S_\mathrm{max}, S_L = -S_\mathrm{max}\)のようにしたものがRusanov流束になります。すなわち

\[\mathbf{F}^\ast = \frac{S_\mathrm{max} \mathbf{F}_L + S_\mathrm{max} \mathbf{F}_R - S_\mathrm{max}^2 (\mathbf{U}_R - \mathbf{U}_L)}{2 S_\mathrm{max}} = \frac{1}{2} \left\{ \mathbf{F}_R + \mathbf{F}_L - S_\mathrm{max} (\mathbf{U}_R - \mathbf{U}_L)\right\}\tag{1}\]

左側と右側の流束を平均したような形になります。これは\(S_R = -S_L\)としていることからわかるように、左側に進む波と右側に進む波の速度を区別しません。これにより流束計算が非常に簡単かつ、実際に数値計算をした際にも高速に実行することができます。

もちろん欠点も存在します。その流束計算方法から、左右どちらかに進行する速進衝撃波は捉えることができますが、それ以外の構造は捉えることができません。すなわち接触不連続面などは上手に分解できず、鈍った結果となります。

複雑な流体構造により計算が停止するような場合には、まずRusanov法などの解像度の低い手法を試してみると良いかも？
とりあえず計算が途中で停止せず、動かせはするはずです。

Rusanov流束の計算モジュール

以下にRusanov流束計算コードのJulia実装例を示します。

using LinearAlgebra    
include("../convert/convert.jl")
include("../const/const.jl")
function hll!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64)
    for i in 1:nxmax-1
        # compute B * B of left side
        bl2 = dot(Vl[6:8, i], Vl[6:8, i])
        # compute v * B of left side
        vlbl = dot(Vl[2:4, i], Vl[6:8, i])
        # convert Vl ---> Ul
        Ul = Convert.v_to_u(Vl[:, i])
        # convert Ul, VL ---> Fl
        Fl = Convert.uv_to_f(Ul, Vl[:, i], bl2, vlbl)
        # compute fast-mode speed of left side
        gmprl = gm * Vl[5, i]
        vfl = sqrt(((bl2+gmprl)+sqrt((bl2+gmprl)^2-4*gmprl*Vl[6, i]^2))/(2*Vl[1, i]))
        # compute B * B of right side
        br2 = dot(Vr[6:8, i], Vr[6:8, i])
        # compute v * B of right side
        vrbr = dot(Vr[2:4, i], Vr[6:8, i])
        # convert Vr ---> Ur
        Ur = Convert.v_to_u(Vr[:, i])
        # convert Ur, Vr ---> Fr
        Fr = Convert.uv_to_f(Ur, Vr[:, i], br2, vrbr)
        # compute fast-mode speed of right side
        gmprr = gm * Vr[5, i]
        vfr = sqrt(((br2+gmprr)+sqrt((br2+gmprr)^2-4*gmprr*Vr[6, i]^2))/(2*Vr[1, i]))
        # compute smax
        smax = max(Vl[2, i], Vr[2, i])+max(vfl, vfr)
        # compute Rusanov flux
        for m in 1:8
            F[m, i] = 0.5 * (Fr[m]+Fl[m]-smax*(Ur[m]-Ul[m]))
        end
    end
end

HLLの計算方法と特に変わりはありません。

Copyright © github-nakasho