Table of contents
白色矮星の進化
ここでは、白色矮星の(冷却)進化についてメモしています。
概要
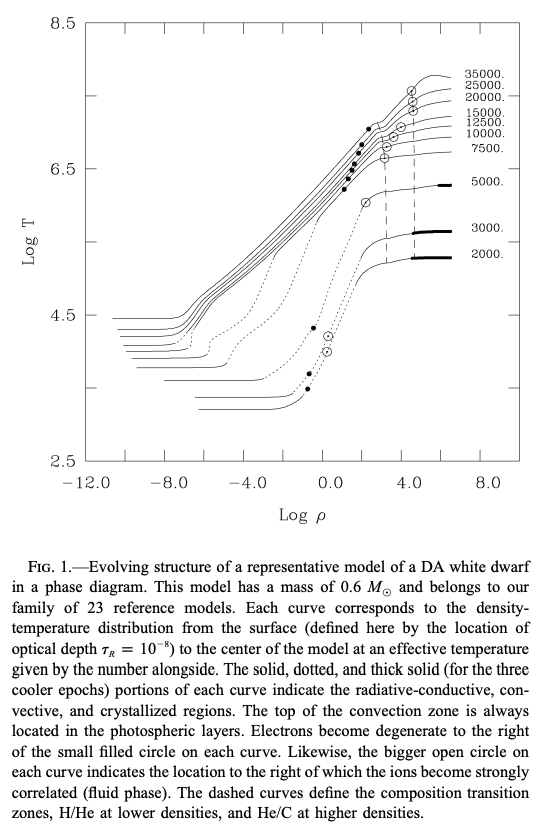
次の図は、\(0.6 M_\odot\)のDA型白色矮星のモデル内部の密度-温度関係を、異なる進化段階に対して表したものです。
各線の右に記された有効温度の低いモデルほど、進化 (冷却) の進んだモデルとなっています。 点線の部分は対流層を表し、黒丸より内側の部分では電子が縮退しています。 また白丸より内側では物質が液体の状態になっており、さらに太い実践部分は結晶化された層を表しています。 進化が進につれ、有効温度と内部温度が下がっていき、縮退領域が表面に近づいていきます。 さらに十分に進化が進んだ段階では、中心部が固体となります (crystallization。) 液体から固体への遷移は、臨界クーロンパラメータ (critical Coulomb parameter)
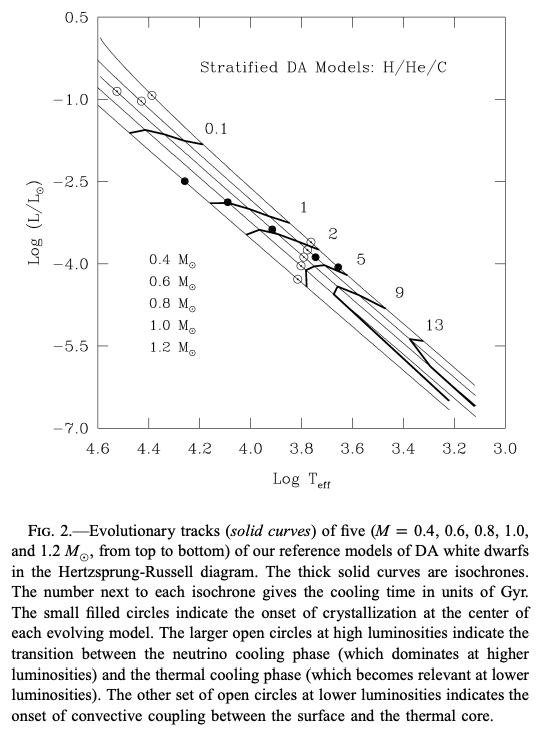
\[\Gamma = \frac{Z^2 e^2}{a k_B T} = 170 \sim 200\]のときに起こります。 ここで\(a\)は、イオン間の平均距離です。 この遷移は一次相転移で、潜熱が発生します。 そして結晶化が起こると、自由度が減少し比熱が小さくなるため、冷却率 (cooling rate)が大きくなります。 次の図は、HR図上の各質量の白色矮星の進化経路と、太い実戦は等時曲線 (isochrone)を示したものです。
進化は左上から右下へと進みます。 質量の大きい白色矮星ほど半径が小さいため、左下の線ほど質量の大きな白色矮星の進化経路に対応します。 各進化経路において、最初の白丸部分までは光の光度よりもニュートリノ光度の方が大きくなっています。 また二番目の白丸より下では、対流層が等温中心核の境界まで達している状態を表しています。 また黒丸は結晶化が始まる時点を表しています。 質量の大きい白色矮星ほど密度が大きいため、進化の早い段階 (中心温度の高い段階)で中心核の結晶化が始まり、進化スピードが速くなります。 このことは、大きい年齢に対する等時曲線が、質量の大きい側で大きく曲がっていることに現れています。
簡単なモデルでの冷却率の評価
ここでは非常に簡単なモデルを仮定し、白色矮星の冷却率を解析的に求めてみましょう。 白色矮星を、等温かつ縮退した中心核と、非常に薄い理想気体で輻射平衡にある外層とで構成されているとします。
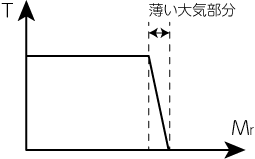
この2つの層の境界の温度と密度を、それぞれ\(T_\ast, \rho_\ast\)と書くことにします。
輻射平衡の外挿に対しては、\(M_r \simeq M, L_r \simeq L\)として
が成り立ちます。 (2)式を(1)式で割ると
\[\frac{dP}{dT} = \frac{4ac T^3}{3\kappa} \frac{4\pi GM}{L} \tag{3}\]を得ます。 クラマース型の不透明度と理想気体の関係式
\[\kappa = \kappa_0 \rho T^{-3.5}, \quad P = \frac{N_\mathrm{A} k_B}{\mu} \rho T \tag{4}\]を、(3)式に代入しましょう。 \(\kappa, \rho\)を消去すると
\[\frac{dP}{dT} = \frac{16 \pi a c G}{3\kappa_0} \frac{N_\mathrm{A} k_B}{\mu} \frac{M T^{7.5}}{L P} \tag{5}\]となります。 この式を積分しましょう。 表面で\(P=0\)という条件から、積分定数を定めることにしましょう。 すると
\[\begin{align} &\int P dP = \frac{16 \pi a c G}{3\kappa_0} \frac{N_\mathrm{A} k_B}{\mu} \frac{M}{L} \int T^{7.5} dT \ \Longrightarrow \ \frac{1}{2} P^2 = \frac{16 \pi a c G}{3\kappa_0} \frac{N_\mathrm{A} k_B}{\mu} \frac{M}{L} \frac{T^{8.5}}{8.5} \notag \\ & \Longrightarrow \ P \propto \sqrt{\frac{M}{L}} T^{4.25} \tag{6} \end{align}\]を得ます。 ここに理想気体の状態方程式 (4)を用いれば
\[\rho \propto \sqrt{\frac{M}{L}} T^{3.25} \tag{7}\]となります。
一方、縮退した白色矮星内部において、相対論的効果を無視すると\(P \propto \rho^{5/3}\)という関係があります。 縮退内部と外層の境界では、この関係と(6), (7)式の関係が共に成り立っているはずなので
の関係が得られます。 これを変形すると
\[L \propto M T_\ast^{7/2} \tag{9}\]を得ます。 これは、白色矮星の内部温度が下がるにつれて、光度\(L\)が減少することを示しています。 係数をしっかり計算すると、この関係は
\[\frac{L}{L_\odot} \simeq 6.6 \times 10^{-29} \mu T^{7/2}\frac{M}{M_\odot} \tag{9'}\]と表されます。 ここで外層のほとんどがヘリウムと炭素から成り立っているとすると\(\mu \sim 2\)であり、さらに典型的な白色矮星の質量として\(M \sim 0.6 M_\odot\)としましょう。 以上から
\[T_\ast = 10^8 \ [\mathrm{K}] \ \longleftrightarrow \ L \simeq 0.8 L_\odot, \quad T_\ast = 10^7 \ [\mathrm{K}] \ \longleftrightarrow \ L \simeq 2.5 \times 10^{-4} L_\odot \tag{10}\]のような、内部温度と明るさの対応が得られます。
白色矮星からの星の光として放出されるエネルギーの源は、原子核(理想気体として扱えるとします)の熱運動エネルギーです (縮退した電子は密度のみで決まるエネルギーを持ち、取り出すことはできません。) 原子核の熱運動のエネルギーは
と表されます。 ここで、\(A\)は白色矮星を構成している原子核の質量数です。 白色矮星の光度は、\(E_\mathrm{I}\)の減少率に等しいため
\[L = - \frac{dE_\mathrm{I}}{dt} = - \frac{3}{2} N_\mathrm{A} \frac{k_B M}{A} \frac{T_\ast}{dt} \tag{12}\]これを(9’)式に代入すると
\[\frac{dT_\ast}{dt} \simeq -1.06 \times 10^{-36} A \mu T_\ast^{3.5} \tag{13}\]の関係が得られます。 この式は、冷却率が内部温度の減少に伴って小さくなっていくことを表しています。 この式を、\(t=t_0\)で\(T_\ast = T_0\)という初期条件のもとで積分しましょう。 すると
\[T_\ast^{-2.5} - T_0^{-2.5} \simeq 2.6 \times 10^{-36} A \mu (t-t_0) \tag{14}\]となります。 冷却時間を\(\tau \equiv t - t_0\)と定義し、\(T_0 \gg T_\ast\)であることを用いると、この式から
\[\tau \simeq \frac{1.2 \times 10^{28}}{A \mu} T_\ast^{-5/2} \ [\mathrm{yr}] \tag{15}\]のようになります。 さらに(9’)式を用いると
\[\tau \simeq 8.8 \times 10^6 \left( \frac{A}{12}\right)^{-1} \left( \frac{\mu}{2}\right)^{-2/7} \left( \frac{M/M_\odot}{L/L_\odot}\right)^{5/7} \ [\mathrm{yr}] \tag{16}\]を得ます。 この式の最初の係数は、詳しいモデル計算の結果と一致するように、解析的に求まる値から40%程度大きくしたものを用いました (もとの値は\(6.3 \times 10^6\)。) これは、冷却時間は光度が下がるほど長くなり、また白色矮星を構成する原子核の質量数が大きいほど短いことを表しています。 後者の性質は、同じ質量の白色矮星を構成する場合に原子核数が少なくなるために、ある温度に対する星全体の熱エネルギーが少ないことに対応します。 白色矮星内部は炭素でできていると仮定して\(A = 12\)とし、この式に観測されている白色矮星系列の暗い端の明るさ \(\log L/L_\odot \sim -4.5\)を代入すると、\(M = 0.6 M_\odot\)に対して\(\tau \sim 10^{10} \mathrm{yr}\)となります。 これは最も古い白色矮星の年齢をアタて、天の川銀河円盤の年齢の下限を与えるのに使うことができます。
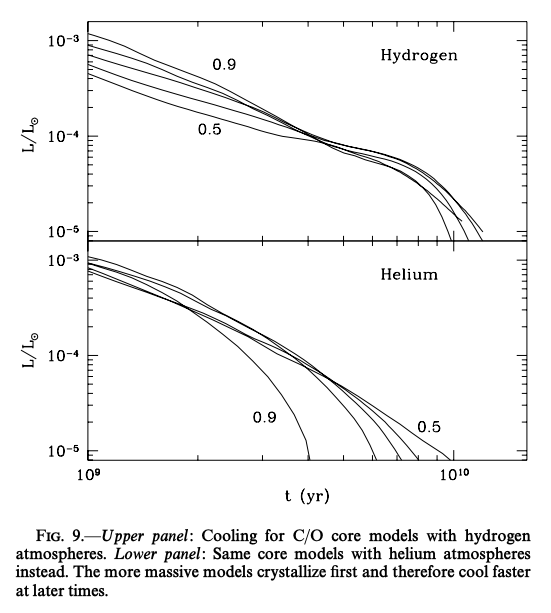
次の図は、精密なモデルから得られた光度と時間の関係を表したものです。
上パネルは最も外側に水素の層がある場合、下パネルは水素の層がないモデルを計算したものです。 水素の層の不透明度が大きいため、水素の層がある場合の方が冷却はゆっくり進行します。 比較的初期では、これまでの簡単なモデルから得られた \(\tau \propto L^{-5/7}\) の関係に良く一致していることがわかります。 後期になると結晶化のために冷却が速くなり、この関係から外れます。 初期は、質量の大きい白色矮星ほどイオン数が多いため、含まれる熱量が多く、冷えるまでに時間がかかります。 しかし結晶化が高い温度時点で起こるため、やがて小質量の白色矮星よりも速く冷却が進ようになります。
光度関数
白色矮星の光度関数 \(\Phi (L)\)は\(1\mathrm{pc}^3\)に1等級あたりに存在する白色矮星の数を表し、白色矮星の冷却率だけでなく、星形成の歴史についての情報を含んでいます。 太陽近傍の白色矮星に対して得られた光度関数は、\(\log L/ L_\odot \sim -4\)にピークを持ちます。 ピークの光度あたりからそれより暗い白色矮星に対しては、ボロメトリック補正の不確定さが大きな影響を及ぼし、エラーバーが大きくなります。
観測データから得られた光度関数から有用な情報を引き出すためには、それと比較すべき理論的な光度関数を作る必要があります。 ここでは、どのような原理で光度関数を得ることができるのかを概説します。
銀河円盤で星形成が始まった時刻を\(t=0\)とし、現在を\(t_\mathrm{g}\)とします。 ある恒星が\(t=t_\mathrm{b}\)に生まれ、現在は光度\(L\)の白色矮星になっている場合
という関係が成り立ちます。 ここで\(\tau_\mathrm{ev}\)は恒星が白色矮星になるまでにかかった時間、そして\(\tau_\mathrm{cool} (L)\)は白色矮星になってから光度が\(L\)になるまでにかかった時間、とします。 \(\tau_\mathrm{ev}\)は主系列星時代の質量\(M\)の関数であり、\(\tau_\mathrm{cool}\)は白色矮星の質量\(M_\mathrm{w}\)の関数です。 しかし\(M_\mathrm{w}\)と\(M\)との間には一対一の関係があると考えられるため、\(\tau_\mathrm{ev} + \tau_\mathrm{cool}\)は\(M\)の関数とみなすことができます。
\(\tau_\mathrm{ev} + \tau_\mathrm{cool}\)の上限は、\(t_\mathrm{g}\)で\(t_\mathrm{b}=0\)に対応します。 これは現在の光度\(L\)を持つ白色矮星の中で、主系列星時代の質量が最も小さかなったもの \(M = M_\mathrm{l} (L)\)になります。 一方、\(\tau_\mathrm{ev} + \tau_\mathrm{cool}\)の下限は、白色矮星になることのできる主系列星の最大質量 \(M = M_\mathrm{u} \sim 8M_\odot\)です。 我々の銀河円盤での星形成率を\(\psi (t)\)、初期質量関数を\(\phi (M)\)とすると、白色矮星の光度関数\(\Phi(L)\)は
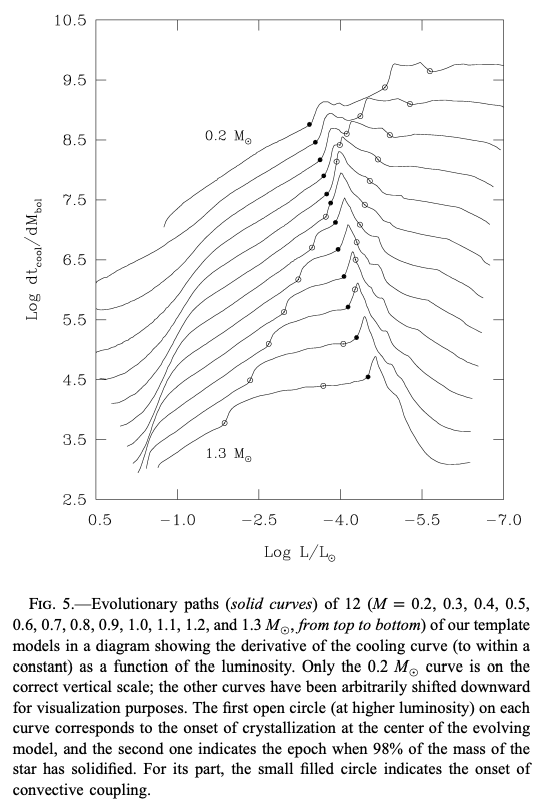
と表されます。 次の図は、\(\frac{d\tau_\mathrm{cool}}{dM_\mathrm{bol}}\)と光度の関係を示しています。
\(\frac{d\tau_\mathrm{cool}}{dM_\mathrm{bol}}\)の値が小さい方が冷却が速くなります (各質量に対する線は見やすさのために縦方向にずらされています。) 白色矮星が冷却されていき、温度が十分に下がる\((T_c \lesssim 6 \times 10^6 \mathrm{K})\)と、酸素炭素の結晶化が起こります。 各線上の最も左側に位置する丸で結晶化が起こり始め、その次の丸の位置では全体の98%の質量が結晶化された状態となります。 結晶化により潜熱が発生するため、冷却は一時的に遅くなります。 しかし、固体の比熱は液体よりも小さいため、結晶化したあとは冷却が速くなります。 結晶化は、密度が高い方が高温で起こるため、質量の大きな白色矮星ほど明るい時点で結晶化が起こります。 そして次の黒丸は、対流外層が発達し、その底と等温中心核の境界とが接するようになる部分を表します。 すると、対流によって熱が効率よく運ばれるため、冷却率が大きくなります。
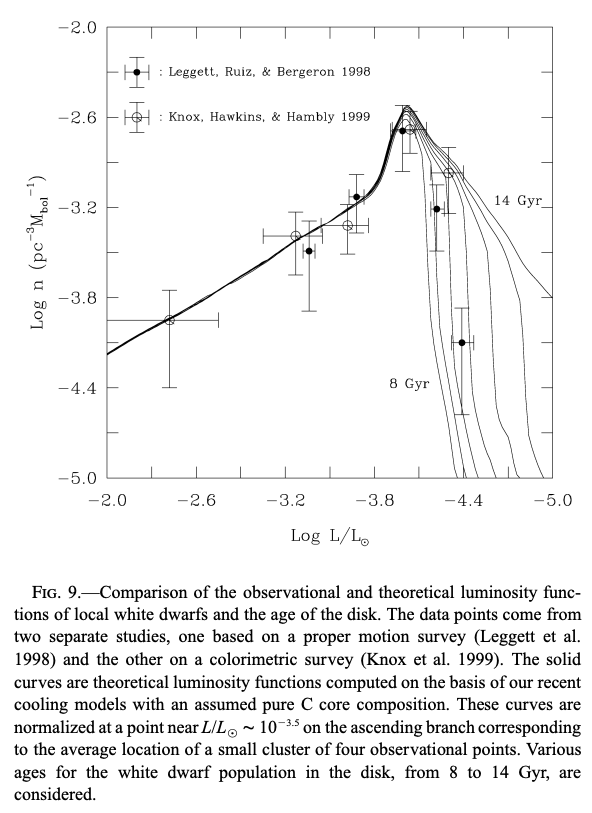
次の図は、理論的に得られた光度関数と、太陽近傍の白色矮星に対して得られたものとを比較したものです。
明るい側では理論関係と良い一致が得られ、暗い側の急激な数の減少が起こる光度から、最も古い白色矮星の年齢が100億年程度であるとわかります。 上の図の理論的な光度関数は、炭素中心核を持つ白色矮星モデルを使って得られたものです。 現実的な炭素・酸素中心核に対しては、年齢は10億年程度若くなることが予想されます。 これは、天の川銀河円盤で星形成が始まってから、現在までに経過した時間に対応します。
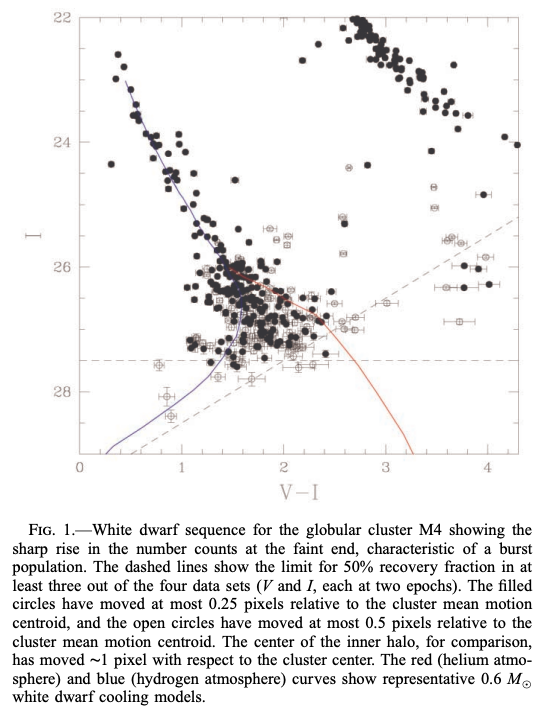
球状星団 M4 中の白色矮星
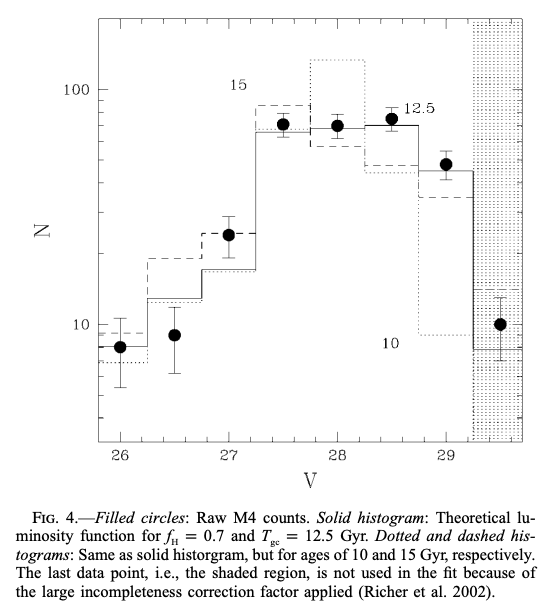
HSTによる球状星団 M4 (Vバンドのdistance modulus; 12.5)の長時間露出により、その中の白色矮星の光度関数のピークの暗さまで測光が可能になりました。 その光度関数のピークでの光度は、太陽近傍の白色矮星の光度関数のピークでの光度に比べて暗く、銀河円盤とハローには年齢の違いが有意にあることを示しています。 理論的な光度関数との比較により、球状星団 M4の年齢が\(12.7 \pm 0.7 \mathrm{Gyr}\)と求められました。 この年齢は、主系列の転向点光度をもとにして得られた年齢と合致しています。
参考文献
[1] Fontaine et al., 2001, “The Potential of White Dwarf Cosmochronology”
[2] Hansen, 1999, “Cooling Models for Old White Dwarfs”
[3] Hansen et al., 2002, “The White Dwarf Cooling Sequence of the Globular Cluster Messier 4”
[4] Shapiro & Teukolsky, “Black Holes, White Dwarfs, and Neutron Stars”