光度距離

ここでは宇宙論で大切な距離指標である光度距離(Luminosity distance)を導出しましょう。

絶対光度と見かけのフラックス

絶対光度の単位は\(L({\rm erg} \ s^{-1})\)、そして見かけのフラックスは\(f({\rm erg} \ s^{-1} {\rm cm}^{-2})\)より

\[L = 4\pi D_L^2 f\]

の関係にあります。よって光度距離を

\[D_L = \sqrt{\frac{L}{4\pi f}}\]

のように定義します。

光子数保存からの導出

光源が単一の振動数の光\(\nu\)を出しているとします。微小時間\(dt\)の間に出した光子の数

\[\frac{L}{h\nu} dt\]

は(伝搬の途中で吸収や消滅などを考えなければ)保存します。3次元的な距離を\(r\)として、さらに\(dt\)の時間間隔に光源から振動数\(\nu\)で出た光を、\(dt_0\)の時間間隔で振動数\(\nu_0\)で受け取るとすると

\[\frac{L}{h\nu} dt = \frac{4\pi r^2 f }{h \nu_0} dt_0\]

宇宙膨張の影響より、時間間隔が以下のように変化する。

\[\frac{dt}{a(t)} = \frac{dt_0}{a_0} \ \Longrightarrow \ dt_0 = (1+z) dt\]

さらに振動数も

\[\nu_0 = \frac{\nu}{1+z}\]

のように変化する。これらを代入すると

\[\frac{L}{4\pi f} = \frac{\nu}{\nu_0} \frac{dt_0}{dt} r^2 = (1+z)^2 r^2 \ \Longrightarrow \ \therefore \ D_L = (1+z) r(z)\]

となります。

例題: EdS宇宙

アインシュタイン・ド・ジッター宇宙のとき、すなわち\(K = 0, \Omega_{\rm DE, 0} = 0, \Omega_{r, 0} = 0, \Omega_{m, 0} = 1\)のとき

\[E(z) = (1+z)^{3/2}\]

より

\[\chi \underbrace{=}_{定義より} r = \frac{c}{H_0} \int_0^z \frac{dz}{(1+z)^{3/2}} = \frac{2c}{H_0} (1-\frac{1}{\sqrt{1+z}})\]

よって

\[D_L = \frac{2c}{H_0} (1+z - \sqrt{1+z})\]

となります。

例題: Totally flat model

\(\Omega_{r, 0} = 0, \Omega_{m, 0} + \Omega_{\rm DE, 0} = 1, \Omega_{m, 0} + \Omega_{\Lambda, 0} = 1\)のとき、\(\Omega_{\Lambda, 0} = 1-\Omega_{m, 0}\)より

\[D_L = \frac{c}{H_0} (1+z)\int_0^z \frac{dz}{(\Omega_{m, 0} (1+z)^3 + 1-\Omega_{m, 0})^{1/2}}\]

となります。\(\Omega_{m, 0} = 0\)で\(D_L = \frac{c}{H_0} (1+z) z\)となります。

以下にこのモデルでの光度距離を計算するPythonスクリプトとその計算例を掲載します。

#!/usr/bin/env python3 

from scipy import integrate
import numpy as np
import matplotlib.pyplot as plt

# define integrand
def func(omega_m, z):
    return 1 / np.sqrt(omega_m*(1+z)**3+1-omega_m)

if __name__ == '__main__':
    # set variables
    iz = 100
    # set plot range
    zmin = 0.0
    zmax = 5.0
    # set density parameter
    oms = (0.0, 0.3, 1.0)
    # set z coordinate
    zlist = np.linspace(zmin, zmax, iz)
    # set Romberg integrate step
    izz = 1 + 2 ** 6
    # main loop
    for om in oms:
        # set empty list for dl
        dl = []
        # compute [0:z] integration
        for z in zlist:
            zz = np.linspace(0.0, z, izz)
            # compute luminosity distance
            d = (1+z) * integrate.romb(func(om, zz), dx=zz[1]-zz[0])
            dl.append(d)
        # make plot
        plt.plot(zlist, dl)
    # show plot
    plt.show()

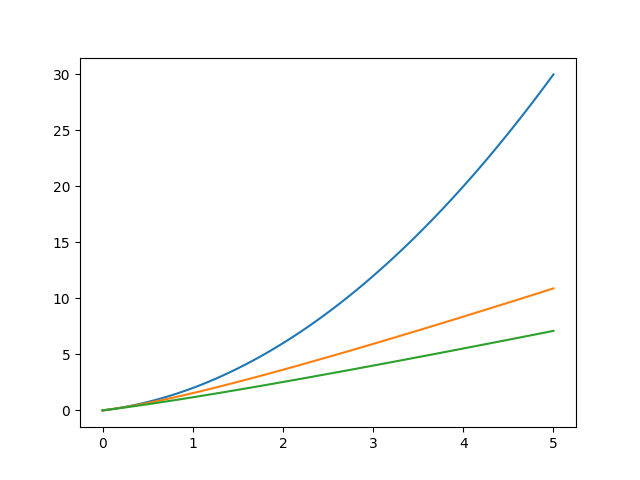
光度距離の作図例

青, オレンジ, 緑線の順に、\(\Omega_{m, 0} = 0, 0.3, 1.0\)のプロット。横軸: 赤方偏移、縦軸: \(D_L/(c/H_0)\)

距離指数 (Distance modulus)

ある天体を観測したときの見かけの等級を\(m\)、その天体の絶対等級を\(M\)とすると

\[m - M = 5 \log_{10} \frac{D_L}{10{\rm pc}}\]

近年では宇宙論で用いられる距離指標として、Ia型超新星があります。