不透明度 (opacity)

吸収係数のロスランド平均は、ガスの密度・温度・元素組成の関数として与えられます。これを単にガスの不透明度(opacity)と呼ばれることが多いです。 (5.1.16)式は、温度勾配と輻射による(局所的な)光度 \(L_{r, \mathrm{rad}}\)との関係を与えます。この関係から、不透明度が大きいほど、大きな温度勾配が必要であることを示しています。このように、ガスの不透明度の値は、恒星の内部構造(物理量の分布)にとって重要な量となります。
不透明度に寄与するプロセスには、bound-bound吸収 (線吸収)・bound-free吸収・free-free吸収、そして電子散乱(electron scattering)などがあります。

電子散乱

電子散乱による不透明度 \(\kappa_\mathrm{el}\)は、トムソン散乱断面積\(\sigma_T = 6.65 \times 10^{-25} \mathrm{cm^2}\)に、1グラムあたりの電子数を乗じたものになります。 1グラムあたりの電子数は\(\frac{1}{\mu_e m_p} (=\frac{N_A}{\mu_e})\)で表されます。そして電子の平均分子量\(\mu_e\)は、完全電離したガスでは\(\mu_e = \frac{2}{1+X}\) (\(X\)は水素の質量含有量)と書けます。したがって、完全電離したガスでは\(\kappa_\mathrm{el}\)は、温度と密度に対する依存性を持たず

\[\kappa_\mathrm{el} = \frac{\sigma_T}{\mu_e m_p} = \sigma_T \frac{N_A}{2} (1+X) \simeq 0.20 (1+X) \ [\mathrm{cm^2 / g}] \tag{5.2.1}\]

のように表されます。ただし、非常に高音(\(T \gg 10^8 \mathrm{K}\))では、コンプトン効果に伴って電子散乱の不透明度は、上式の値よりも小さくなります。電子散乱による不透明度は不透明度の下限となっており、密度が小さく高温の領域で重要になります。そのような場所ではbound-bound・bound-free・free-freeによる不透明度が小さくなり(後述)、電子散乱不透明度が卓越するためです。

Free-free吸収

Free-free吸収は制動放射の逆過程であり、自由電子がイオンの電場で散乱される際に、光を吸収する過程で起こります。 (自由電子と光子だけでは、エネルギー保存と運動量保存を同時に満たすことができないため、第三者のイオンが必要となります。)
最初に制動放射の発光係数を与え、キルヒホッフの法則を用いて、free-free吸収の吸収係数を求めてみましょう。
(ただし、ここでは詳細な式変形は省略します。詳しくは熱制動放射と熱制動吸収のページをご覧ください。)
加速度運動する1つの電子(電荷\(e\))が、単位時間あたりに放出する電磁波のエネルギーは、ラーモアの式より\(\frac{2e^2}{3c^3} \dot{v}^2\)で与えられます。ここで電子の運動は非相対論的であるとしました。ここで\(\dot{v}\)は電子の加速度を表します。電荷\(Z_i e\)を持つイオンのそばを通過する場合の加速度は\(\dot{v} = \frac{Z_i e^2}{m_e r^2}\)のように書けます。ここに\(r\)は電子とイオンの距離を表します。電子の速度が(非相対論的ではありますが)十分高速で、電子は次の図のようにほぼ直線的に通過すると近似すると、衝突パラメータ\(b\)で通過する電子が放出する全放射エネルギーは

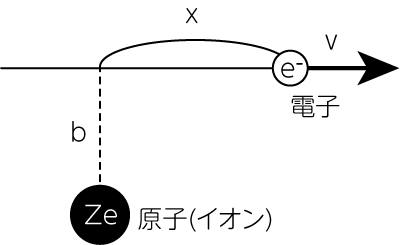
\[E_b = \frac{2e^2}{3c^3} \frac{Z_i^2 e^4}{m_e^2} \int_0^\infty \frac{dt}{(b^2 + x^2)^2} = \frac{2e^6 Z_i^2}{3 m_e^2 c^3} \frac{1}{v} \int_{-\infty}^\infty \frac{dx}{(b^2 + x^2)^2} = \frac{\pi e^6 Z_i^2}{3 m_e^2 c^3} \frac{1}{vb^3} \tag{5.2.3}\]

のように求めることができます。この過程では、電子は\(x \sim 0\)のあたりで最も電磁波を強く発します。その強さは\((b^2 + x^2)^{-2}\)に比例します。よって、\(x = vt\)として\(\vert vt \vert \ll b\)の範囲で展開を行うと

\[E(t) \propto \frac{1}{(b^2 + v^2 t^2)^2} \approx \frac{1}{b^4} \left( 1 - \frac{2v^2 t^2}{b^2}\right) \tag{5.2.4}\]

と書けます。一方、これを\(\cos (\omega t)\)に比例する電磁波によるエネルギー(\(\propto \cos^2 (\omega t)\))と考えると、\(\omega t \ll 1\)で

\[E(t) \propto \cos^2 (\omega t) \approx 1 - \omega^2 t^2 \tag{5.2.5}\]

のようになります。これと(5.2.4)式を比較すると

\[\omega \simeq \frac{\sqrt{2} v}{b} \simeq \frac{v}{b} \tag{5.2.6}\]

という関係を得ます。これはある電子の速度に対して、衝突パラメータ\(b\)は近似的に電磁波の振動数に関係づけられることを表しています。イオンと電子間の相対速度\(v\)が与えられているとき、様々な衝突パラメータ\(b\)での遭遇によって放出される電磁波の角振動数が\(\omega \sim \omega + d\omega\)である衝突の衝突パラメータの面積は\(-2\pi b db\) (\(b\)が小さいほど、\(\omega\)が大きいので負の符号がつきます)なので、1つの衝突で放出される単位振動数あたりのエネルギー\(E_\omega\)は

\[E_\omega d\omega = -2\pi b E_b db = - \frac{2\pi^2 e^6 Z_i^2}{3 m_e^2 c^3} \frac{1}{vb} db \simeq \frac{2\pi^2}{3} \frac{e^6 Z_i^2}{m_e^2 c^3 v^2} d\omega \tag{5.2.7}\]

と表されます。電子およびイオンの数密度を\(N_e, N_i\)と書くと、単位時間・単位体積・単位振動数あたりに放出されるエネルギー\(4\pi \rho \eta_\omega^{ff}\)は

\[4\pi \rho \eta_\omega^{ff} = N_i N_e \int_{v_\mathrm{min}}^\infty E_\omega v f(v) dv \tag{5.2.8}\]

と表されます。ここで\(f(v)\)は、相対速度が\(v \sim v + dv\)にある確率を与える分布関数です。熱運動の場合は、規格化されたマクスウェル・ボルツマン分布

\[f(v) dv = 4\pi \left( \frac{m_e}{2\pi k_B T}\right)^{3/2} \exp \left( - \frac{m_e v^2}{2k_B T}\right) v^2 dv \tag{5.2.9}\]

で与えられます。 (5.2.8)式の積分の下限値\(v_\mathrm{min}\)は、電子の運動エネルギーが放出される光子のエネルギーよりも大きくなければならないという条件から

\[\frac{1}{2} m_e v_\mathrm{min}^2 = \hbar \omega \tag{5.2.10}\]

のように設定できます。 (5.2.9), (5.2.10)式を用いて、(5.2.8)式の積分を実行すると

\[4\pi \rho \eta_\nu^{ff} \simeq \frac{2\pi e^6 Z_i^2}{3 m_e c^3} \left( \frac{2\pi}{m_e k_B T}\right)^{1/2} N_e N_i e^{-\frac{h\nu}{k_B T}} \tag{5.2.11}\]

が得られます。これにキルヒホッフの法則を用いれば

\[\rho \kappa_\nu^{ff} \simeq N_e N_i \frac{e^6 Z_i^2}{12 m_e c h} \left( \frac{2\pi}{m_e k_B T}\right)^{1/2} \nu^{-3} \left( 1 - e^{-\frac{h\nu}{k_B T}}\right) \tag{5.2.12}\]

となります。ロスランド平均不透明度をとると

\[\kappa^{ff} \propto \frac{Z_i^2 N_e N_i}{\rho} T^{-7/2} \propto \rho T^{-3.5} \tag{5.2.13}\]

を得ます。ここから、単位質量あたりのロスランド平均不透明度は密度に比例して大きくなり、温度が高いと急激に小さくなるとわかります。 \(T^{-3.5}\)の依存性は、\(\kappa_\nu^{ff}\)が\(T^{-1/2} \nu^{-3}\)に比例することから、ロスランド平均不透明度を得る際の積分で\(\nu^{-3} \propto \left(\frac{h\nu}{k_B T})^{-3]\)となることから現れるものです。係数を計算すると、free-free吸収におけるロスランド平均不透明度は、cgs単位で近似的に

\[\kappa^{ff} \approx 10^{23} \frac{\langle Z_i^2\rangle}{\mu_e \mu_I} \rho T^{-3.5} \ [\mathrm{cm^2 / g}] \tag{5.2.14}\]

のように表されます。ここで\(\mu_e, \mu_I\)はそれぞれ電子とイオンの平均分子量を表します。

Bound-free吸収

Bound-free吸収は、原子またはイオンに束縛されていた電子が光を吸収することで、束縛から離れて自由電子になる(電離する)過程で起こります。束縛電子に対する電離エネルギー以上のエネルギーを持つ光子しか吸収しないため、bound-freeの吸収係数の波長に対する形はノコギリの歯状となります。 (Bound-free吸収は、古典的には電子がfree-free放射をした後に再結合する過程の逆過程と考えることができます。)

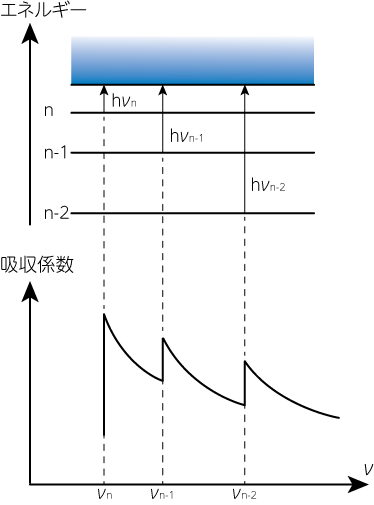
不連続と不連続の間での吸収係数は、free-free吸収のロスランド平均不透明度と同じように考えることができるため、\(\rho T^{-3.5}\)に比例します。水素・ヘリウムがほぼ完全に電離しているガスでは、bound-free吸収のロスランド平均不透明度\(\kappa^{bf}\)は、近似的に

\[\kappa^{bf} \approx 4 \times 10^{25} Z (1 + X) \rho T^{-3.5} \ [\mathrm{cm^2 / g}] \tag{5.2.15}\]

のよう表されます。水素・ヘリウムが不完全電離の場合には、電子数密度\(N_e\)が温度によって急激に変化するため、\(\kappa^{bf}\)の温度依存性は\(T^{-3.5}\)からかけ離れているので注意が必要です。例えば太陽のような低温度星の表面近くでは、負の水素イオン\(\mathrm{H}^-\)のbound-free吸収が重要です。 \(3000 \leq T \leq 6000 \mathrm{K}\)では、水素はほとんど電離しておらず、電子はNa, K, Ca, Alなどの金属から供給されます。ここでも電子数密度\(N_e\)は温度によって急激に変化するため、\(\mathrm{H}^-\)のbound-free吸収のロスランド平均不透明度は、大体T^{10}に比例することが知られています。
次の図は、有効温度が5040度の低温度星と、28300度の高温度星の光球でのbound-freeとfree-free吸収の吸収係数を、波長の関数として表したものです。低温度星の表面近くでは、負の水素イオンのbound-free吸収が可視光領域で重要です。また表面温度が数万度の早期型星の表面では、水素とヘリウムのbound-free吸収が重要となります。

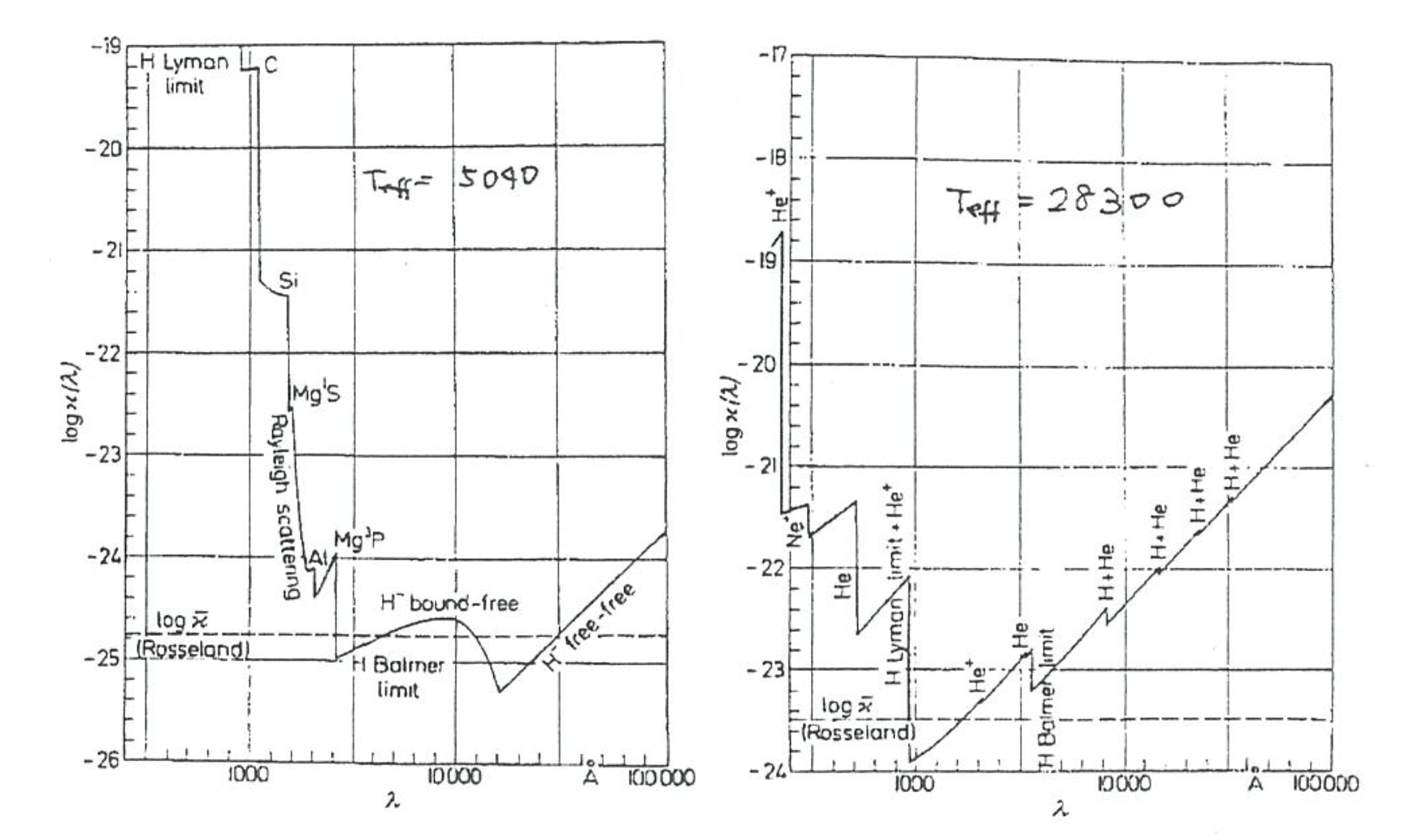
Bound-bound吸収

Bound-bound吸収は、原子またはイオンに束縛された電子のエネルギー状態の遷移に伴う吸収です。離散的なエネルギーで起こるため、線吸収とも呼ばれます。非常にたくさんの遷移が可能であるため、\(\kappa_\nu - \nu\)図では、free-freeとbound-free吸収に起因する連続吸収の上に、無数のbound-bound吸収によるピークが林立します。

不透明度のテーブル (opacity tables)

このように非常にたくさんの種類の吸収を恒星内部で実現されている温度と密度に対してもれなく評価し、ロスランド平均不透明度を得るには、非常に大きな労力を割く必要があります。現在では世界でわずかなグループだけが、恒星内部の温度と密度に対する不透明度テーブルを出しています。最近では、ロスアラモス研究所のグループが出したOPLIB tablesと呼ばれるものが公開されたようです。不透明度の温度と密度に対する依存性の一例を、下図に示します。下図はOPLIB tablesの1つで、\(X = 0.70, Z = 0.02\)の標準的な元素組成に対するものです。

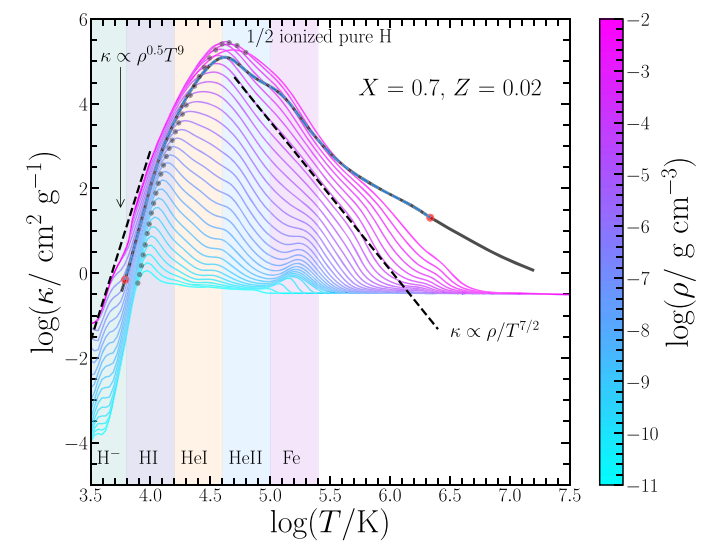
上図の温度が高いほど不透明度が減少しているのは、free-freeおよびbound-free不透明度が、近似的に\(\rho T^{-3.5}\)に比例することを表しています。また密度が大きいほど不透明度が大きいことも図に表れています。さらに高温低密度で不透明度が一定になっていますが、これは電子散乱による不透明度によるものです。低温度側で、温度の上昇に伴って不透明度が急激に大きくなっている部分では、負の水素イオンによる吸収が重要となっています。また不透明度は密度が大きいほど大きな値を持ち、水素含有量や重元素含有量が多いほど大きくなります。
この図からわかるように、不透明度は温度が数万度のところに2つのピークを持ちます。これらは水素の電離と、ヘリウムの一回・二回電離領域に対応します。また\(T \sim 2 \times 10^5\)Kにあるピークは、主に鉄の内閣電子のエネルギー遷移によって作られます。そのピークは恒星の振動の励起に重要な影響を及ぼしますが、その存在は1990年代に入って初めて認識されるようになりました。この発見により、以前には説明ができなかった脈動変光星の様々な性質が明らかになりました。

参考文献

[1] Colgan et al., 2016, “A New Generation of Los Alamos Opacity Tables”
[2] An Expanded Set of Los Alamos OPLIB Tables in MESA: Type-1 Rosseland-mean Opacities and Solar Models
[3] The Opacity Project
[4] Fortran Subroutines for OPAL Stellar Opacities
[5] 高原文郎, “宇宙物理学”
[6] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”