Table of contents
円形加速器
ここでは荷電粒子を高エネルギーまで加速する円形装置についてご紹介します。
サイクロトロン加速器
荷電粒子が一様磁場中で円運動することを利用して作られた粒子加速器です。D電極と呼ばれる電極中に一様磁場を用意します。それを2つ並べ、その電極に交流電圧をかけることで、D電極間に電位差を生じさせます。 D電極内を半周して出てきた荷電粒子をその電位差による電場で加速を行います。
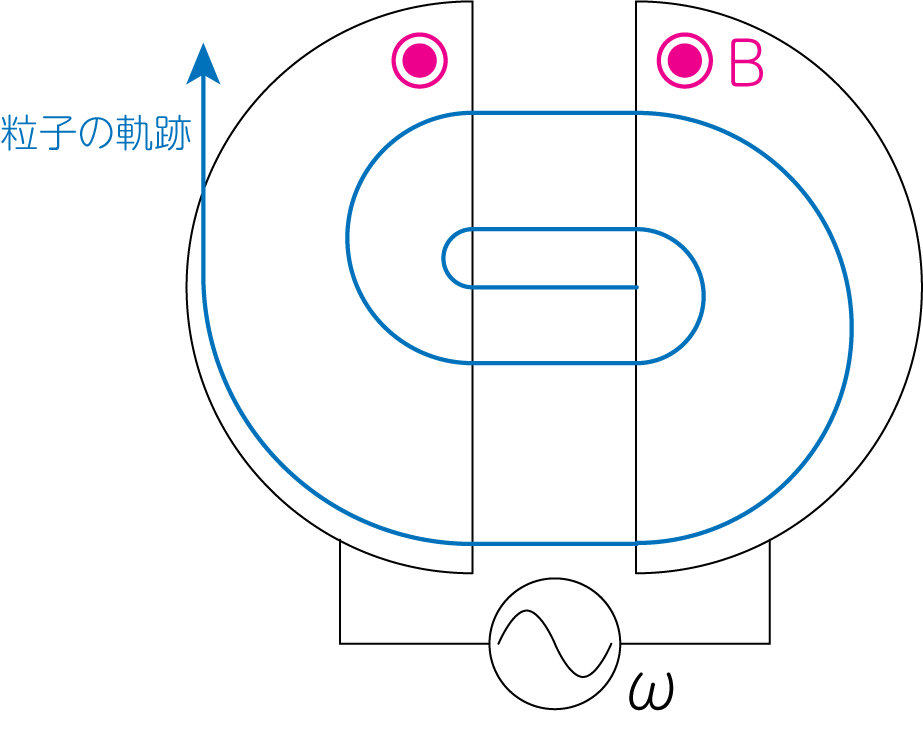
荷電粒子の電荷を\(q\)とすると、\(z\)方向の一様磁場\(B\)中における荷電粒子の運動方程式は
\[m \dot{\mathbf{v}} = q \mathbf{v} \times \frac{\mathbf{B}}{c} \ \Longrightarrow \ \left\{ \begin{array}{c} m \frac{dv_x}{dt} = q v_y \frac{B}{c} \\ m \frac{dv_y}{dt} = - q v_x \frac{B}{c} \end{array}\right. \tag{1}\]のように書かれます。\(Z \equiv v_x + i v_y\)とおくと、この連立微分方程式を簡単に解くことができます。
\[m \frac{dZ}{dt} = iq \frac{B}{c} Z \ \Longrightarrow \ Z = Z_0 e^{i\frac{qB}{mc} t} \tag{2}\]ここで\(\omega_\mathrm{ce} \equiv \frac{qB}{mc}\)はサイクロトロン振動数です。振動周期\(T\)は
\[T = \frac{2\pi}{\omega_\mathrm{ce}} = \frac{2\pi m c}{qB} \tag{3}\]となります。(3)式は粒子の速度に依存せず、\(B = (一定)\)ならば\(T=(一定)\)という等時性と呼ばれる性質があります。よって交流\(V(t) = V_0 \cos \omega_\mathrm{ce} t\)で加速することで、半周期\(T/2\)毎に電場\(V_0 / d\)により加速されます。 この装置により、荷電粒子は一回の加速で\(q V_0\)のエネルギーを受け取ることができ、\(n\)周期後には\(2n q V_0\)のエネルギー上昇が見込めます。
しかし、問題はそう簡単ではありません。荷電粒子の速度が光速度\(c\)に近づくと、相対論的な効果により質量が\(m\gamma\)となります。そのため、周期\(T\)の等時性が破れます。これにより加速効率が悪くなり、最終的には加速されない0点に到達します。
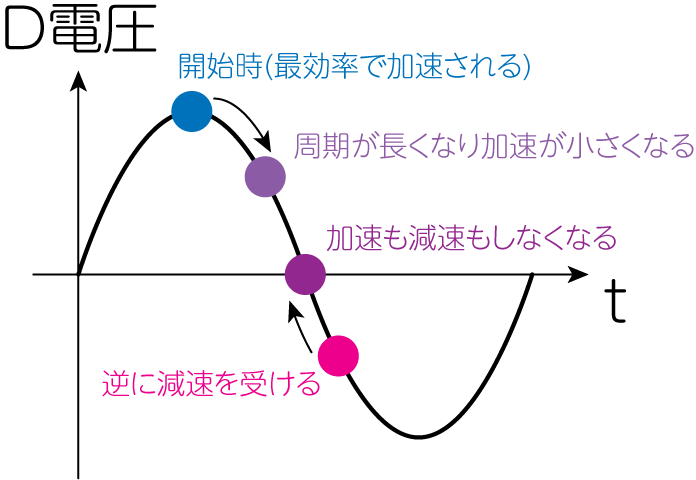
マイクロトロン加速器
サイクロトロン運動を利用したもう加速器は他にも存在します。一様磁場中を円運動する荷電粒子を、ある領域を通過する毎に加速していくというシンプルなものです。
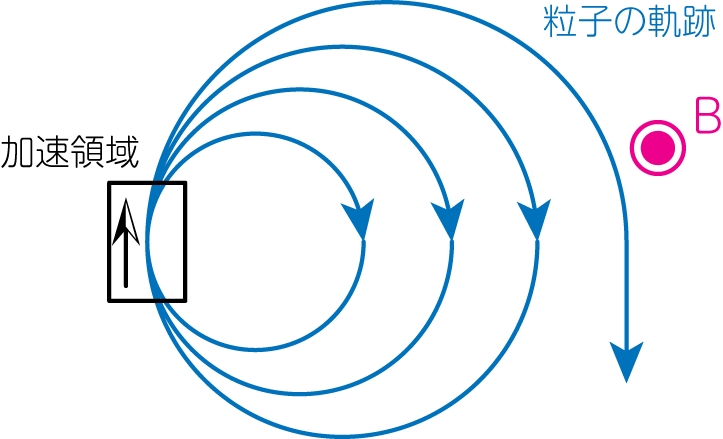
\(\omega_\mathrm{ce} = \frac{qB}{mc}\)、周期\(T = \frac{2\pi mc}{qB}\)は先程のサイクロトロン加速器と同じです。1ターン(1回の加速)で得ることができるエネルギーを\(\Delta E = \Delta m c^2\)とすると、周期は
\[\Delta T = \frac{2\pi \Delta m c}{qB} \tag{4}\]のように徐々に大きくなっていきます。\(\Delta T\)が加速領域の加速周期\(T_\mathrm{rf}\)の整数倍であれば、荷電粒子を順調に加速させることができます。よって
\[\frac{2\pi \Delta m c}{qB} = n T_\mathrm{rf} \tag{5}\]1回目の加速までに加速領域の交流電場周期が\(\ell\)回振動をしていたとすると
\[\frac{2\pi (m+\Delta m) c}{qB} = \ell T_\mathrm{rf} \tag{6}\](6)式から(5)式を引き算すると
\[\frac{2\pi mc}{qB} = (\ell -n) T_\mathrm{rf} \tag{7}\]\(\ell -n\)が最小のとき、すなわち\(\ell-n=1\)のとき、磁場\(B\)の値は最大となります。すなわち、これは軌道半径が最も小さいときを意味します。この\(\ell-n=1\)の場合を考えると
\[\frac{(6)}{(5)} = \frac{m+\Delta m}{\Delta m} = \frac{\ell}{n} \ \Longrightarrow \ m = \left( \frac{\ell}{n} -1 \right) \Delta m = \frac{\Delta m}{n} \tag{8}\]よって\(n=1\)のとき、(8)式から、一度の加速で\(\Delta m = m\)だけエネルギーを与えることができることができます。また(5)式から加速周期も一番小さく、コストも小さく済みます。
ただし、この加速器は加速するごとに加速効率が悪くなる上に、荷電粒子の軌道も加速とともに大きくなっていきます。よって長い間、加速し続けることは難しく、(装置の規模にもよりますが)せいぜい10-30ターン程度の加速とされています。 また装置全体を小さくするためには、加速領域も小さくしなければなりません。よってマイクロトロン加速器は電子や陽電子などの加速に特化したものとされています。
ベータトロン加速器
マクスウェル方程式の一つである、ファラデーの法則を用いて粒子を加速する装置です。運動方程式は(ローレンツ力)=(遠心力)の釣り合いが維持され、半径\(R_0\)で一定の円周上を円運動しているものとします。 また磁場は\(z\)方向にしか存在しないものとします。
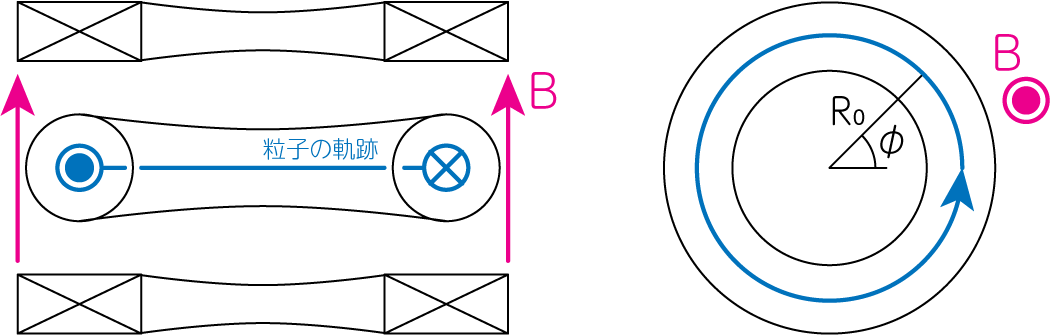
以下では電子の運動を考えましょう。動径方向の釣り合いの式より
\[-e \left( \mathbf{v} \times \frac{\mathbf{B}}{c} \right)_R + \frac{m v_\varphi^2}{R_0} = 0 \ \Longrightarrow \ v_\varphi = \frac{e R_0}{m_e c} B \tag{9}\]ファラデーの法則を半径\(R_0\)の円盤で面積分します。するとストークスの定理より
\[\begin{align} &\iint_{\pi R_0^2} \nabla \times \mathbf{E} \cdot d\mathbf{S} = \oint_{R=R_0} \mathbf{E} \cdot d\mathbf{s} \underbrace{=}_{系の軸対称性より} 2\pi R_0 E_\varphi = - \frac{1}{c} \iint_{\pi R_0^2} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = -\frac{1}{c} \frac{\partial \Phi}{\partial t} \notag \\ &\Longrightarrow \ E_\varphi = -\frac{1}{2\pi c R_0} \frac{\partial \Phi}{\partial t} \tag{10} \end{align}\]を得ます。ここで\(\Phi\)は半径\(R_0\)の円板上の磁束です。磁束の時間変化が\(\varphi\)方向の誘導電場を生み出すという式です。すると\(\varphi\)方向の運動方程式より
\[m_e \frac{dv_\varphi}{dt} = -e E_\varphi \ \Longrightarrow \ \frac{e R_0}{c} \frac{dB}{dt} = \frac{e}{2\pi cR_0} \frac{\partial \Phi}{\partial t} \ \Longrightarrow \ B = \frac{1}{2} \frac{\Phi}{\pi R_0^2} \tag{11}\](11)式の右辺に現れた\(\Phi/ (\pi R_0^2)\)は、半径\(R_0\)の円板内での平均磁場を意味します。平均磁場の半分の磁場を\(R_0\)の円周上に配置できれば、 電子は円運動をしながら\(E_\varphi\)により加速されることがわかります。
シンクロトロン加速器
質量\(m\)、電荷\(q\)の荷電粒子を下図のような円形加速器で加速することを考えます。
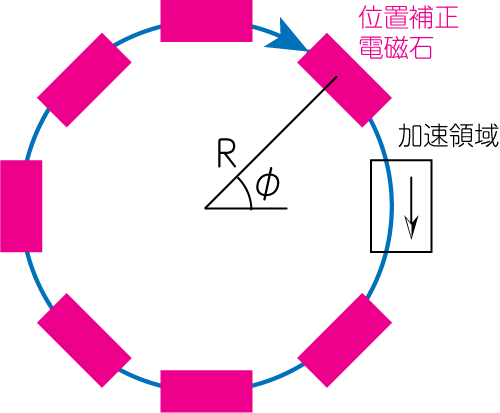
荷電粒子の軌道を円形に保つために、位置補正部分ではこの紙面に垂直な磁場\(\mathbf{B} = B \mathbf{e}_z\)を加えます。荷電粒子の運動はこの紙面内に限られているとし、\(\mathbf{v} = v_R \mathbf{e}_R + \mathbf{v}_\varphi \mathbf{e}_\varphi\)のように書きます。また荷電粒子はすでに相対論的速度に達しているとすると、相対論的運動方程式から
\[\frac{d}{dt} (m\gamma \mathbf{v}) = q\mathbf{v} \times \frac{\mathbf{B}}{c} \ \Longrightarrow \ \left\{ \begin{array}{l} \frac{d}{dt} (mc\gamma \beta_R) = q \beta_\varphi B \\ \frac{d}{dt} (mc \gamma \beta_\varphi) = -q \beta_R B \end{array}\right. \tag{12}\]サイクロトロン加速器のときと同様に\(Z \equiv \beta_R + i \beta_\varphi\)と置換すると
\[\frac{d}{dt} (mc \gamma Z) = iq B Z \tag{13}\]さらに粒子の速度はすでに超相対論的なものに到達し、加速も減速もされないような定常状態に落ち着いているものとします。すなわち\(m \gamma \sim (一定)\)と仮定すると
\[\frac{dZ}{dt} = i\frac{q B}{m c \gamma} Z \ \Longrightarrow \ Z = Z_0 e^{i\frac{qB}{mc\gamma} t} = Z_0 e^{i\omega_\mathrm{se} t} \tag{14}\]ここで\(\omega_\mathrm{se} = \frac{qB}{mc\gamma}\)はシンクロトロン振動数です。軌道半径\(R_0\)と軌道を周回する速度\(v_\varphi\)の関係式より
\[R = \frac{v_\varphi}{\omega_\mathrm{se}} \underbrace{=}_{\beta_\varphi = c \beta_\varphi} \ \Longrightarrow \ q B = \frac{mc^2 \gamma \beta_\varphi}{R} \tag{15}\]ここで(12)式の\(R\)成分より
\[m c \gamma \dot{\beta}_R = \frac{mc^2 \gamma \beta_\varphi^2}{R} \ \Longrightarrow \ \dot{\beta}_R = \frac{c \beta_\varphi^2}{R} \tag{16}\]となります。運動する点電荷が放出する輻射場のエネルギーはリエナーの公式で与えられるのでした。磁場が与えるローレンツ力は常に粒子の速度に直交することから、\(\dot{\mathbf{v}} = \dot{v}_R \mathbf{e}_R\)と\(\boldsymbol{\beta}\)は垂直であるとしてこれを計算してみると
\[P = \frac{2q^2}{3c^3} \{ \gamma^6 (\dot{v}^2 - \vert \dot{\mathbf{v}} \times \boldsymbol{\beta} \vert^2)\} = \frac{2q^2}{3c^3} \gamma^6 \underbrace{\dot{v}^2}_{(16)} (1-\beta^2) = \frac{2q^2}{3c^3} \gamma^4 \frac{c^4 \beta_\varphi^4}{R^2} \propto \frac{E^4}{R^2} \tag{17}\]のようになります。粒子の運動が超相対論的であることから、\(E = \sqrt{p^2 c^2 + m^2 c^4} \simeq p c = m c^2 \gamma \beta\)と書けることを利用しました。 (17)式から、軌道半径\(R\)が大きいほど、輻射によるエネルギー損失は小さくなります。2012年にヒッグス粒子を発見したCERNの円形加速器LHCは27kmの円周長を持ちます。 このように実験装置を巨大にすることで、今日の高エネルギー実験が可能になったのです。
日本の山手線の一周は34.5kmで、これより少し大きいくらいです。