Table of contents

1. Time to solution (TTS)
   1. 概念
   2. 計算方法
   3. 実際のTTSの描画
2. 参考資料

Time to solution (TTS)

概念

アニーリングアルゴリズムはどのような計算時間でも何かしらの近似解を算出することができます。しかしいくら計算が速くても、誤った解が求まるようでは意味がありません。そこで自分が必要な確率で最適解が算出されるまでの計算時間を求め、それをアニーリングアルゴリズムの良し悪しを考える指標に用いましょう。

アニーリングアルゴリズムは複数回行い、その中から最適解を探します。そのため、計算時間を評価するには複数回の実行も考慮に入れる必要があります。

これらを踏まえた上で、ある確率で最適解を求めるまでにかかる計算時間をTime to solution (TTS)と呼びます。

計算方法

1回のアニーリング時間を\(\tau\)とし、そのアニーリングで最適解が求まる確率(成功確率)を\(p_s (\tau)\)とします。よって1回のアニーリングで最適解が求まらない確率は\(1-p_s(\tau)\)となります。これを\(R\)回繰り返すとき、この\(R\)回全てで最適解が求まらない確率は\((1-p_s (\tau))^R\)と計算されます。よって\(R\)回のうち、1回でも最適解を得る確率\(p_R\)は

\[p_R = 1- (1-p_s (\tau))^R\]

この式を\(R\)について整理すると

\[R = \frac{\ln (1-p_R)}{\ln (1-p_s (\tau))}\]

となります。これに1回のアニーリングにかかる時間\(\tau\)を掛ければ、\(R\)回のアニーリングにかかる総計算時間です。

\[\mathrm{TTS} (\tau, p_R) = \tau \frac{\ln (1-p_R)}{\ln (1-p_s (\tau))} \tag{1}\]

\(\mathrm{TTS} (\tau, p_R)\)は、1回のアニーリング時間\(\tau\)、最適解が求まる確率\(p_s (\tau)\)のアルゴリズムを用いて最適解が得られるとき、確率\(p_R\)で最適解が得られるまでの繰り返し回数も考慮した計算時間です。

実際のアルゴリズム評価では、\(p_R\)は定数として与えます。研究などで用いられる値としては、\(p_R=0.99\)が多いようです。様々なアニーリング時間\(\tau\)のアニーリングを複数回実行することで\(p_s (\tau)\)を計算し、それらを用いて\(\mathrm{TTS} (\tau, p_R)\)を計算します。

実際のTTSの描画

下図は最適解がわかっているナップサック問題についてのTTSを描画したものです。横軸にアニーリング時間、縦軸に(1)式のTTSを対数スケールで描画しています。

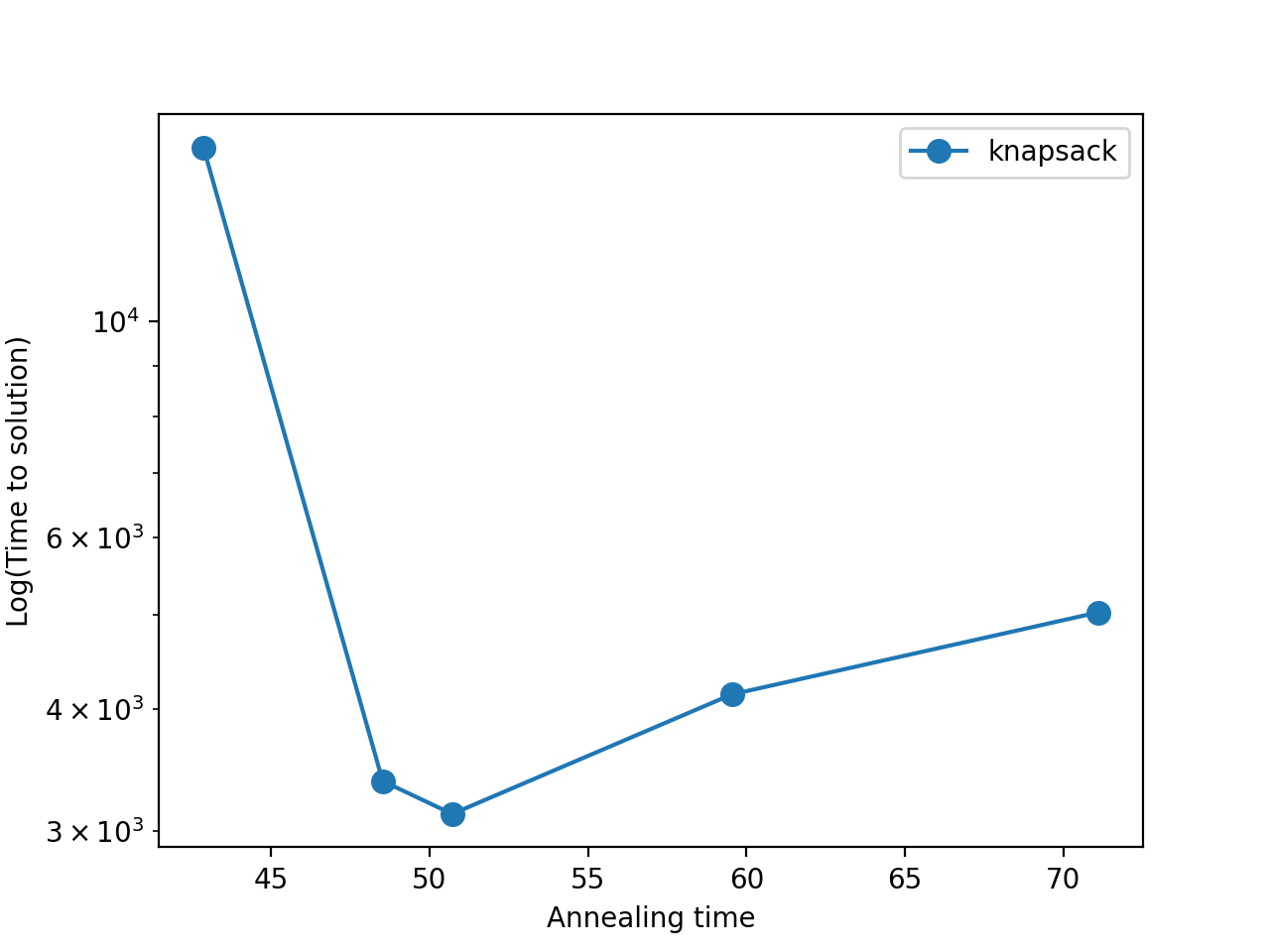
アニーリング時間を大きくしていくと最適解に到達する確率が上がるため、TTSは小さくなります。しかしアニーリング時間をある値以上にすると、今度は(1)式が\(\tau\)に比例していることから、TTSも大きくなっていきます。一般にTTSは下に凸になるような概形となります。

参考資料

• 西森秀稔, 大関真之, 量子アニーリングの基礎
• OpenJijチュートリアル, 2-アニーリングアルゴリズムの評価

※ 2つ目の資料は私が執筆したもので、ほぼ同じ内容です。