Table of contents
統計力学の復習
カノニカル分布
カノニカル分布の分布関数は以下のように書けるのでした。
\[P ({\bf x}) = \frac{1}{Z} e^{-\beta E({\bf x})} \tag{1.1}\] \[Z = \sum_{\bf{x}} e^{-\beta E({\bf x})} \tag{1.2}\]ここで\(\beta = 1/ T\)は逆温度、\(E({\bf x})\)は状態のエネルギーです。
例として、\(x = \pm 1\)のような2値しか取らない場合を考えましょう。これを電子や原子のスピンの上向き・下向きだとします。ここに外磁場\(h\)を印加させると、系のエネルギーは
\[E (x) = -hx \tag{1.3}\]のようになります。これを(1.1), (1.2)式に代入すると
\[P(x) = \frac{1}{Z} e^{\beta h x} \tag{1.4}\] \[Z = \sum_x e^{\beta h x} = e^{\beta h} + e^{-\beta h} = 2 \cosh (\beta h) \tag{1.5}\]が得られます。統計力学においては分布が重要です。しかし、それをそのまま扱うのは困難なので、その分布から得られる期待値などを計算します。
\[\langle x \rangle = \sum_x x P (x) = \frac{1}{Z} (e^{\beta h} - e^{-\beta h}) = \frac{2 \sinh (\beta h)}{2 \cosh (\beta h)} = \tanh (\beta h) \tag{1.6}\]となります。
ヘルムホルツの自由エネルギー
ここで自由エネルギーを導入しましょう。
\[-\beta F = \log Z \tag{1.7}\]すると
\[\beta \langle x \rangle = \frac{\partial}{\partial h} \log Z \tag{1.8}\]のようになっていることがわかります。もし自由エネルギーを計算できれば、分配関数\(Z\)も計算できることになります。統計物理学の研究においては自由エネルギーを計算することが重要になります(これさえ計算できれば論文が書ける?)。
統計物理で何か研究しようと思ったときには、エネルギーをモデル化することも重要です。そのエネルギーをもとに総和をとる or 積分を行うことで分配関数を計算することができますが、多変数においてはそれを計算することは困難を極めます。よって以下ではどのような式の形であれば総和・積分の計算ができるかを考えていきましょう。
人の手で解析的に計算可能な積分
有名なガウス積分
\[\int dx \ e^{-\frac{1}{2} a x^2} = \sqrt{\frac{2\pi}{a}} \tag{1.9}\] \[\sum_x e^{ax} = e^a + 1 \ (x = 0,1) \ {\rm or} \ 2 \cosh a \ (x=\pm 1) \tag{1.10}\]ならば計算できるでしょう。指数関数はガウス積分として、分数関数は等比級数になっていれば計算できます。とにかく、出てきた問題をこれらの形に変形するというのが重要なミッションになります。
どう頑張ってもこれらの形にできない問題は存在します。その場合は潔く諦めましょう。そこから新しい研究の種を見つけることが大切です。もしくは数値計算・数値シミュレーションを行うという方法もあります。その意味では「積分ができること」と「統計力学ができること」は等価と言っても良いでしょう。
多変数への一般化
上式を多変数に拡張しましょう。
\[\int d {\bf x} \ e^{-\frac{1}{2} {\bf x}^T A \bf{x}} = \sqrt{\frac{(2\pi)^N}{\rm{det}(A)}} \ (x \in \mathbb{R}^N) \tag{1.11}\] \[\sum_{\bf x} e^{\bf{a}^\top \cdot \bf{x}} = \sum_{\bf x} \prod_{i=1}^N e^{a_i x_i} = \prod_{i=1}^N \left( \sum_{x_i} e^{a_i x_i} \right) = \prod_{i=1}^N 2 \cosh a_i \ (x \in \{ -1, 1\}^N ) \tag{1.12}\]Ising model
これは磁性体を表現するためのトイモデルです。変数は2値 \(x = \pm 1\)のみを取ります。これはデジタル信号や情報処理への類推が可能です。\(N\)スピン系のこれは以下のような式で表されます。
\[E({\bf{x}}) = -J \sum x_i x_j - h \sum_i x_i \tag{1.13}\]ここで\(J\)とスピン同士の相互作用を表す係数、\(h\)は外磁場を表します。これは系のエネルギーを1次の項と2次の項とにテイラー展開した形と見ることもできます。
この系の振る舞いを以下に図示します。スピンが揃うとき、エネルギーは\(-J\)となり、系のエネルギーは下がります。一方でスピンが逆向きのとき、エネルギーは\(J\)となり、系のエネルギーが上がります。
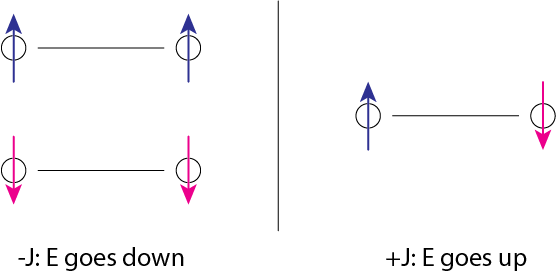
エネルギーは低い状態になろうとするので、全てのスピンは揃おうとします。しかしエントロピー\(S\)からは、温度を上げると状態の乱雑さが上昇し、向きが不揃いになるはずです。このことから低温から温度を徐々に上昇させると、スピンの向きが揃った状態から不揃いな状態に遷移する特別な温度の存在が示唆されます。
全結合モデル (Fushimi-Tempely model or Mean-Field model)
\[E({\bf{x}}) = -\frac{J}{2N} \sum_{i \neq j} x_i x_j \tag{1.14}\]この場合に計算を行っていきましょう。
\[Z = \sum_{\bf{x}} \exp \left( \frac{\beta J}{2N} \sum_{i \neq j} x_i x_j \right) \tag{1.15}\]ここで以下のテクニックを用います。
\[\sum_{i \neq j}^{N=3} x_{i} x_{j} = x_1 x_2 + x_2 x_3 + x_3 x_1 = \frac{1}{2} \{ (x_1 + x_2 + x_3)^2 - (x_1^2 + x_2^2 + x_3^2) \}\]です。添字の入れ替え\(x_2 x_1 + x_3 x_2 + x_1 x_3\)の場合も考えて、(1.15)式は
\[Z = \sum_{\bf{x}} \exp \left[ \frac{\beta J}{2N} \left\{ \left(\sum_i x_i \right)^2 - \sum_i x_i^2 \right\} \right]\]となります。ここで\(\sum_i x_i\)を\(\frac{1}{N} \sum_i x_i\)のように平均の形で見ることにしましょう。すると
\[Z = \sum_{\bf{x}} \exp \left\{ \frac{N \beta J}{2} \left( \frac{1}{N} \sum_i x_i\right)^2 - \frac{\beta J}{2}\right\}\]のようになります。途中、\(x_i \in \{ -1, 1\}\)より\(\sum_i x_i^2 = \sum_i 1 = N\)を用いました。
次に以下のテクニックを用います。
オンライン動画のTechnique 2の式と形が違うの注意が必要です。
(1.16)式は\(m = \frac{1}{N} \sum_i x_i\)を表しています。この\(m\)は磁化(Magnetization)を表します。
\[Z = N \sum_{\bf{x}} \int dm \ \exp \left( \frac{N\beta J}{2} m^2 - \frac{\beta J}{2} \right) \delta\left( Nm - \sum_i x_i\right)\]今、\(N \rightarrow \infty\)の極限を考えると、\(\exp (-\frac{\beta J}{2})\)の部分は無視して良いことがわかります。
\[Z = N \int dm \ \exp \left( N \frac{\beta J}{2} m^2 \right) \sum_{\bf{x}} \delta \left( N m - \sum_i x_i \right) \tag{1.17}\]エントロピーは状態数を数えたものです。状態数を数えるとは、同じエネルギーの状態を数えることを意味しますが、これは今では同じ磁化の状態を数えることに対応します(エネルギーが磁化にのみ依存していることからこのように考えられます)。するとデルタ関数部分はエントロピーを意味すると考えることができるので、以下のようにエントロピー\(S(m)\)を用いて
\[e^{N S(m)} = \sum_{\bf{x}} \delta \left( Nm - \sum_i x_i \right) \tag{1.18}\]のように定義することができます。そしてその前についているのはエネルギーで
\[e^{-\beta N e(m)} = \exp \left( N \frac{\beta J}{2} m^2 \right) \tag{1.19}\]と考えることができます。これらより
\[Z = N \int dm \ \exp [ N \{ -\beta e(m) + S(m)\} ] \tag{1.20}\]ここから自由エネルギーは
\[-\beta F = \log Z = \log \left( N \int dm \ \exp [ N\{ -\beta e(m) + S(m) \}] \right) \tag{1.21}\]この式に現れる被積分関数は\(\exp (N f(m))\)です。
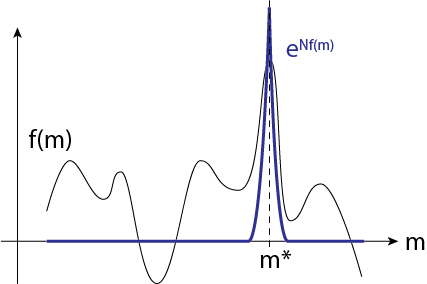
今は\(N \rightarrow \infty\)の場合を考えています。\(f(m)\)が最大となる部分で\(\exp (Nf(m))\)が極端に大きくなり、この場所の値だけが積分に寄与すると考えます。これを鞍点法(Saddle point method)と呼び、\(m = m^\ast\)のとき\(f(m)\)が最大であるとすると
\[\begin{align} -\beta F &= \log \left( N \exp [ N \{ -\beta e(m^\ast) + S(m^\ast)\} ] \right) \simeq \log \left( \exp [ N \{ -\beta e(m^\ast) + S(m^\ast)\} ] \right) \notag \\ &= -\beta N e(m^\ast) + N S(m^\ast) \tag{1.22} \end{align}\]これは熱力学でのヘルムホルツエネルギー\(F = U - TS\)を再現していることがわかります。途中、\(N = e^{\log N}\)は、\(N \rightarrow \infty\)においては\(e^{Nf(m)}\)に比べて無視できるとしました。
\(S(m)\)の計算
先ほどの計算からエントロピー\(S(m)\)は
\[S(m) = \frac{1}{N} \log \sum_{\bf{x}} \delta \left( Nm - \sum_i x_i \right) \tag{1.23}\]のように書かれました。この計算を進めるために、デルタ関数のフーリエ積分表示を考えましょう。
\[\delta \left( N m - \sum_i x_i \right) = \int d\tilde{m} \ \exp \left\{ -\tilde{m} \left( Nm - \sum_i x_i \right) \right\} \tag{1.24}\]\(\tilde{m}\)は本来であれば複素数\(ik\)と書くべきですが、ここでは鞍点法を用いるためこのように書いても不都合はありません。これらより
\[\begin{aligned} S(m) &= \frac{1}{N} \log \left[ \int d\tilde{m} \ \sum_{\bf{x}} \exp \left\{ -\tilde{m} \left(Nm - \sum_i x_i \right) \right\} \right] = \frac{1}{N} \log \left[ \int d\tilde{m} \ \exp (- N m \tilde{m}) \sum_{\bf{x}} \prod_{i=1}^N \exp (\tilde{m} x_i)\right] \\ &= \frac{1}{N} \log \left[ \int d\tilde{m} \exp (- N m \tilde{m}) (2 \cosh \tilde{m})^N \right] = \frac{1}{N} \log \left( \int d\tilde{m} \exp \left[ N \left\{ - m \tilde{m} + \log (2 \cosh \tilde{m}) \right\} \right] \right) \end{aligned}\]これにより、再び鞍点法を用いることができます。鞍点法は最大となる\(m = m^\ast\)の部分のみ積分に寄与するという考えなので、これを数式で表すと以下のようになります。
\[\int d\tilde{m} \ e^{N g(\tilde{m})} \simeq e^{Ng(\tilde{m}^\ast)} \ @ \ g' (\tilde{m}^\ast) = 0 \tag{1.25}\]今、\(g(\tilde{m}) = -m \tilde{m} + \log (2 \cosh \tilde{m})\)なので
\[g'(\tilde{m}) = - m + \tanh \tilde{m} = 0 \ \Longrightarrow \ \therefore \ m = \tanh \tilde{m} \tag{1.26}\]これらより
\[S(m) = \frac{1}{N} \log \exp \left[ N \left\{ - m \tilde{m}^\ast + \log (2 \cosh \tilde{m}^\ast ) \right\} \right] = - m \tilde{m}^\ast + \log (2\cosh \tilde{m}^\ast) \tag{1.27}\]これらを持ちいて自由エネルギーは
\[Z = \int dm \exp \left[ N \left\{ \frac{\beta J m^2}{2} - m \tilde{m} + \log(2\cosh \tilde{m})\right\} \right]\]となります。先ほどと同様の計算を行って
\[-\beta f(m) = \frac{\beta J m^2}{2} - m \tilde{m} + \log (2 \cosh \tilde{m}) \tag{1.28}\]これは1スピンあたりの自由エネルギーを表します。鞍点を計算すると
\[-\beta f'(m) = \beta J m - \tilde{m} = 0 \ \Longrightarrow \ \therefore \tilde{m} = \beta J m \tag{1.29}\](1.26), (1.29)式をまとめると
\[m = \tanh (\beta J m) \tag{1.30}\]となります。これは平均場近似を用いたときに出てきた自己無撞着方程式(Self-consistent equation)です。「平均場近似は所詮、近似手法に過ぎない」と思われたかもしれませんが、全結合においては厳密解を与える強力なツールとなっています。
物理では全結合の問題というのを考えるのは難しいかもしれません。しかし、情報科学においてはあるシグナルが他の様々n要素と関係づくことで機能することがあり得るため、物理的に繋がりを持っている必要はありません。よって全結合である問題をモデル化できるということが十分にあり得ます。
物理では\(N\)はアボガドロ数程度ですが、情報科学においては\(N \sim \mathcal{O}(100), \mathcal{O}(1000)\)です。これでも十分に統計力学が使えることが実験や数値計算で示されています。
有限の\(N\)の場合には、微小系の熱力学を考える必要があります。
(1.30)を図示して、この問題の振る舞いを見てみましょう。

逆温度\(\beta\)が大きいとき、(1.30)式の解の個数は3つです。しかし、\(\beta\)が小さいときは解の個数が1つになります。よって温度を変化させるとこの系の様子が劇的に変化する、相転移が見られることがわかります。
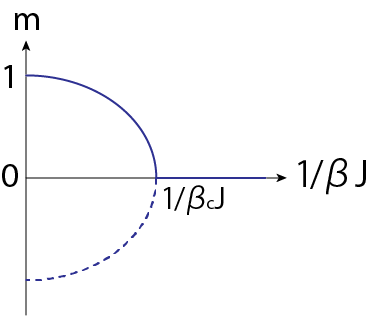
この相転移という現象は\(N\)が大きいときに現れるものです。もし\(N=2\)の場合、スピンの向きは平行か反平行の2つの状態のみで、相転移は見られません。\(N\)が大きいと協同現象・多体効果によって相転移がもたらされます。これは物理に限った話ではありません。
鞍点の安定性については、そこで取った値が最大(極大)なのか最小(極小)なのかを見極める必要があります。
Appendix: 多次元のガウス積分
\(N\)次元の正方正値対称行列\(A\)に対して
\[\int d\mathbf{x} e^{-\frac{1}{2} \mathbf{x}^\top A \mathbf{x}}\]を求めましょう。\(A\)が正の値しか持たない行列であることから、\(A^{1/2}\)が定義できます。よって\(e\)の肩を
\[\mathbf{x}^\top A \mathbf{x} = (A^{1/2} \mathbf{x})^\top (A^{1/2} \mathbf{x})\]のように変形します。\(\mathbf{y} = A^{1/2} \mathbf{x}\)とおくと、ヤコビアンは\(\mathrm{det} (A^{1/2})^{-1} = (\mathrm{det}(A))^{-1/2}\)です。よって
\[\int d\mathbf{x} e^{-\frac{1}{2} \mathbf{x}^\top A \mathbf{x}} = (\mathrm{det}(A))^{-1/2} \int d\mathbf{y} e^{-\frac{1}{2} (y_1^2 + y_2^2 + \cdots + y_n^2)} = \sqrt{\frac{(2\pi)^n}{\mathrm{det}(A)}}\]となります。
参考文献
[1] 大関真之 Youtube動画 “Statistical physics and information processing vol. 1 (情報統計物理) 【Tokyo Tech Lecture Live Streaming”
[2] 田崎晴明, “統計力学 I”
[3] 田崎晴明, “統計力学 II”
[4] 久保亮五, “大学演習 熱学・統計力学”
[5] 西森秀稔, “スピングラス理論と情報統計力学”