Table of contents
1.1 光のIntensityとFlux
光によるエネルギーの流れを表す量として、Intensity(Brightnessと呼ばれることもあります)とFluxとがあります。 両者とも、単位時間・単位面積あたりに通過するエネルギーのことですが、Intensityはある方向に進む光によって(その方向と垂直な単位面積当たりに)運ばれるエネルギーを表します。 一方、Flux \(F\)はあらゆる方向からくる光によって差し引き単位面積当たりに毎秒通過するエネルギーを表します。光のIntensityを\(I(\theta, \phi)\)、Fluxを\(F\)と記述すると、両者の関係は
\[F = \oint_{4\pi} I (\theta, \phi) \cos \theta d\Omega \tag{1.1}\]Intensityが\(\phi\)に依存しない場合は
\[F = \int_0^{2\pi} d\phi \int_0^\pi d\theta I (\theta) \cos \theta \sin \theta = 2\pi \int_0^\pi I (\theta) \cos \theta \sin \theta d\theta \tag{1.1'}\]のようになります。ここで、\(\theta\)は考えている面の垂直方向と光の進方向とのなす角を表し、\(d\Omega\)はその方向の周りの微小立体角を表します。Intensityに\(\cos \theta\)をかけて積分するのは、\(\theta\)の角度で単位面積を通過する光に垂直な面積が\(\cos \theta\)となるからです。
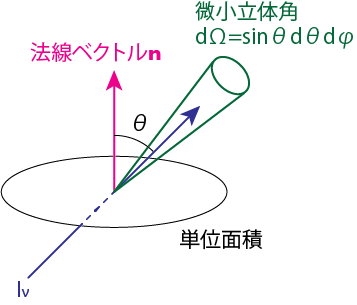
光のIntensity, Fluxはある振動数(の単位振動するあたり)のエネルギーを表す場合は添字をつけて\(I_\nu, F_\nu\)のように記述します。波長で表す場合には\(I_\lambda, F_\lambda\)です。
恒星
恒星の表面からは、外側に向かうあらゆる方向に光が発せられていますが、太陽以外の恒星は点光源として観測されます。そのため、ある方向にだけ発せられた光しか我々に届きません。
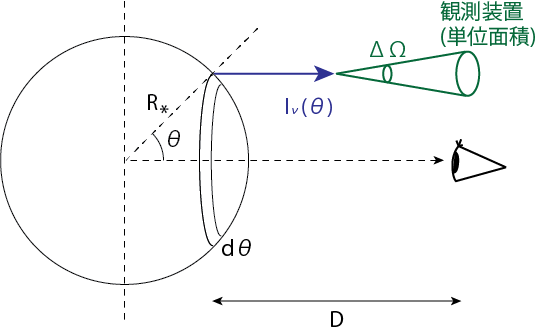
上図より、我々が一つの恒星から単位面積当たり単位時間に受け取るエネルギーは、微小面積\(R_\ast^2 \sin \theta d\theta d\phi\)から受け取るエネルギーを積分して
\[f_\nu = (\Delta \Omega) R_\ast^2 \int_0^{2\pi} d\phi \int_0^{\pi/2} I_\nu (\theta) \cos \theta \sin \theta d\theta d\phi \tag{1.2}\]と書けることがわかります。ここで\(R_\ast\)は星の半径、そして\(R_\ast^2 \sin \theta d\theta d\phi\)は星表面での微小面積を表します。また\(\Delta \Omega\)はその星から地上の単位面積を見たときの立体角です。その恒星までの距離を\(D\)とすると, \(\Delta \Omega = 1/D^2\)より
\[f_\nu = \left( \frac{R_\ast}{D}\right)^2 F_\nu \tag{1.3}\] \[F_\nu = 2\pi \int_0^\pi I_\nu (\theta) \cos \theta \sin \theta d \theta \ ({\rm 星の表面のRadiation \ flux})\]と書くことができます。 (星の表面では内向きに向かう光が無いと考えて\(I(\theta) = 0 \ ({\rm for} \ \pi/2 < \theta < \pi)\))。 この式より点光源として観測される恒星の光は、星の表面からのFluxを観測しており、地球で受け取る光のエネルギーは距離の2乗に反比例することを表しています。また、星の角半径
\[\alpha_\ast \equiv R_\ast /D\]およびLuminosity
\[L_\nu \equiv 4\pi R_\ast^2 F_\nu\]を定義します。すると(1.3)式は
\[f_\nu = \alpha_\ast^2 F_\nu = \frac{L_\nu}{4\pi D^2} \tag{1.3'}\]のように表現することもできます。
太陽や銀河のように広がりがある天体
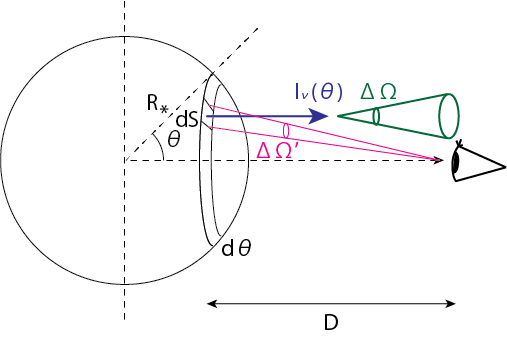
一方、太陽や銀河のように大きさの見える天体からの光の場合には事情が異なります。先ほどの図で、視線方向を軸とした球座標において\((R_\ast, \theta, \phi)\)の位置の単位面積から地球の単位面積に毎秒届く光のエネルギーは、地上の単位面積を見込む立体角を\(\Delta \Omega\)と書くと
\[(\Delta \Omega) I_\nu (\theta) \cos \theta \underbrace{R_\ast^2 \sin \theta d\theta d\phi}_{dS} = E_\nu (\theta) \Delta \Omega' \tag{1.4}\]のようになります。ここで\(E_\nu (\theta)\)は太陽方向と垂直な単位面積が、太陽面の\((R_\ast, \theta, \phi)\)単位面積から受け取るエネルギーを表します。そして\(\Delta \Omega'\)はそれを見込む立体角です。それぞれの立体角は
\[\Delta \Omega = \frac{1}{D^2}, \ \Delta \Omega' = \frac{dS \cos \theta}{D^2} \tag{1.5}\]より
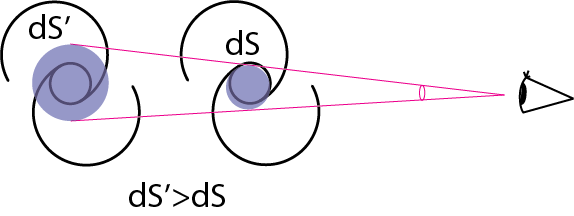
\[E_\nu (\theta) = I_\nu (\theta) \tag{1.6}\]となります。よってこの場合は光のIntenityを観測することになります。この場合、地上で観測する単位立体角あたりの明るさ(brightness)は距離に依存しません。これは距離が遠くなると、単位立体角に入ってくる天体の面積が距離の2乗に比例して広くなっているため、距離が遠くなると暗くなる効果と相殺するためです。
参考文献
[1] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”
[2] 梅村雅之, 福江純, 野村英子, “輻射輸送と輻射流体力学”
[3] Rybicki & Lightman, “Radiative Processes in Astrophysics”