Table of contents
逆コンプトン散乱の放射強度スペクトル
ここでは電磁波が相対論的速度で運動する電子から逆コンプトン散乱を受けたことによる、放射強度のスペクトルを求めてみましょう。入射電磁波の電磁場により引き起こされる電子の運動を輻射場のフーリエスペクトル式に代入することで、スペクトルを求めることができます。 散乱前の電子は\(z\)方向にのみ運動しており、その速度ベクトルは\(\boldsymbol{\beta}_0 = (0, 0, \beta_0)\)のように書きます。よって散乱前の電子の軌道は\(\mathbf{r}_0 (t') = (0, 0, \beta_0 c t')\)のように書けます。 視線方向\(\mathbf{n}\)を\(yz\)平面内にとり\(\mathbf{n} = (0, \sin \theta, \cos \theta)\)と表現します。入射電磁波の角振動数は\(\omega_0\)、波数ベクトルを\(\mathbf{k}_0 = k_0(\sin \theta_k \cos \varphi_k, \sin\theta_k \sin \varphi_k, \cos \theta_k)\)のように現しましょう。真空中の電磁波の分散関係式から、\(\omega_0 = k_0 c\)は常に満たされているとします。
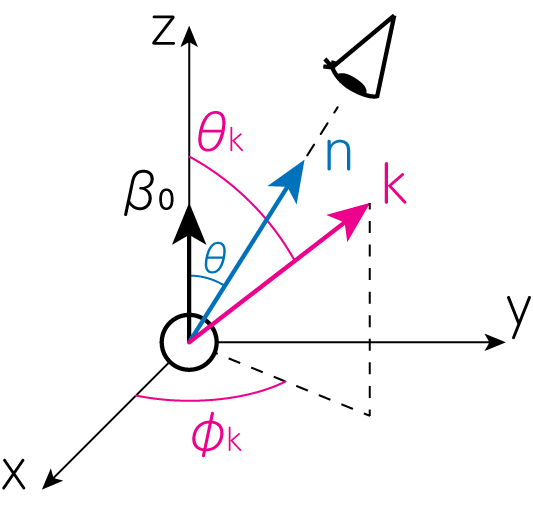
偏光ベクトルの向き
入射電磁波を、偏光ベクトルが\(\boldsymbol{\beta}_0-\mathbf{k}\)平面内にある\(\boldsymbol{\epsilon}_1\)の成分と、この平面に直交する\(\boldsymbol{\epsilon}_2\)の成分の2つの成分に分解し、以下の解析を行いましょう。そのために、まずこの2つの偏光ベクトルの向きを求めます。 \(\boldsymbol{\epsilon}_1\)は\({\bf e}_z\)を\(x\)軸回りに\(-(\frac{\pi}{2} + \theta_k)\)回転したのちに、\(z\)軸回りに\(-(\frac{\pi}{2}-\varphi_k)\)回転することで得られます。
\[\boldsymbol{\epsilon}_1 = \left( \begin{array}{ccc} \cos (-(\frac{\pi}{2} -\varphi_k)) & - \sin (-(\frac{\pi}{2} -\varphi_k)) & 0 \\ \sin (-(\frac{\pi}{2} -\varphi_k)) & \cos (-(\frac{\pi}{2} -\varphi_k)) & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (-(\frac{\pi}{2} +\theta_k)) & - \sin (-(\frac{\pi}{2} +\theta_k)) \\ 0 & \sin (-(\frac{\pi}{2} +\theta_k)) & \cos (-(\frac{\pi}{2} +\theta_k)) \end{array} \right) \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} \cos \varphi_k \cos \theta_k \\ \sin \varphi_k \cos \theta_k \\ -\sin \theta_k \end{array} \right)\]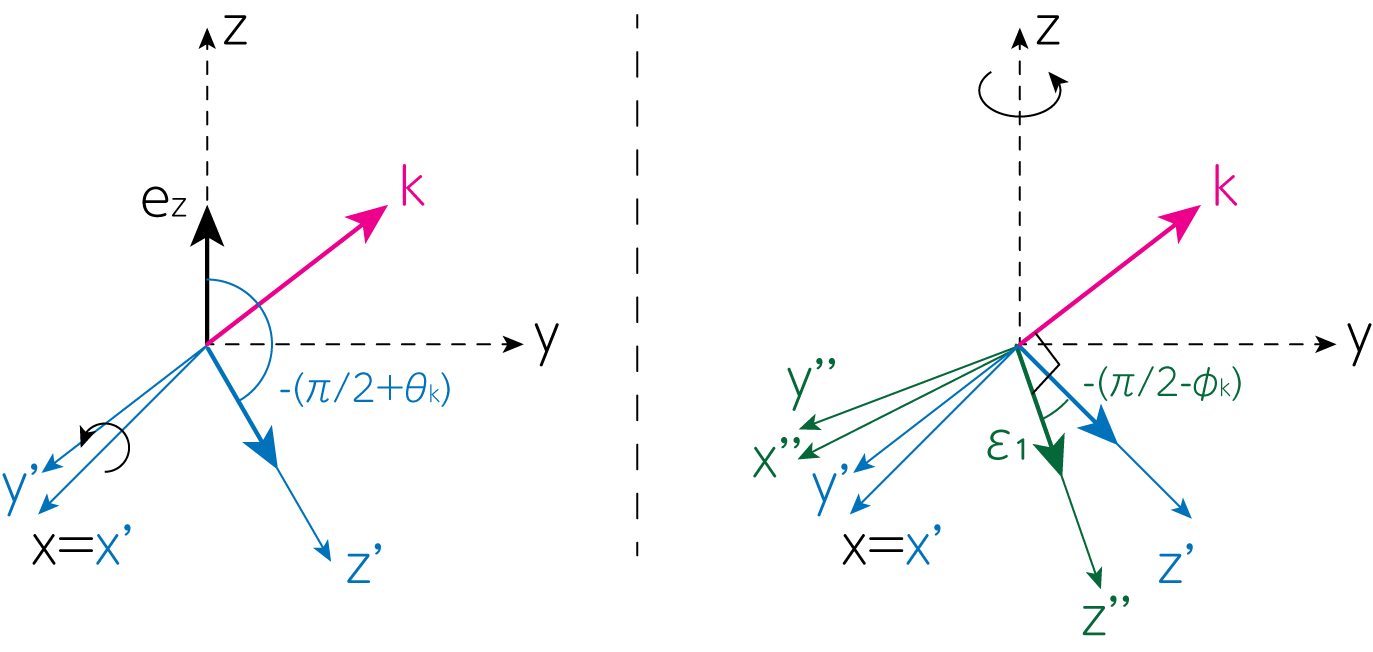
上図左パネルは\(z\)軸周りに回転する変換、右パネルは\(x\)軸周りに回転する変換です。次に、\(\boldsymbol{\epsilon}_2\)は\({\bf e}_y\)を\(z\)軸回りに\(\varphi_k\)回転することで得られます。
\[\boldsymbol{\epsilon}_2 = \left( \begin{array}{c} -\sin \varphi_k \\ \cos \varphi_k \\ 0 \end{array} \right)\]このようにすることで、\(\boldsymbol{\beta}_0-\mathbf{k}\)平面内にありながら\(\mathbf{k} \perp \boldsymbol{\epsilon}_1\)を満たす偏光ベクトル\(\boldsymbol{\epsilon}_1\)と、\(\boldsymbol{\epsilon}_1, \mathbf{k}\)の両方に直交する偏光ベクトル\(\boldsymbol{\epsilon}_2\)を定めることができます。
3次元の回転を2次元紙面上で描くの無理ゲーすぎる...そのうち3DCGを用いた説明図を掲載予定です。
必要であれば、自分でペンを3本持って実際に回転させるのもありかもしれません。
電子の運動方程式
それでは計算を進めていきましょう。まずは電子の運動方程式からです。電磁場中の荷電粒子の運動方程式より、エネルギーの時間変化は
\[\frac{d}{dt} (\gamma m_e c^2) = -e {\bf E} \cdot {\bf v} \ \Longrightarrow \ \frac{d\gamma}{dt} = -\frac{e}{m_e c^2} {\bf E} \cdot {\bf v}\]のように書かれます。次に運動量変化の式は
\[\frac{d}{dt} (\gamma m_e {\bf v}) = -e ({\bf E} + \frac{\bf v}{c} \times {\bf B}) \ \Longrightarrow \ m_e \gamma \frac{d {\bf v}}{dt} + m_e {\bf v} \frac{d\gamma}{dt} = -e ({\bf E} + \frac{\bf v}{c} \times {\bf B})\]です。先ほどの式を代入して
\[m_e c \gamma \frac{d \boldsymbol{\beta}}{dt} = e({\bf E} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} - e{\bf E} - c \boldsymbol{\beta} \times {\bf B} \ \Longrightarrow \ \frac{d\boldsymbol{\beta}}{dt} = \frac{e}{m_e c\gamma} (({\bf E} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} - {\bf E} - \boldsymbol{\beta} \times {\bf B}) \tag{1}\]のように、電子の速度変化を表す式が得られます。
まずは入射電磁波が\(\boldsymbol{\epsilon}_1\)方向に直線偏光している場合を考えましょう。このとき、電磁場はそれぞれ
のように記述されます。ここで\(E=B, \omega_0 = k_0 c\)です。また電磁波の位相の中に現れる電子の軌道を、観測者から天体までの距離が十分遠いとして\({\bf r}_0 (t') \simeq {\bf r} (t')\)とします。これは
\[{\bf k}_0 \cdot {\bf r}(t') \simeq {\bf k}_0 \cdot {\bf r}_0 (t') = k_0 \beta ct' \cos \theta_k\]より
\[\omega_0 t' - {\bf k}_0 \cdot {\bf r} (t') = \omega_0 t' (1-\beta \cos \theta_k) = \tilde{\omega}_0 t'\]としたとき、\(\omega_{\rm se} / \tilde{\omega}_0 \ll 1\)で有る限り良い精度の近似になっています(詳細は後述)。ここで\(\omega_{\rm se} \equiv eE/(\gamma m_e c)\)はシンクロトロン振動数です。電場・磁場の成分を具体的に書き下すと
\[{\bf E} = E \sin (\omega_0 t' (1-\beta \cos \theta_k)) \boldsymbol{\epsilon}_1 = E \sin \tilde{\omega}_0 t' \left( \begin{array}{c} \cos \theta_k \cos \varphi_k \\ \cos \theta_k \sin \varphi_k \\ - \sin \theta_k \end{array} \right)\] \[{\bf B} = E \sin (\omega_0 t' (1-\beta \cos \theta_k)) \boldsymbol{\epsilon}_2 = E \sin \tilde{\omega}_0 t' \left( \begin{array}{c} - \sin \varphi_k \\ \cos \varphi_k \\ 0 \end{array} \right)\]です。さらに(1)式の計算のために以下のものを計算します。
\[(\boldsymbol{\epsilon}_1 \cdot \boldsymbol{\beta} ) \boldsymbol{\beta} = -\sin \theta_k \beta_0 \boldsymbol{\beta} = - \beta_0^2 \sin \theta_k {\bf e}_z\] \[\boldsymbol{\beta} \times {\bf B} \propto \boldsymbol{\beta} \times \boldsymbol{\epsilon}_2 = \beta_0 \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \times \left( \begin{array}{c} -\sin \varphi_k \\ \cos \varphi_k \\ 0 \end{array} \right) = \beta_0 \left( \begin{array}{c} -\cos \varphi_k \\ -\sin \varphi_k \\ 0 \end{array} \right)\]以上より
\[\begin{aligned} \frac{d \boldsymbol{\beta}}{dt} &= \frac{e}{m_e c \gamma} (-\beta_0^2 \sin \theta_k E \sin \tilde{\omega} t' ) {\bf e}_z - \frac{e}{m_e c \gamma} E \sin \tilde{\omega}_0 t' \left( \begin{array}{c} \cos \theta_k \cos \varphi_k \\ \cos \theta_k \sin \varphi_k \\ - \sin \theta_k \end{array} \right) - \frac{e}{m_e c \gamma} E \sin \tilde{\omega} t' \beta_0 \left( \begin{array}{c} - \cos \varphi_k \\ - \sin \varphi_k \\ 0 \end{array} \right) \\ &= \omega_{\rm se} \sin \tilde{\omega}_0 t' \left( \begin{array}{c} \beta_0 \cos \varphi_k - \cos \theta_k \cos \varphi_k \\ \beta_9 \sin \varphi_k - \cos \theta_k \sin \varphi_k \\ \sin \theta_k - \beta_0^2 \sin \theta_k \end{array} \right) = \omega_{\rm se} \sin \tilde{\omega}_0 t' \left( \begin{array}{c} (\beta_0 -\cos \theta_k) \cos \varphi_k \\ (\beta_0 - \cos \theta_k) \sin \varphi_k \\ \gamma^{-2} \sin \theta_k \end{array} \right) \end{aligned}\]すると電磁場により電子の速度および位置は
\[\boldsymbol{\beta} = \underbrace{\boldsymbol{\beta}_0}_{初期速度} + \int \frac{d \boldsymbol{\beta}}{dt'} dt' = \beta_0 {\bf e}_z -\frac{\omega_{\rm se}}{\tilde{\omega}_0} \cos \tilde{\omega} t' \left( \begin{array}{c} (\beta_0 -\cos \theta_k) \cos \varphi_k \\ (\beta_0 - \cos \theta_k) \sin \varphi_k \\ \gamma^{-2} \sin \theta_k \end{array} \right)\] \[{\bf r} =\underbrace{\bf 0}_{初期位置} + c \int \frac{d\boldsymbol{\beta}}{dt'} dt' \ \Longrightarrow \ \frac{\bf r}{c} = \left( \begin{array}{c} -\frac{\omega_{\rm se}}{\tilde{\omega}_0^2} \sin \tilde{\omega}_0 t' (\beta_0 - \cos \theta_k) \cos \varphi_k \\ -\frac{\omega_{\rm se}}{\tilde{\omega}_0^2} \sin \tilde{\omega}_0 t' (\beta_0 - \cos \theta_k) \sin \varphi_k \\ \beta_0 t' -\frac{\omega_{\rm se}}{\tilde{\omega}_0^2} \sin \tilde{\omega}_0 t' \gamma^{-2} \sin \theta_k \end{array} \right)\]のように変化します。
輻射場のフーリエスペクトル計算
輻射場のフーリエスペクトルを計算するために、以下の計算をおこないましょう。
\[[{\bf n} \times ({\bf n} \times \boldsymbol{\beta})]_i = \epsilon_{ijk} n_j \epsilon_{k\ell m} n_\ell \beta_m = \epsilon_{kij} \epsilon_{k \ell m} n_j n_\ell \beta_m = (\delta_{i\ell} \delta_{jm} - \delta_{im} \delta_{j\ell}) n_j n_\ell \beta_m = n_j n_i \beta_j - n_j n_j \beta_i = [({\bf n} \cdot \boldsymbol{\beta}) {\bf n} - \boldsymbol{\beta}]_i\] \[{\bf n} \cdot \boldsymbol{\beta} = \beta_0 \cos \theta + \frac{\omega_{\rm se}}{\tilde{\omega}_0 } \cos \tilde{\omega}_0 t' ((\cos \theta_k -\beta_0) \sin \theta \sin \varphi_k - \gamma^{-2} \cos \theta \sin \theta_k)\] \[[{\bf n} \times ({\bf n} \times \boldsymbol{\beta})]_x = -\frac{\omega_{\rm se}}{\tilde{\omega}_0} \cos \tilde{\omega}_0 t' (\cos \theta_k - \beta_0) \cos \varphi_k\] \[[{\bf n} \times ({\bf n} \times \boldsymbol{\beta})]_y = \frac{1}{2} \beta_0 \sin 2 \theta + \frac{\omega_{\rm se}}{\tilde{\omega}_0} \cos \tilde{\omega}_0 t' (-(\cos \theta_k -\beta_0) \sin \varphi_k \cos^2 \theta - \frac{\sin \theta_k}{2\gamma^2} \sin 2\theta)\] \[[{\bf n} \times ({\bf n} \times \boldsymbol{\beta})]_z = -\beta_0 \sin^2 \theta + \frac{\omega_{\rm se}}{\tilde{\omega}_0} \cos \tilde{\omega}_0 t' (\frac{1}{2} (\cos \theta_k -\beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta)\] \[t' - \frac{\bf{n} \cdot \bf{r}}{c} = (1-\beta_0 \cos \theta) t' + \frac{\omega_{\rm se}}{\tilde{\omega}_0^2} \sin \tilde{\omega}_0 t' (-\sin \theta (\cos \theta_k - \beta_0) \sin \varphi_k + \cos \theta \frac{\sin \theta_k}{\gamma^2})\] \[R \hat{\bf E}({\bf r}, \omega) = \frac{i e \omega}{2\pi c} e^{i\varphi} \int_{T'_1}^{T'_2} {\bf n} \times ({\bf n} \times \boldsymbol{\beta}) e^{i\omega (t' - \frac{\bf{n} \cdot \bf{r}}{c})} dt'\]よって電場の\(x\)成分に(後の計算のために)\(R\)をかけた量は
\[R \hat{E}_x ({\bf r}, \omega) = \frac{ie \omega}{2\pi c} e^{i\varphi} \int_{T'_1}^{T'_2} (-\frac{\omega_{\rm se}}{\tilde{\omega}_0}\cos \tilde{\omega}_0 t' (\cos \theta_k - \beta_0) \cos \varphi_k) e^{i (1-\beta_0 \cos \theta) \omega t'} e^{i \omega \frac{\omega_{\rm se}}{\tilde{\omega}_0^2} \sin \tilde{\omega}_0 t' (- \sin \theta (\cos \theta_k -\beta_0) \sin \varphi_k + \cos \theta \frac{\sin \theta_k}{\gamma^2})} dt'\]のようになります。以降、\(A \equiv \omega \frac{\omega_{\rm se}}{\tilde{\omega}_0^2} (-\sin \theta (\cos \theta_k - \beta_0) \sin \varphi_k + \cos \theta \frac{\sin \theta_k}{\gamma^2})\)とおきます。
\[R \hat{E}_x ({\bf r}, \omega) = \frac{ie \omega}{2\pi c} e^{i\varphi} \int_{T'_1}^{T'_2} (-\frac{\omega_{\rm se}}{\tilde{\omega}_0}\cos \tilde{\omega}_0 t' (\cos \theta_k - \beta_0) \cos \varphi_k) e^{i (1-\beta_0 \cos \theta) \omega t'} e^{i A \sin \tilde{\omega}_0 t'} dt'\]ここで
\[\frac{d}{dt'} e^{iA \sin \tilde{\omega}_0 t'} = i A \tilde{\omega}_0 \cos \tilde{\omega}_0 t' e^{iA \sin \tilde{\omega}_0 t'}\]のように計算されるので
\[\begin{aligned} R \hat{E}_x &= - \frac{ie\omega}{2\pi c} \frac{\omega_\mathrm{se}}{i A \tilde{\omega}_0^2} (\cos \theta_k -\beta_0) \cos \varphi_k e^{i\varphi} \int_{T_1'}^{T_2'} e^{i(1-\beta_0 \cos \theta) \omega t'} \frac{d}{dt'} e^{iA \sin \tilde{\omega}_0 t'} dt' \\ &= - \frac{ie\omega}{2\pi c} \frac{\omega_\mathrm{se}}{iA \tilde{\omega}_0^2} (\cos \theta_k - \beta_0) \cos \varphi_k e^{i\varphi} \left\{ \left[ e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} \right]_{T_1'}^{T_2'} - \int_{T_1'}^{T_2'} i(1-\beta_0 \cos \theta) \omega e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'}\right\} \end{aligned}\]この積分において長時間平均を取ると、\([\cdots]_{T_1'}^{T_2'}\)の項は無視できて
\[R \hat{E}_x = \frac{ie\omega^2 \omega_\mathrm{se}}{2\pi c A \tilde{\omega}^2} (\cos \theta_k - \beta_0) (1-\beta_0 \cos \theta) \cos \varphi_k e^{i\varphi} \int_{T_1'}^{T_2'} e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} dt'\]のように書けます。ここでベッセル関数を考えているときに現れたフーリエ級数展開より
\[e^{iA \sin \tilde{\omega} t'} = \sum_{n=-\infty}^\infty J_n (A) e^{in \tilde{\omega}_0 t'}\]と書かれるので
\[\begin{aligned} R \hat{E}_x &= \frac{ie \omega^2 \omega_\mathrm{se}}{2\pi c A \tilde{\omega}_0^2} (\cos \theta_k-\beta_0) (1-\beta_0 \cos \theta) \cos \varphi_k e^{i\varphi} \sum_{n=-\infty}^\infty J_n(A) \int_{T_1'}^{T_2'} e^{i\{(1-\beta_0 \cos \theta) \omega + n\tilde{\omega}_0\} t'} dt' \\ &\underbrace{=}_{T_2' = - T_1' = T'/2} \frac{ie \omega^2 \omega_\mathrm{se}}{2\pi c A \tilde{\omega}_0^2} (\cos \theta_k-\beta_0) (1-\beta_0 \cos \theta) \cos \varphi_k e^{i\varphi} \sum_{n=-\infty}^\infty J_n(A) \frac{2 \sin \left[ \{(1-\beta_0 \cos \theta) \omega + n \tilde{\omega}_0\} \frac{T'}{2} \right]}{(1-\beta_0 \cos \theta) \omega + n \tilde{\omega}_0} \\ &= \frac{ie \omega^2 \omega_\mathrm{se}}{2\pi c A \tilde{\omega}_0^2} (\cos \theta_k-\beta_0) (1-\beta_0 \cos \theta) \cos \varphi_k e^{i\varphi} \sum_{n=-\infty}^\infty J_n(A) T' \mathrm{sinc} \left[ \{(1-\beta_0 \cos \theta) \omega + n \tilde{\omega}_0\} \frac{T'}{2} \right] \end{aligned}\]今、\(A \ll 1\)を考えましょう(これが正しいことは後述します)。よってベッセル関数を\(J_n(A) \simeq J_n(0) + J_n'(0) A\)のようにテイラー展開すると
するとベッセル関数の定義より
\[J_n (A) = \frac{1}{\pi} \int_0^\pi \cos (n\varphi - A \sin \varphi) d\varphi \simeq \frac{1}{\pi} \int_{0}^\pi \cos n\varphi d\varphi\] \[J_n'(A) = \frac{1}{\pi} \int_0^\pi \{ -\sin (n\varphi - A \sin \varphi) \}-\sin\varphi d\varphi\simeq \frac{1}{\pi} \int_0^\pi \sin n \varphi \sin \varphi\]と計算されるので
\[\begin{aligned} &J_0(A) = J_0 (0) + J_0'(0) A = J_0 = 1 \\ &J_1(A) = J_1(0) + J_1'(0) A = J_1'(0) A = \frac{1}{2} A \\ &J_n(0) = J_n'(0) = 0 \quad (n \geq 2) \\ &J_{-1}(A) = - J_1 (A) \simeq -\frac{1}{2} A \end{aligned}\]などが求まります。この計算からは\(J_0(A) = 1\)が大きな寄与をしそうな気がします。しかしその場合、sinc関数の性質から\(\omega=0\)が\(R\hat{E}\)のピークとなりそうですが、そもそも\(R \hat{E} \propto \omega^2\)です。よって\(n=0\)からの寄与はゼロとなることがわかります。 以上の議論から、ゼロでない有限の値を持つ最低次は\(n=\pm 1\)であるとわかります。実際には\(n < 0\)でなければ\(\omega > 0\)の領域でピークを持つようなsinc関数を得られないため、\(n = -1\)を採用します。すると
\[R\hat{E}_x = -\frac{ie \omega^2 \omega_\mathrm{se}}{4\pi c \tilde{\omega}_0^2} (\cos \theta_k-\beta_0) (1-\beta_0 \cos \theta) \cos \varphi_k e^{i\varphi}T' \mathrm{sinc} \left[ \{(1-\beta_0 \cos \theta) \omega - \tilde{\omega}_0\} \frac{T'}{2} \right] \tag{5}\]となります。同様に\(R\hat{E}_y, R\hat{E}_z\)を計算していきましょう。
\[\begin{aligned} R \hat{E}_y (\mathbf{r}, \omega) &= \frac{i e\omega}{2\pi e} e^{i\varphi} \int_{-T'/2}^{T'/2} \left[ \frac{1}{2} \beta_0 \sin 2\theta + \frac{\omega_\mathrm{se}}{\tilde{\omega}_0} \cos \tilde{\omega}_0 t' \left\{ -(\cos \theta_k - \beta_0) \sin \varphi_k \cos^2 \theta -\frac{\sin \theta_k}{2\gamma^2} \sin 2\theta \right\} \right] e^{iA \sin \tilde{\omega}_0 t'} e^{i(1-\beta_0 \cos \theta) \omega t'} dt' \\ &= \frac{i e\omega}{4\pi e} e^{i\varphi} \int_{-T'/2}^{T'/2} \beta_0 \sin 2\theta e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} dt' \\ & \qquad - \frac{ie\omega}{2\pi c} e^{i\varphi} \left\{ (\cos \theta_k - \beta_0) \sin \varphi_k \cos^2 \theta + \frac{\sin \theta_k}{2\gamma^2} \sin 2\theta \right\} \frac{\omega_\mathrm{se}}{\tilde{\omega}} \int_{-T'/2}^{T'/2} \underbrace{\cos \tilde{\omega}_0 t' e^{iA \sin \tilde{\omega}_0 t'}}_{=\frac{1}{iA \tilde{\omega}_0} \frac{d}{dt} e^{iA \sin \tilde{\omega}_0 t'}} e^{i(1-\beta_0 \cos \theta) \omega t'} dt' \\ &= \frac{i e\omega}{4\pi e} e^{i\varphi} \int_{-T'/2}^{T'/2} \beta_0 \sin 2\theta e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} dt' \\ & \qquad - \frac{e\omega}{2\pi c} e^{i\varphi} \left\{ (\cos \theta_k - \beta_0) \sin \varphi_k \cos^2 \theta + \frac{\sin \theta_k}{2\gamma^2} \sin 2\theta\right\} \frac{\omega_\mathrm{se}}{\tilde{\omega}_0} \\ & \qquad \quad \times \frac{1}{A \tilde{\omega}_0} \left( \left[ e^{iA \sin \tilde{\omega}_0 t'} e^{i(1-\beta_0 \cos \theta) \omega t'} \right]_{-T'/2}^{T'/2} - i(1-\beta_0 \cos \theta) \omega \int_{-T'/2}^{T'/2} e^{iA \sin \tilde{\omega}_0 t'} e^{i(1-\beta_0 \cos \theta) \omega t'} dt'\right) \end{aligned}\]\(R\hat{E}_x\)の計算と同じく、長時間平均とベッセル関数のフーリエ変換で現れる公式、そして\(n=-1\)が支配的であることを用いると
\[\begin{align} R \hat{E}_y &= \frac{ie \omega}{4\pi c} e^{i\varphi} \beta_0 \sin 2\theta \int_{-T'/2}^{T'/2} e^{i(1-\beta_0 \cos \theta) \omega t'} \sum_{n=-\infty}^\infty J_n (A) e^{in\tilde{\omega}_0 t'} dt' \notag \\ & \qquad + \frac{e\omega}{2\pi c} e^{i\varphi} \frac{\omega_\mathrm{se}}{A \tilde{\omega}_0^2} \left\{ (\cos \theta_k -\beta_0) \sin \varphi_k \cos^2 \theta + \frac{\sin \theta_k}{2 \gamma^2} \sin 2\theta \right\} i (1-\beta_0 \cos \theta) \omega \int_{-T'/2}^{T'/2} e^{i(1-\beta_0 \cos \theta) \omega t'} \sum_{n=-\infty}^\infty J_n(A) e^{in\tilde{\omega}_0 t'}dt' \notag \\ &= \frac{ie\omega}{2\pi c} e^{i\varphi} \left[ \frac{\beta_0}{2} \sin 2\theta + \frac{\omega_\mathrm{se}}{A \tilde{\omega}_0^2} \left\{ (\cos \theta_k - \beta_0) \sin \varphi_k \cos^2 \theta + \frac{\sin \theta_k}{2\gamma^2} \sin 2\theta \right\} (1-\beta_0 \cos \theta) \omega \right] \notag \\ & \qquad \times T' \left( -\frac{A}{2} \right) \mathrm{sinc} \left[ \{ (1-\beta_0 \cos \theta) \omega -\tilde{\omega}_0\} \frac{T'}{2} \right] \notag \\ &\underbrace{=}_{Aを代入} -\frac{ie e^{i\varphi}}{4\pi c} \frac{\omega^2 \omega_\mathrm{se}}{\tilde{\omega}_0^2} \left\{ \cos \theta (\cos \theta -\beta_0) (\cos \theta_k - \beta_0) \sin \varphi_k + \frac{\sin \theta_k}{2\gamma^2} \sin 2\theta \right\} T' \mathrm{sinc} \left[ \{ (1-\beta_0 \cos \theta) \omega -\tilde{\omega}_0\} \frac{T'}{2} \right] \tag{6} \end{align}\]続いて\(R \hat{E}_z\)の計算です。これまでと同じく、長時間平均とベッセル関数のフーリエ変換で現れる公式、そして\(n = -1\)が支配的であることを用いて
\[\begin{align} R \hat{E}_z (\mathbf{r}, \omega) &= \frac{ie\omega}{2\pi c} e^{i\varphi} \int_{-T'/2}^{T'/2} \left[ -\beta_0 \sin^2 \theta + \frac{\omega_\mathrm{se}}{\tilde{\omega}_0} \cos \tilde{\omega}_0 t' \left\{ \frac{1}{2} (\cos \theta_k - \beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\}\right] e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} dt' \notag \\ &= \frac{ie\omega}{2\pi c} e^{i\varphi} \int_{-T'/2}^{T'/2} (-\beta_0 \sin^2 \theta) e^{i(1-\beta_0 \cos \theta) \omega t'} e^{iA \sin \tilde{\omega}_0 t'} dt' \notag \\ & \qquad + \frac{ie \omega}{2\pi c}e^{i\varphi} \frac{\omega_\mathrm{se}}{\tilde{\omega}_0} \left\{ \frac{1}{2} (\cos \theta_k - \beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\} \int_{-T'/2}^{T'/2} \underbrace{\cos \tilde{\omega}_0 t' e^{iA \sin \tilde{\omega}_0 t'}}_{=\frac{1}{iA\tilde{\omega}_0} \frac{d}{dt'} e^{iA \sin \tilde{\omega}_0 t'}} e^{i(1-\beta_0 \cos \theta) \omega t'} dt' \notag \\ &= \frac{ie \omega}{2\pi c} e^{i\varphi} (-\beta_0 \sin^2 \theta) \int_{-T'/2}^{T'/2} e^{i(1-\beta_0 \cos \theta) \omega t'} \sum_{n=-\infty}^\infty J_n(A) e^{in\tilde{\omega}_0 t'} dt' \notag \\ & \qquad + \frac{ie \omega}{2\pi c} e^{i\varphi} \frac{\omega_\mathrm{se}}{\tilde{\omega}_0} \left\{ \frac{1}{2} (\cos \theta_k - \beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\} \frac{-1}{iA \tilde{\omega}_0} \int_{-T'/2}^{T'/2} i (1-\beta_0 \cos \theta) \omega e^{i(1-\beta_0 \cos \theta) \omega t'} \sum_{n=-\infty}^\infty J_n (A) e^{in \tilde{\omega}_0 t'} dt' \notag \\ &= - \frac{ie\omega}{2\pi c} e^{i\varphi} \left[ \beta_0 \sin^2 \theta + \frac{\omega_\mathrm{se} \omega}{\tilde{\omega}_0^2 A} \left\{ \frac{1}{2} (\cos \theta_k - \beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\} (1-\beta_0 \cos \theta) \right] \sum_{n=-\infty}^\infty J_n(A) T' \mathrm{sinc} \left[\{ (1-\beta_0 \cos \theta) \omega + n\tilde{\omega} \} \frac{T'}{2} \right] \notag \\ &\underbrace{=}_{n = -1} \frac{ie\omega}{4\pi c} e^{i\varphi} \left[ A \beta_0 \sin^2 \theta + \frac{\omega_\mathrm{se} \omega}{\tilde{\omega}_0^2} \left\{ \frac{1}{2} (\cos \theta_k - \beta_0) \sin 2\theta \sin \varphi_k + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\} (1-\beta_0 \cos \theta) \right] \ T' \mathrm{sinc} \left[\{ (1-\beta_0 \cos \theta) \omega -\tilde{\omega} \} \frac{T'}{2} \right] \notag \\ & \underbrace{=}_{Aを代入} \frac{ie \omega}{4\pi c} e^{i\varphi} \frac{\omega_\mathrm{se} \omega}{\tilde{\omega}_0^2} \left\{ (\cos \theta_k - \beta_0) \sin \varphi_k \sin \theta (\cos \theta -\beta_0) + \frac{\sin \theta_k}{\gamma^2} \sin^2 \theta \right\} T' \tag{7} \end{align}\](5), (6), (7)式より、この放射は\(\omega = \frac{\tilde{\omega}_0}{1-\beta_0 \cos\theta} = \frac{1-\beta_0 \cos \theta_k}{1-\beta_0 \cos \theta} \omega_0\)に集中することがわかります。これは
\[\omega \gamma (1-\beta_0 \cos \theta) = \omega_0 \gamma (1-\beta_0 \cos \theta_k) \tag{8}\]のように変形できます。左辺は散乱された放射の周波数を電子静止系にローレンツ変換したもの、右辺は入射してきた放射の周波数を電子静止系にローレンツ変換したものです。つまり、電子静止系では入射放射と散乱放射の周波数が変化しません。言い換えれば、散乱前後で光子のエネルギーが変化しないことを表しています。これは\(n = -1\)だけを採用する近似がトムソン散乱極限に対応していることを意味します。
先程の\(A \ll 1\)が正しいかどうかを検証しましょう。
\[\frac{\omega_\mathrm{se} \omega}{\tilde{\omega}_0^2} \simeq \frac{\gamma^2 \omega_0}{\omega_0^2} \frac{eB}{\gamma m_e c} = \frac{eB}{m_e c} \frac{\gamma}{\omega_0} = \sqrt{\frac{e^2 B^2}{m_e^2 c^2} \frac{\gamma^2}{\omega_0^2}} = \sqrt{\frac{e^2 B^2}{m_e c} \frac{\gamma^2}{\omega_0^2} \frac{h}{m_e c} \frac{1}{h}} = \sqrt{\frac{e^2}{m_e c^2} c B^2 \frac{\gamma^2}{\omega_0^2} \frac{1}{h} \lambda_c}\]途中、コンプトン波長\(\lambda_c = \frac{h}{m_e c}\)を用いました。さらに式の途中の\(cB^2\)はポインティングベクトルの振幅であり、これは入射電磁場の輻射強度と\(I_\nu d\nu \simeq \nu I_\nu \ (d\nu \simeq \nu)\)の関係があります。逆コンプトン散乱を受ける放射としてCMB(黒体放射のレイリー・ジーンズ極限)を考えると
\[\frac{\omega_\mathrm{se} \omega}{\tilde{\omega}_0^2} \simeq \sqrt{\frac{e^2}{m_e c^2} \frac{2k_B T}{c^2} \nu_0^3 \frac{\gamma^2}{\omega_0^2} \frac{1}{h} \lambda_c} \underbrace{=}_{\omega_0 = 2\pi \nu_0, c = \nu_0 \lambda_0} \sqrt{\frac{e^2}{m_e c^2} \frac{2k_B T}{c} \frac{1}{(2\pi)^2}\frac{1}{h} \frac{\lambda_c}{\lambda_0 / \gamma^2}} = \sqrt{\frac{e^2}{\hbar c} \frac{\lambda_c}{\lambda_0/\gamma^2} \frac{2}{(2\pi)^3} \frac{k_B T}{m_e c^2} }\]のように変形されます。\(\frac{e^2}{\hbar c} \sim \frac{1}{137}\)は微細構造定数、そして\(\lambda_0 / \gamma^2\)は散乱後の電磁波の波長を表します。よってこの式は、散乱後の波長が電子のコンプトン波長よりも十分長く、入射電磁波の放射温度が電子質量より十分小さければ、\(A \ll 1\)のような取り扱いができることを示しています。さらに\(\frac{\omega \omega_\mathrm{se}}{\tilde{\omega}_0^2} \simeq \frac{\gamma^2 \omega_\mathrm{se}}{\tilde{\omega}_0}\)なので、上式が満たされていれば必ず\(\frac{\omega_\mathrm{se}}{\tilde{\omega}} \ll 1\)が満たされることになります。よって、最初に運動方程式を\(\omega_\mathrm{se}/ \tilde{\omega}_0\)のオーダーで摂動展開して求めたことの正当性も保証されていることがわかります。
逆コンプトン散乱放射強度と入射電磁波の方向平均
(5), (6), (7)式より、逆コンプトン散乱による放射強度を計算しましょう。\(\mu = \cos \theta, \mu_k = \cos \theta_k\)として整理すると
\[\begin{align} \hat{I} (\omega, \mathbf{r}) &= \frac{c R^2 \left( \vert \hat{E}_x \vert^2 + \vert \hat{E}_y \vert^2 + \vert \hat{E}_z \vert^2 \right)}{T'} \notag \\ &= \frac{e^2}{16 \pi^2 c} \frac{\omega^4 \omega_\mathrm{se}^2}{\tilde{\omega}_0^4} \left\{ (\mu_k - \beta_0)^2 (1-\mu \beta_0)^2 \cos^2 \varphi_k + (\mu_k - \beta_0)^2 (\mu - \beta_0)^2 \sin^2 \varphi_k \right. \notag \\ & \qquad \left\{+ \frac{\sin^2 \theta_k}{\gamma^4} \sin^2 \theta + 2(\mu_k - \beta_0) (\mu-\beta_0) \sin \varphi_k \sin \theta \frac{\sin \theta_k}{\gamma^2} \right\} T' \mathrm{sinc}^2 \left[ \{ (1-\beta_0 \mu) \omega -\tilde{\omega}_0\} \frac{T'}{2} \right] \tag{9} \end{align}\]いまは\((\theta_k, \varphi_k)\)方向からの入射電磁波の場合を考えてきました。この角度分布に対して平均を行いましよう。以下では等方的に入射電磁波が飛来することを仮定します。
\[\int_0^{2\pi} \sin^2 \varphi_k d\varphi_k = \int_0^{2\pi} \cos^2 \varphi_k d\varphi_k = \int_0^{2\pi} \frac{1 + \cos 2\varphi_k}{2} d\varphi_k = \pi, \quad \int_0^{2\pi} \sin \varphi_k d\varphi_k = \int_0^{2\pi} \cos \varphi_k d\varphi_k = 0\]より(9)式を\(\varphi_k\)で積分したものは
\[\hat{I}_{\theta_k} (\omega, \mathbf{r}) \equiv \int_0^{2\pi} \hat{I}(\omega, \mathbf{r}) d\varphi_k = \frac{e^2}{16\pi c} \frac{\omega^4 \omega_\mathrm{se}^2}{\tilde{\omega}_0^4} \left\{ (\mu_k -\beta_0)^2 (1-\mu \beta_0)^2 + (\mu_k-\beta_0)^2 (\mu-\beta_0)^2 + \frac{2 (1-\mu_k^2)}{\gamma^4} (1-\mu^2) \right\} T' \mathrm{sinc}^2 \left[ \{ (1-\beta_0 \mu) \omega -\tilde{\omega}_0\} \frac{T'}{2} \right]\]のようになります。続いて\(\theta_k\)の積分です。\(\mu_k = \cos \theta_k\)としているので、その積分範囲は\(\theta_k = 0 \rightarrow \pi\)から\(\mu_k = 1 \rightarrow -1\)になります。よって
\[\hat{I} (\omega, \mathbf{n}) = \frac{1}{4\pi} \int_0^{\pi} \hat{I}_{\theta_k} (\omega, \mathbf{n}) \sin \theta_k d\theta_k = \frac{1}{4\pi} \int_{-1}^1 \hat{I}_{\theta_k} (\omega, \mathbf{n}) d\mu_k\]このとき\(\tilde{\omega}_0 = (1-\beta_0 \mu_k) \omega_0\)より、\(\mu_k = -1 \rightarrow 1\)では\(\tilde{\omega}_0 = 2\omega_0 \rightarrow 0 \ (\beta_0 \sim 1)\)となります。\(\mu_k = \frac{1}{\beta_0} \left( 1- \frac{\tilde{\omega_0}}{\omega_0}\right)\)より\(d\mu_k = - \frac{d\tilde{\omega}_0}{\beta_0 \omega_0}\)なので
\[\hat{I} (\omega, \mathbf{n}) = \frac{e^2}{64 \pi^2 c} \frac{T' \omega^4 \omega_\mathrm{se}^2}{\beta_0 \omega_0}\int_0^{2\omega_0} \frac{1}{\tilde{\omega}_0^4} \left[ \left\{ \frac{1}{\beta_0} \left( 1-\frac{\tilde{\omega}_9}{\omega_0} \right) -\beta_0 \right\}^2 \left\{(1-\mu \beta_0)^2 + (\mu-\beta_0)^2 \right\} + \frac{2}{\gamma^4} \left\{ 1-\frac{1}{\beta_0^2} \left( 1-\frac{\tilde{\omega}_0}{\omega_0} \right)^2\right\}(1-\mu^2) \right] \mathrm{sinc}^2 \left\{ -\frac{T'}{2} \tilde{\omega}_0 + (1-\beta_0 \mu) \omega \frac{T'}{2} \right\} d\tilde{\omega}_0\]となります。さらにsinc関数の積分を行うために、\(X = -\frac{T'}{2} \tilde{\omega}_0\)と置換しましょう。\(\tilde{\omega}_0 = 0 \rightarrow 2\omega_0\)のとき\(X = 0 \rightarrow - \infty \ (T' \gg 1)\)、そして\(d\tilde{\omega}_0 = -\frac{2}{T'} dX\)より
\[\hat{I}(\omega, \mathbf{n}) = \frac{e^2}{64 \pi^2 c} \frac{T' \omega^4 \omega_\mathrm{se}^2}{\beta_0 \omega_0} \int_{-\infty}^0 \frac{1}{\frac{2^4}{T'^4} X^4} \left[ \left\{ \frac{1}{\beta_0} \left( 1+\frac{\frac{2}{T'} X}{\omega_0} \right) -\beta_0 \right\}^2 \left\{(1-\mu \beta_0)^2 + (\mu-\beta_0)^2 \right\} + \frac{2}{\gamma^4} \left\{ 1-\frac{1}{\beta_0^2} \left( 1+\frac{\frac{2}{T'} X}{\omega_0} \right)^2\right\}(1-\mu^2) \right] \mathrm{sinc}^2 \left\{ X + (1-\beta_0 \mu) \omega \frac{T'}{2} \right\} \frac{2}{T'} dX\]今は\(T' \gg 1\)を考えているので、
\[\mathrm{sinc}^2 \left\{ X + (1-\beta_0 \mu) \omega \frac{T'}{2} \right\} = \pi \delta \left( X + (1-\beta_0 \mu) \omega \frac{T'}{2} \right)\]のように、デルタ関数で近似することができます(デルタ関数の前に\(\pi\)が付く理由はこちらをご覧ください)。よって
\[\begin{aligned} \hat{I}(\omega, \mathbf{n}) &= \frac{e^2}{32 \pi c} \frac{\omega^4 \omega_\mathrm{se}^2}{\beta_0 \omega_0} \frac{1}{\frac{2^4}{T'^4} \left\{ -(1-\beta_0 \mu) \omega \frac{T'}{2}\right\}^4} \left[ \left\{ \frac{1}{\beta_0} \left( 1+\frac{\frac{2}{T'} \left\{ -(1-\beta_0 \mu) \omega \frac{T'}{2}\right\}}{\omega_0} \right) -\beta_0 \right\}^2 \left\{(1-\mu \beta_0)^2 + (\mu-\beta_0)^2 \right\} \right. \\ & \qquad \left. + \frac{2}{\gamma^4} \left\{ 1-\frac{1}{\beta_0^2} \left( 1+\frac{\frac{2}{T'} \left\{ -(1-\beta_0 \mu) \omega \frac{T'}{2}\right\}}{\omega_0} \right)^2\right\}(1-\mu^2) \right] \\ &= \frac{e^2}{32 \pi c} \frac{\omega_\mathrm{se}^2}{\beta_0 \omega_0} \frac{1}{(1-\beta_0 \mu)^4} \left[ \left\{ \frac{1}{\beta_0} \left( 1- (1-\beta_0 \mu) \frac{\omega}{\omega_0} \right) -\beta_0 \right\}^2 \left\{(1-\mu \beta_0)^2 + (\mu-\beta_0)^2 \right\} \right. \\ & \qquad \left. + \frac{2}{\gamma^4} \left\{ 1-\frac{1}{\beta_0^2} \left( 1-(1-\beta_0 \mu) \frac{\omega}{\omega_0} \right)^2\right\}(1-\mu^2) \right] \end{aligned}\]上式の\([ \cdots ]\)の部分を整理しましょう。\(\gamma^2 = \frac{1}{1-\beta_0^2}\)より
\[\begin{aligned} [ \cdots ] &= \frac{1}{\beta_0^2} \left\{ \frac{1}{\gamma^2} -(1-\beta_0 \mu) \frac{\omega}{\omega_0} \right\}^2 + \frac{2}{\beta_0^2 \gamma^4} \left\{ -\frac{1}{\gamma^2} + 2(1-\beta_0 \mu) \frac{\omega}{\omega_0} - (1-\beta_0 \mu)^2 \frac{\omega^2}{\omega_0^2}\right\} \\ &= \frac{(1-\beta_0 \mu)^2}{\beta_0^2} \left\{ \frac{1}{\gamma^4} -\frac{2}{\gamma^2} (1-\beta_0 \mu) \frac{\omega}{\omega_0} + (1-\beta_0\mu)^2 \frac{\omega^2}{\omega_0^2} \right\} + \frac{(\mu -\beta_0)^2}{\beta_0^2} \left\{ \frac{1}{\gamma^4} -\frac{2}{\gamma^2} (1-\beta_0 \mu) \frac{\omega}{\omega_0} + (1-\beta_0 \mu)^2 \frac{\omega^2}{\omega_0^2} \right\} \\ & \qquad + \frac{2}{\gamma^4} \frac{1-\mu^2}{\beta_0^2} \left\{ -\frac{1}{\gamma^2} + 2(1-\beta_0 \mu) \frac{\omega}{\omega_0} - (1-\beta_0 \mu)^2 \frac{\omega^2}{\omega_0^2} \right\} \end{aligned}\]ここで
\[\begin{aligned} 1-\mu^2 &= (1-\mu)(1+\mu) = \frac{1}{\beta_0^2} (\beta_0 - \beta_0 \mu) (\beta_0 + \beta_0 \mu) = \frac{1}{\beta_0^2} \{ \beta_0 + (1 - \beta_0 \mu) -1 \} \{ \beta_0 - (1 - \beta_0 \mu) +1\} \\ &= \frac{1}{\beta_0^2} \{ \beta_0^2 + 2(1-\beta_0 \mu) - (1-\beta_0 \mu)^2 - 1\} = \frac{1}{\beta_0^2} \left\{ -\frac{1}{\gamma^2} + 2(1-\beta_0 \mu) - (1-\beta_0 \mu)^2 \right\} \end{aligned}\] \[\begin{aligned} (\mu - \beta_0)^2 &= \mu^2 - 2\beta_0 \mu + \beta_0^2 = \frac{1}{\beta_0^2} (\beta_0^2 \mu^2 - 2\beta_0^3 \mu + \beta_0^4) \\ = \frac{1}{\beta_0^2} \{ (1-\beta_0 \mu)^2 -1 + 2\beta_0 \mu- 2 \beta_0^3 \mu + \beta_0^4\} &= \frac{1}{\beta_0^2} \{ (1-\beta_0 \mu)^2 -1 -2 (1-\beta_0^2) (1-\mu \beta_0) + 2 -2 \beta_0^2 + \beta_0^4\} = \frac{1}{\beta_0^2} \left\{ (1-\beta_0 \mu)^2 -\frac{2}{\gamma^2} (1-\mu \beta_0) + 1 -2 \beta_0^2 + \beta_0^4 \right\} &= \frac{1}{\beta_0^2} \left\{ (1-\beta_0 \mu)^2 -\frac{2}{\gamma^2} (1-\mu \beta_0) + \frac{1}{\gamma^4} \right\} \end{aligned}\]を組合わせることで
\[\begin{aligned} \hat{I}(\omega, \mathbf{n}) &= \frac{e^2}{32\pi c} \frac{\omega_\mathrm{se}^2}{\beta_0 \omega_0} \left[ \frac{1}{\beta_0^2} \left\{ \frac{1}{\gamma^4 (1-\beta_0 \mu)^2} - \frac{2}{\gamma^2 (1-\beta_0 \mu)} \frac{\omega}{\omega_0} + \frac{\omega^2}{\omega_0^2}\right\} + \frac{1}{\beta_0^4} \left\{ 1-\frac{2}{\gamma^2 (1-\beta_0 \mu)} + \frac{1}{\gamma^4 (1-\beta_0 \mu)^2} \right\} \left\{ \frac{1}{\gamma^4 (1-\beta_0 \mu)^2} - \frac{2}{\gamma^2 (1-\beta_0 \mu)} \frac{\omega}{\omega_0} + \frac{\omega^2}{\omega_0^2} \right\} \right. \\ &\qquad \left. + \frac{2}{\gamma^4 \beta_0^4} \left\{ -\frac{1}{\gamma^2 (1-\beta_0 \mu)^2} -\frac{2}{1-\beta_0 \mu} - 1\right\} \left\{ -\frac{1}{\gamma^2 (1-\beta_0 \mu)^2} \frac{2}{1-\beta_0 \mu} \frac{\omega}{\omega_0} -\frac{\omega^2}{\omega_0^2}\right\}\right] \end{aligned}\]ここまで式変形したところで、(8)式と逆コンプトン散乱による光子エネルギー変化が\(\gamma^2\)程度であることより
\[1-\beta_0 \mu = \frac{\omega_0}{\omega} (1-\beta_0 \mu_k) \simeq \mathcal{O}(1/\gamma^2)\]であることから、例えば\(1/(\gamma^4 (1-\beta_0 \mu)^2) \simeq \mathcal{O}(1), \omega/( \omega_0 \gamma^2 (1-\beta_0 \mu)) \simeq \mathcal{O}(\gamma^2), \omega^2 / \omega_0^2 \simeq \mathcal{O}(\gamma^4)\)のようになります。\(\gamma \gg 1\)より、\(\mathcal{O}(\gamma^4)\)の項だけを取り出しましょう。\(\beta_0 \sim 1\)より
\[\hat{I}(\omega, \mathbf{n}) = \frac{e^2}{32\pi c} \frac{\omega_\mathrm{se}^2}{\omega_0} \left[ \frac{\omega^2}{\omega_0^2} + \frac{\omega^2}{\omega_0^2} \left\{ 1-\frac{2}{\gamma^2 (1-\beta_0 \mu)} + \frac{1}{\gamma^4 (1-\beta_0 \mu)^2}\right\}\right]\]最後に\(x \equiv 1-\beta_0 \mu\)とすれば
\[\hat{I}(\omega, \mathbf{n}) = \frac{e^2}{32\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \left( 2-\frac{2}{\gamma^2}\frac{1}{x} + \frac{1}{\gamma^4} \frac{1}{x^2}\right) \tag{10}\]を得ます。
電子の方向分布に対する平均
次に電子の方向分布について平均していきましょう。ここでは電子の分布は等方的であるとします。平均をするには視線方向\(\mathbf{n}\)を\(z\)方向にとり\(\boldsymbol{\beta}\)の方向について平均すれば良いですが、ここまでの計算では\(\boldsymbol{\beta}_0\)を\(z\)方向にとり、\(\mathbf{n}\)を\(yz\)平面内としていました。しかし、(10)式を見ると方向分布について平均した結果は\(\boldsymbol{\beta}_0, \mathbf{n}\)以外に特別な方向は存在せず、また\(\hat{I}(\omega, \mathbf{n})\)は\(\varphi\)に依存しません。よって\(\hat{I}(\omega, \mathbf{n})\)の\(\mathbf{n}\)を\(z\)軸としたときの結果とみなしても差し支えありません。以上の議論から、電子の速度の方向分布についての平均は\(\theta, \varphi\)についての平均を計算することで実行されます。以下では\(\theta\)の代わりに\(\mu\)を積分変数として扱います。(8)式より
\[\mu = \frac{1}{\beta_0} \left( 1-\frac{\omega}{\omega_0} (1-\beta_0 \mu_k)\right)\]となります。積分変数である\(\mu = \cos \theta\)は\(-1 \leq \mu \leq 1\)をとりそうですが、今回の場合は逆コンプトン散乱により\(\omega > \omega_0\)です。よって\(\mu_k = -1\)のとき
\[\mu = \frac{1}{\beta_0} \left( 1-\frac{\omega_0}{\omega} (1+\beta_0)\right) \underbrace{\simeq}_{\beta_0 \sim 1} 1-\frac{2 \omega_0}{\omega} \equiv \mu_m\]です。\(\mu_k = 1\)のときは
\[\mu = \frac{1}{\beta_0} \left(1-\frac{\omega_0}{\omega} (1-\beta_0) \right) \simeq \frac{1}{\beta_0} \simeq 1\]となります。よって\(\mu_m < \mu < 1\)が積分範囲となります。以上を用いて積分を実行しましょう。
\[\langle \hat{I} (\omega)\rangle = \frac{1}{4\pi} \int_{4\pi} \hat{I}(\omega, \mathbf{n}) d\Omega = \frac{1}{4\pi} \int_{\mu_m}^1 d\mu \int_0^{2\pi} d\varphi \frac{e^2}{32\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \left( 2 - \frac{2}{\gamma^2} \frac{1}{x} + \frac{1}{\gamma^4} \frac{1}{x^2} \right)\]\(x = 1-\beta_0 \mu\)より\(dx = -\beta_0 d\mu\)、そしてその積分範囲は
\[x_\mathrm{min} = 1-\beta_0 \mu_m = 1- \beta_0 + \frac{2\omega_0}{\omega} \beta_0 \underbrace{\simeq}_{\beta \sim 1} \frac{2\omega_0}{\omega}\] \[x_\mathrm{max} = 1-\beta_0 \simeq \frac{1}{2\gamma^2}\]より
\[\begin{aligned} \langle \hat{I} (\omega)\rangle &= \frac{e^2}{64\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \int_{x_\mathrm{min}}^{x_\mathrm{max}} \left( 2 - \frac{2}{\gamma^2} \frac{1}{x} + \frac{1}{\gamma^4} \frac{1}{x^2} \right) \left( -\frac{dx}{\beta_0} \right) \\ &\underbrace{=}_{\beta_0 \sim 1} - \frac{e^2}{64\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \left[ 2x - \frac{2}{\gamma^2} \ln x - \frac{1}{\gamma^4} \frac{1}{x} \right]_{x_\mathrm{min}}^{x_\mathrm{max}} \\ &= - \frac{e^2}{64\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \left\{ 2(x_\mathrm{max} - x_\mathrm{min}) - \frac{2}{\gamma^2} \ln \frac{x_\mathrm{max}}{x_\mathrm{min}} - \frac{1}{\gamma^4} \left(\frac{1}{x_\mathrm{max}} - \frac{1}{x_\mathrm{min}} \right) \right\} \\ &= - \frac{e^2}{64\pi c} \frac{\omega^2 \omega_\mathrm{se}^2}{\omega_0^3} \left\{ 2 \left( \frac{1}{2\gamma^2} - \frac{2\omega_0}{\omega} \right) - \frac{2}{\gamma^2} \ln \frac{\omega}{4\gamma^2 \omega_0} - \frac{1}{\gamma^4} \left(2\gamma^2 - \frac{\omega}{2 \omega_0}\right) \right\} \end{aligned}\]ここで\(\hat{\omega} \equiv \frac{\omega}{4\gamma^2 \omega_0}\)のように定義すると
\[\langle \hat{I} (\omega) \rangle = \frac{e^2}{16\pi c} \frac{\omega \omega_\mathrm{se}^2}{\omega_0^2} ( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 )\]のように整理されます。ここで\(\hat{\omega}\)は、\(\omega_0\)の入射光子が逆コンプトン散乱を受けたときに到達しうる最大の周波数で規格化された周波数です。\(\omega_\mathrm{se} = \frac{eB}{\gamma m_e c}\)であることを思い出すと
\[\langle \hat{I}(\omega)\rangle = \frac{e^2}{16\pi c} \frac{\omega}{\omega_0^2} \frac{e^2 B^2}{\gamma^2 m_e^2 c^2} ( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 )\]ここに電磁場のポインティングベクトルの時間平均\(\langle S \rangle = \frac{c B^2}{8\pi}\)と、古典電子半径\(r_0 = \frac{e^2}{m_e c^2}\)を用いることで
\[\langle \hat{I} (\omega) \rangle = 2 r_0^2 \frac{\langle S(\omega_0)\rangle}{\omega_0} \hat{\omega}( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 ) \tag{11}\]この結果から、ローレンツ因子が\(\gamma\)の等方分布した電子群が、同じく等方分布をした周波数\(\omega_0\)の電磁波を逆コンプトン散乱したとき、その散乱波の周波数分布は
\[f(\hat{\omega}) = \hat{\omega}( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 ) \tag{12}\]で与えられることを示しています。(12)式を図示したものを下図に示します。

\(\hat{\omega} = \frac{\omega}{4\gamma^2 \omega_0}= 0\)、すなわち逆コンプトン散乱後に\(\omega=0\)であるような放射はないことがわかります。逆コンプトン散乱により\(\omega_0\)からエネルギーを獲得していることが考えられるため、\(\omega=0\)にはならないという直感に一致します。 同様に\(\hat{\omega} = 1\)、すなわち電子との正面衝突により最大エネルギーを獲得するような放射もないことがわかります。最大エネルギーの獲得は滅多に起こることではないという、こちらも直感的に理解できます。
電子のエネルギー分布がべき乗分布のとき
次に電子のエネルギー分布が
\[N(\gamma) d\gamma = N_0 \left( \frac{\gamma}{\gamma_0}\right)^{-p} \frac{d\gamma}{\gamma_0} \quad (\gamma_1 < \gamma< \gamma_2) \tag{13}\]で与えられるとき、この電子群からの逆コンプトン散乱による放射スペクトルを計算してみましょう。このために、\(\gamma\)による積分を\(\hat{\omega}\)に変換します。今、\(\omega\)を固定して「この\(\omega\)のときの放射強度」のような形で求めたいので、\(\gamma\)には下限値 \(\gamma_\mathrm{min} = \left( \frac{\omega}{4\omega_0}\right)^{1/2}\)が存在します。よって積分の下限は(13)式の\(\gamma_1\)と\(\gamma_m\)のうち、より大きな方、すなわち\(\gamma_\mathrm{min} = \max (\gamma_1, \gamma_m)\)となります。 \(\gamma = \gamma_\mathrm{min} \rightarrow \gamma_2\)のときの\(\hat{\omega}\)について考えてみましょう。\(\gamma_2 \gg \gamma_\mathrm{min}\)のとき、\(\hat{\omega} = \frac{\omega}{4\gamma^2 \omega_0} \rightarrow 0\)としても差し支えないでしょう。 逆に\(\gamma = \gamma_\mathrm{min} = \left( \frac{\omega}{4\omega_0}\right)^{1/2}\)のとき、\(\hat{\omega} = 1\)となります。よって
\[\gamma = \left( \frac{\omega}{4\omega_0}\right)^{1/2} \hat{\omega}^{-1/2}\]と
\[d\gamma = - \frac{1}{4} \left( \frac{\omega}{4\omega_0}\right)^{1/2} \hat{\omega}^{-3/2} d\hat{\omega}\]より、積分を実行しましょう。
\[\begin{aligned} \frac{dW (\nu, \nu_0)}{dt d\Omega d\omega} &= 2 r_0^2 \frac{\langle S(\omega_0)\rangle}{\omega_0} \int_{1}^{0} f(\hat{\omega}) N_0 \left( \frac{\omega}{4\omega_0} \right)^{-p/2} \hat{\omega}^{p/2} \gamma_0^p \frac{- \frac{1}{4} \left( \frac{\omega}{4\omega_0}\right)^{1/2} \hat{\omega}^{-3/2}}{\gamma_0} d\hat{\omega} \\ &= 2^{p-1} r_0^2 \langle S(\omega_0)\rangle N_0 \left( \frac{\omega_0}{\omega} \right)^{\frac{p-1}{2}} \frac{1}{\omega_0} \gamma_0^{p-1} \int_0^1 f(\hat{\omega}) \hat{\omega}^{\frac{p-3}{2}} d\hat{\omega} \end{aligned}\]最後の積分部分の計算を実行します。
\[\begin{aligned} \int_0^1 f(\hat{\omega}) \hat{\omega}^{\frac{p-3}{2}} d\hat{\omega} &= \int_0^1 \hat{\omega}^{\frac{p-1}{2}} ( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 ) d\hat{\omega} = \int_0^1 \hat{\omega}^{\frac{p-1}{2}} ( 1 + \hat{\omega} + 2 \hat{\omega} \ln \hat{\omega} - 2 \hat{\omega}^2 ) d\hat{\omega} \\ &= \left[ \frac{2}{p+1} \hat{\omega}^{\frac{p+1}{2}} + \frac{2}{p+3} \hat{\omega}^{\frac{p+3}{2}} - \frac{4}{p+5} \hat{\omega}^{\frac{p+5}{2}} \right]_0^1 + \left[ \frac{4}{p+3} \hat{\omega}^{\frac{p+3}{2}} \ln \hat{\omega}\right] - \int_0^1 \frac{4}{p+3} \int_0^1 \hat{\omega}^{\frac{p+1}{2}} d\hat{\omega} \\ &= \frac{2}{p+1} + \frac{2}{p+3} - \frac{4}{p+5} - \frac{4}{p+3} \frac{2}{p+3} = 4\frac{p^2-4p+11}{(p+1)(p+3)^2 (p+5)} \end{aligned}\]以上より
\[\frac{dW (\nu, \nu_0)}{dt d\Omega d\omega} = 2^{p+1} r_0^2 \langle S(\omega_0)\rangle N_0 \left( \frac{\omega_0}{\omega} \right)^{\frac{p-1}{2}} \frac{1}{\omega_0} \gamma_0^{p-1} \frac{p^2-4p+11}{(p+1)(p+3)^2 (p+5)}\]ここで\(\omega = 2\pi \nu\)のように、角振動数から振動数への変換を行うと
\[\begin{align} &\frac{1}{2\pi} \frac{dW (\nu, \nu_0)}{dt d\Omega d\nu} = 2^{p+1} r_0^2 \langle S(\omega_0)\rangle N_0 \left( \frac{\nu_0}{\nu} \right)^{\frac{p-1}{2}} \frac{1}{2\pi \nu_0} \gamma_0^{p-1} \frac{p^2-4p+11}{(p+1)(p+3)^2 (p+5)} \notag \\ &\Longrightarrow \ \frac{dW(\nu, \nu_0)}{dt d\Omega d\nu} = \frac{1}{4} r_0^2 \langle S(\nu_0) \rangle N_0 \gamma_0^{p-1} \nu_0^{\frac{p-3}{2}} F(p) \nu^{-\frac{p-1}{2}} \quad \left( F(p) \equiv 2^{p+3} \frac{p^2-4p+11}{(p+1)(p+3)^2 (p+5)} \right) \tag{14} \end{align}\]
入射波が黒体放射のとき
ここに、入射波のスペクトルを入力することで、その入射波が逆コンプトン散乱を受けたことで発生するスペクトルが求まります。ここでは入射波として、CMBのような温度\(T\)の黒体放射を考えましょう。このとき
\[\langle S(\nu_0)\rangle = 4\pi \frac{2h\nu_0^3}{c^2} \frac{1}{e^{\frac{h\nu_0}{k_B T}} - 1} d\nu_0\]です。右辺の\(4\pi\)はプランク関数が単位立体角あたりの放射強度であるのに対し、左辺のポインティングベクトルは立体角積分した結果であることからくるものです。散乱波の周波数が\(\nu\)となるために、入射波の周波数には下限が存在します。よって\(\nu_0 > \frac{\nu}{4\gamma_1}\)の条件を満たしていることが必要条件となります。しかし、以下では\(\gamma_1\)が十分大きいとして、\(\frac{\nu}{4\gamma_1^2} \ll k_B T\)となる\(\nu\)の範囲を扱うとします。すなわち\(\nu_0\)の積分範囲は\([0, \infty]\)とします。以上から、単位周波数・単位時間・単位立体角あたりの逆コンプトン散乱の放射強度スペクトルを計算しましょう。
\[\begin{aligned} \frac{dW}{d\nu dt d\Omega} &= \int_0^\infty d\nu_0 \frac{1}{4} r_0^2 4\pi \frac{2h\nu_0^3}{c^2} \frac{1}{\exp \left( \frac{h\nu}{k_B T}\right) - 1} N_0 \gamma_0^{p-1} \nu_0^{\frac{p-3}{2}} F(p) \nu^{-\frac{p-1}{2}} \\ &= \frac{2h r_o^2 \pi}{c^2} N_0 \gamma_0^{p-1} F(p) \nu^{-\frac{p-1}{2}} \int_0^\infty \frac{\nu_0^{\frac{p+3}{2}}}{e^{\frac{h\nu_0}{k_B T}} - 1} d\nu_0 \\ &\underbrace{=}_{x = \frac{h\nu_0}{k_B T}} \frac{2h r_o^2 \pi}{c^2} N_0 \gamma_0^{p-1} F(p) \nu^{-\frac{p-1}{2}} \left( \frac{k_B T}{h}\right)^{\frac{p+5}{2}} \int_0^\infty \frac{x^{\frac{p+3}{2}}}{e^x-1} dx \end{aligned}\]ゼータ関数より
\[\int_0^\infty \frac{x^{\frac{p+3}{2}}}{e^x-1} dx = \zeta \left( \frac{p+5}{2} \right) \Gamma \left( \frac{p+5}{2} \right)\]のように計算されるので
\[\frac{dW}{d\nu dt d\Omega} = \frac{2h r_o^2 \pi}{c^2} N_0 \gamma_0^{p-1} F(p) \left( \frac{k_B T}{h}\right)^{\frac{p+5}{2}} \zeta \left( \frac{p+5}{2} \right) \Gamma \left( \frac{p+5}{2} \right) \nu^{-\frac{p-1}{2}} \tag{15} \propto \nu^{-\frac{p-1}{2}}\]のようになります。\(\nu^{-\frac{p-1}{2}}\)のようなスペクトルの振る舞いは、シンクロトロン放射のスペクトルのときにも出現しました。電子のエネルギー分布としてべき乗分布を仮定すると、常にこのような分布が出現するのかもしれません。
余談: 別解法
これまでは相対論的な電子が入射電磁波により運動を始めたときに放射する電磁波を計算する、という観点から導出を行ってきました。しかし(12)式の導出には別の手法が存在します。エネルギー空間での光子数分布を\(f(\epsilon)\)(運動量空間ならば\(f(\mathbf{p})\))のように考え、そこから単位時間・単位立体角あたりに散乱される光子の数\(\frac{dN}{dt d\Omega}\)から出発するという、光子の散乱を厳密に取り扱った方法です。この方法については(また体力のあるときに)別記事にて解説したいと思います。
参考文献
- [1] Rybicki & Lightman, 1986, “Radiative Processes in Astrophysics”
- [2] Geoff Bicknell’s Home Page, Lecture Notes and Exercises on High Energy Astrophysics
- [3] Blumenthal & Gould, 1970, “Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Travering Dilute Gases”
- [4] 茅根裕司, レポート倉庫, コンプトン散乱