Table of contents
パルサー磁気圏
ここでは、パルサー磁気圏について勉強したものをメモしていきます。 そこまで詳細には触れず、簡単化されたモデルを見ていきましょう。
真空モデル
ここでは、自転する中性子星が双極子磁場を持っているとします。 ただしこの双極子磁場の軸は、回転軸と一致しているものとします。
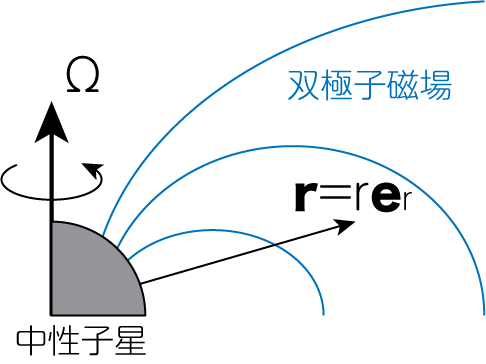
すると中性子星外部の磁場は、以下のように書くことができます。
\[\mathbf{B}^\mathrm{(out)} = B_p R^3 \left( \frac{\cos \theta}{r^3} \mathbf{e}_r + \frac{\sin \theta}{2r^3} \mathbf{e}_\theta \right) \tag{1}\]ここで\(R\)は中性子星の半径、\(B_p\)は双極子磁場の大きさを表す定数です。 中性子星内部は電気伝導度がとても高く、完全導体のように扱うことができるとします。 すると、導体内は電流が存在しないため、オームの法則から
\[\mathbf{E}^\mathrm{(in)} + (\boldsymbol{\Omega} \times \mathbf{r}) \times \frac{\mathbf{B}^\mathrm{(in)}}{c} = \mathbf{0} \tag{2}\]を満たす必要があります。 さらに中性子星表面にも電流は流れておらず、中性子星およびその周囲の空間は定常状態に落ち着いているとしましょう。 すると、\(\mathbf{B}\)の成分は連続でなければならないことがわかります。 ここから、中性子星表面から少しだけ内側の磁場が
\[\mathbf{B}^\mathrm{(in)} = B_p \left( \cos \theta \mathbf{e}_r + \frac{\sin \theta}{2} \mathbf{e}_\theta \right) \tag{3}\]とわかります。 (3)式を(2)式に入れることで、表面から少し内側の電場は
\[\begin{align} \mathbf{E}^\mathrm{(in)} &= - (\boldsymbol{\Omega} \times \mathbf{R}) \times \frac{\mathbf{B}^\mathrm{(in)}}{c} = - R \Omega \sin \theta \mathbf{e}_\varphi \times \frac{B_p}{c} \left( \cos \theta \mathbf{e}_r + \frac{\sin \theta}{2} \mathbf{e}_\theta \right) \notag \\ &= - \frac{R \Omega B_p \sin \theta}{c} \left( \cos \theta \mathbf{e}_\theta - \frac{\sin \theta}{2} \mathbf{e}_r \right) \tag{4} \end{align}\]のように計算されます。 完全導体表面では、電場\(\mathbf{E}\)の接線方向\(E_\theta\)が連続でなければなりません。 すると(4)式から
\[E_\theta^\mathrm{(out)} = - \frac{R \Omega B_p}{c} \sin \theta \cos \theta = - \frac{R \Omega B_p}{2c} \frac{\partial}{\partial \theta} \sin^2 \theta\]です。 ここで、ルジャンドル多項式 \(P_2 (\cos \theta) = \frac{1}{2} (3\cos^2 \theta - 1)\)より
\[E_\theta^\mathrm{(out)} = \frac{R \Omega B_p}{3c} \frac{\partial }{\partial \theta} \left( P_2 (\cos \theta) - 1 \right) = \frac{R \Omega B_p}{3c} \frac{\partial P_2 (\cos \theta)}{\partial \theta} \tag{5}\]のように整理されます。 中性子星の外側は真空であるとすると、電場およびその静電ポテンシャルは
\[\mathbf{E}^\mathrm{(out)} = - \nabla \phi, \quad \nabla^2 \phi = 0 \tag{6}\]を満たします。 \(r = R\)での境界条件(5)式を満たすような静電ポテンシャルを計算しましょう。
\[- \frac{1}{R} \frac{\partial \phi}{\partial \theta} = \frac{R \Omega B_p}{3c} \frac{\partial P_2 (\cos \theta)}{\partial \theta} \ \Longrightarrow \ \phi (R, \theta) = - \frac{R^2 \Omega B_p}{3c} P_2 (\cos \theta)\]のようになります。 電気双極子の静電ポテンシャルが\(r^{-3}\)で減衰することを既知の事実として用いると
\[\phi (r, \theta) = - \frac{B_p \Omega}{3c} \frac{R^5}{r^3} P_2 (\cos \theta) \tag{7}\]のように、中性子星外部の静電ポテンシャルを求めることができました。 そして、(6), (7)式から、中性子星外部での電場の成分がそれぞれ
\[E_r^\mathrm{(out)} = - \frac{\partial \phi}{\partial r} = \frac{B_p \Omega}{2c} \frac{R^5}{r^4} (3\cos^2 \theta - 1) \tag{8}\] \[E_\theta^\mathrm{(out)} = - \frac{1}{r} \frac{\partial \phi}{\partial \theta} = \frac{B_p \Omega}{c} \frac{R^5}{r^4} \sin \theta \cos \theta \tag{9}\]パルサー磁気圏: 重力と静電気力はどちらが支配的か?
中性子星内部においては
\[\mathbf{E}^\mathrm{(in)} \cdot \mathbf{B}^\mathrm{(in)} \underbrace{=}_{(2)} - \left\{ (\boldsymbol{\Omega} \times \mathbf{r}) \times \frac{\mathbf{B}^\mathrm{(in)}}{c} \right\} \cdot \mathbf{B}^\mathrm{(in)} = 0 \tag{10}\]のように、電場と磁場が直交していることがわかります。 一方、中性子星外部では、(1), (8), (9)式より
\[\begin{align} \mathbf{E}^\mathrm{(out)} \cdot \mathbf{B}^\mathrm{(out)} &= \frac{R B_p^2 \Omega}{2c} \left( \frac{R}{r} \right)^7 (3 \cos^2 \theta - 1) \cos \theta + \frac{R B_p^2 \Omega}{2c} \left( \frac{R}{r} \right)^7 \sin^2 \theta \cos \theta \notag \\ &= \frac{R B_p^2 \Omega}{c} \left( \frac{R}{r} \right)^7 \cos^3 \theta \tag{11} \end{align}\]のように、磁場に沿った方向の電場が存在することがわかります。 \(r = R\)、すなわち中性子星表面において、この磁場に沿った方向の電場の大きさは大雑把に
\[E_\parallel \approx \frac{R\Omega}{c} B_p \approx 2\pi \frac{R}{c} \frac{\Omega}{2\pi} B_p \approx 2 \times 10^8 P^{-1} B_{12} \ [\mathrm{V/cm}] \tag{12}\]のように求まります。 ここで\(R \sim 10 \mathrm{km}, B_{12} = \frac{B_p}{10^{12} \mathrm{G}}\)のように、中性子星の典型的な値を用いました。 この電場が中性子星表面に存在する陽子に与える力と、重力を比較してみましょう。
\[\frac{電場による静電気力}{重力} \approx \frac{\frac{eR\Omega B_p}{c}}{\frac{GMm_p}{R^2}} \approx 10^9 P^{-1} B_{12} \gg 1 \tag{13}\]以上から、中性子星表面に存在する荷電粒子は表面から離れていき、中性子星周囲にプラズマで覆われた領域を作ることがわかります。 これを中性子星の磁気圏 (magnetosphere)と呼びます。 ここまでは、自転する中性子星外部が真空であると議論してきました。 しかし、この解は表面に少しでもプラズマが存在する場合、プラズマが表面から離れるため、外部が真空であるという仮定が成り立たなくなる(不安定である)ことがわかります。
Goldreich & Julian (1969)のモデル
この不安定さを解決するために、Goldreich & Julian (1969)では、中性子星の外側領域がプラズマで覆われているモデルを提案しました。 ここではこのモデルについて見ていきましょう。
先程は中性子星内部が導体であるとしましたが、プラズマで満たされた磁気圏も電気伝導度が高いとします。 すなわち
磁気圏における電荷密度\(\rho_e = e (n_+ - n_-)\)は、ガウスの法則から以下のようになります。
\[4\pi \rho_e = \nabla \cdot \mathbf{E}^\mathrm{(out)} \underbrace{=}_{(14)} - \nabla \cdot \left\{ (\boldsymbol{\Omega} \times \mathbf{r}) \times \frac{\mathbf{B}^\mathrm{(out)}}{c} \right\} \tag{15}\]ここで、外積をレビチビタテンソル\(\epsilon_{ijk}\)を用いて表現し、ベクトル計算を進めていきましょう。 このとき、中性子星は剛体回転しているとして\(\frac{\partial \Omega_i}{\partial r_j} = 0\)とすると
\[\begin{align} \nabla \cdot \{ (\boldsymbol{\Omega} \times \mathbf{r}) \times \mathbf{B}^\mathrm{(out)} \} &= \partial_i \{ (\boldsymbol{\Omega} \times \mathbf{r}) \times \mathbf{B}^\mathrm{(out)} \}_i = \partial_i \epsilon_{ijk} (\boldsymbol{\Omega} \times \mathbf{r})_j B^\mathrm{(out)}_k = \partial_i \epsilon_{ijk} \epsilon_{j\ell m} \Omega_\ell r_m B^\mathrm{(out)}_k \notag \\ &= \epsilon_{ijk} \epsilon_{j\ell m} \Omega_\ell \partial_i (r_m B^\mathrm{(out)}_k) \notag \\ &= \epsilon_{ijk} \epsilon_{j\ell m} \Omega_\ell \{ \delta_{im} B^\mathrm{(out)}_k + r_m (\partial_i B^\mathrm{(out)}_k) \} \notag \\ &= \epsilon_{ijk} \epsilon_{j \ell i} \Omega_\ell B^\mathrm{(out)}_k + \epsilon_{ijk} \epsilon_{j\ell m} \Omega_\ell r_m (\partial_i B^\mathrm{(out)}_k) \notag \\ &= \epsilon_{ijk} \epsilon_{i j \ell } \Omega_\ell B^\mathrm{(out)}_k + \epsilon_{j\ell m} \Omega_\ell r_m \epsilon_{jki} (\partial_i B^\mathrm{(out)}_k) \notag \\ &= (\delta_{jj} \delta_{k \ell} - \delta_{j \ell} \delta (k j)) \Omega_\ell B^\mathrm{(out)}_k - \epsilon_{j\ell m} \Omega_\ell r_m \epsilon_{jik} (\partial_i B^\mathrm{(out)}_k) \notag \\ &= (3 \delta_{k \ell} - \delta_{\ell k}) \Omega_\ell B^\mathrm{(out)}_k - (\boldsymbol{\Omega} \times \mathbf{r})_j (\nabla \times \mathbf{B}^\mathrm{(out)})_j \notag \\ &= 2 \boldsymbol{\Omega} \cdot \mathbf{B}^\mathrm{(out)} - (\boldsymbol{\Omega} \times \mathbf{r}) \cdot (\nabla \times \mathbf{B}^\mathrm{(out)}) \notag \end{align}\]のように整理されます。 これより、(15)式は
\[4\pi \rho_e = - \frac{2}{c} \boldsymbol{\Omega} \cdot \mathbf{B}^\mathrm{(out)} + \frac{1}{c} (\boldsymbol{\Omega} \times \mathbf{r}) \cdot (\nabla \times \mathbf{B}^\mathrm{(out)}) \tag{16}\]のようになります。 さらに、磁気圏は定常状態に落ち着いていると仮定し、電流が流れていないとしましょう。 するとマクスウェル方程式から\(\nabla \times \mathbf{B}^\mathrm{(out)} = \mathbf{0}\)より
\[\rho_e = - \frac{1}{2\pi c} \boldsymbol{\Omega} \cdot \mathbf{B}^\mathrm{(out)} \tag{17}\]を得ます。 このことから、磁気圏の電子数密度\(n_e\)は大雑把に
\[n_e = - \frac{\rho_e}{e} \approx \frac{B_z \Omega}{2\pi c e} = 7 \times 10^{-2} P^{-1} B_z \ [\mathrm{esu/cm^3}] \tag{18}\]のようになります。 ここで\(\boldsymbol{\Omega} = \Omega \mathbf{e}_z\)であり、\(\mathbf{B}^\mathrm{(out)} \cdot \boldsymbol{\Omega} = B_z \Omega\)のようにしました。 この数密度\(n_\mathrm{GJ} = \vert \frac{B_z \Omega}{2\pi c e} \vert\)を、ゴールドライヒ・ジュリアンの数密度 (Goldreich-Julian density)と呼びます。
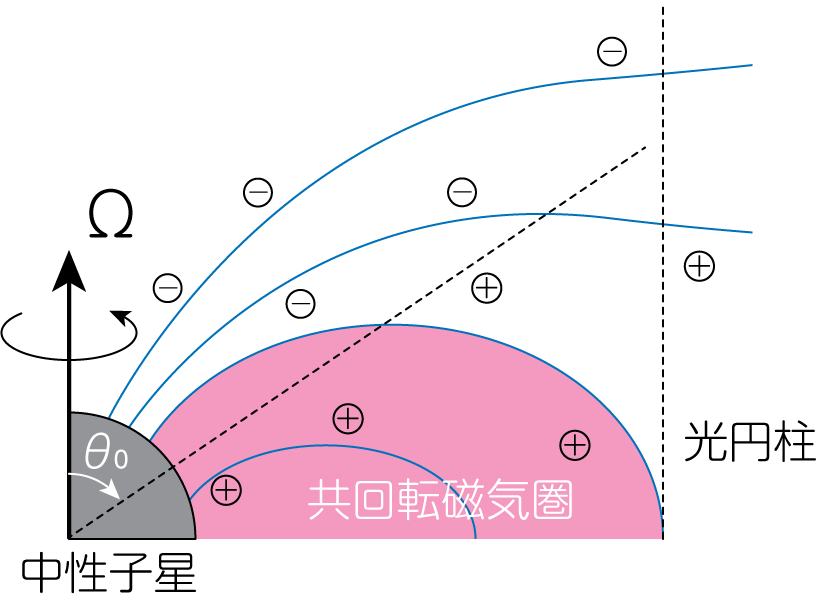
ここでさらに、中性子星磁気圏の磁場が双極子磁場、すなわち(1)式のように表現されるとしましょう。 すると(17)式は
となります。 このことから、角度\(\theta\)によって電荷の正負が異なることがわかります。 実際に(19)式から正負が反転する角度を求めてみましょう。 すると
\[\cos^2 \theta_0 - \frac{\sin^2 \theta_0}{2} = 0 \ \Longrightarrow \ \tan \theta_0 = \sqrt{2} \tag{20}\]となります。 \(\theta_0\)は50度程度であり、この角度より小さい(中性子星の極域)側ではマイナスの電荷、この角度より大きい(中性子星の赤道)側ではプラスの電荷が存在していることがわかります。
双極子磁場(1)式と(14)式から、磁気圏の電場は
\[\mathbf{E}^\mathrm{(out)} = - \Omega r \sin \theta \mathbf{e}_\varphi \times B_p R^3 \left( \frac{\cos \theta}{r^3} \mathbf{e}_r + \frac{\sin \theta}{2r^3} \mathbf{e}_\theta \right) = - \frac{R^3 \Omega B_p}{c r^2} \sin \theta \left( \cos \theta \mathbf{e}_\theta - \frac{1}{2} \sin \theta \mathbf{e}_r \right) \tag{21}\]のように計算されます。 この計算からもわかるように、\(\mathbf{E}^\mathrm{(out)} \cdot \mathbf{B}^\mathrm{(out)} = 0\)です。 さらにこの電場を作る静電ポテンシャルを\(\Phi\)としましょう。 すると
\[\mathbf{E}^\mathrm{(out)} = -\nabla \Phi (r, \theta) \ \Longrightarrow \ \Phi (R, \theta) = \frac{R^2 \Omega B_p}{2c} \sin^2 \theta \tag{22}\]のようになります。 途中、\(r=R\)として、中性子星表面での静電ポテンシャルの値を求めました。 すると、角度\(\theta_A, \theta_B\)間の電位差は
\[\Delta \Phi = \Phi_B - \Phi_A = \frac{R^2 \Omega B_p}{2c} (\sin^2 \theta_B - \sin^2 \theta_A) \tag{23}\]のようになります。
磁力線と中性子星中心との距離は
のように書けます。 ここで\(K\)は、各電気力線に依存する距離の次元を持つ変数です。
光円柱を超えた領域では、共回転速度\(v_\varphi = r\Omega\)が光速を超えるため、共回転は不可能となります。 このとき、粒子は助力線に沿った方向にも運動し、光円柱を超えて流出することになります。 同時に、磁力線は\(\phi\)方向成分(トロイダル成分)ももち、\(r, \theta\)方向(ポロイダル)電流が流れることになります。 磁力線は無限遠に向かって開いた構造となり、これをパルサー風と呼びます。 これに対して、共回転する閉じた磁力線は、共回転半径より小さい半径で赤道面を通過し、再び中性子星表面に戻ります。 このとき、閉じた共回転磁気圏と開いた助力線領域の境界を表す角度\(\theta_\mathrm{max}\)を求めてみましょう。 これは(24)式において、\(K = R_l = c/\Omega, r=R\)とすることで計算できます。
開いた磁力線を持つ\(\theta \leq \theta_\mathrm{max}\)を polar cap region と呼びます。 \(\theta =0\)と\(\theta=\theta_\mathrm{max}\)での電位差は、(23)式より
\[\Delta \Phi = \frac{R^2 \Omega B_p}{2c} \sin^2 \theta_\mathrm{max} = \frac{R^2 \Omega B_p}{2c} \frac{R}{R_l} = \frac{B_p R}{2} \left( \frac{\Omega R}{c}\right)^2 \tag{26}\]となります。 この電位差により電荷\(Ze\)を持つ荷電粒子が加速される場合に得られるエネルギーは、大雑把に
\[E_\mathrm{max} \approx 2\pi^2 B_p R \left(\frac{\Omega}{2\pi}\right)^2 \frac{R^2}{c^2} Ze \approx 6 \times 10^{12} \frac{Z B_{12} R_6^3}{P^2} \ [\mathrm{eV}] \tag{27}\]のように計算できます。 ここで\(R_6 = \frac{R}{10^6\mathrm{cm}}\)です。
パルサー磁気圏と単極誘導
ここまでの議論から、パルサー磁気圏中の電場は、次の式から求められたのでした。
\[\mathbf{E}^\mathrm{(out)} = - (\boldsymbol{\Omega} \times \mathbf{r}) \times \frac{\mathbf{B}^\mathrm{(out)}}{c} \tag{28}\]この式をよく眺めてみると、これは単極誘導により発生する電位差の式と同じであることがわかります。
\[V = \int_O^P (\boldsymbol{\omega} \times \mathbf{r}) \times \mathbf{B} \cdot d \mathbf{r} \tag{29}\]ここで注意したいのは、単極誘導のときは回路による閉曲路を考えていましたが、中性子星磁気圏のような場合にはそのような回路を考えていない点です。 回転する磁気力線で単極誘導を説明しようとすると、導線・電圧計・円盤で電気回路が閉じていることが本質となります。 しかし場と近接相互作用的な考え方では、空間の属性としての磁場が、座標変換により
\[\mathbf{E}' = \mathbf{E} + (\boldsymbol{\Omega} \times \mathbf{r}) \times \frac{\mathbf{B}}{c} \tag{30}\]に従う電場として観測されているに過ぎません。 したがって回路を閉じる必要はなく、単極誘導で使用されている導体円盤は本質ではなくなります。 導体は起電力を定義するための積分経路、もしくは電子の移動経路を決定しているに過ぎず、そこにたまたま自由電子を供給できる導体があることで、電流が流れることになります。 以上から、単極誘導がパルサー磁気圏のような自由空間にも適用可能であり、これがパルサー磁気圏・星雲を明るく輝かせるエネルギー源になっていると考えることができます。
参考文献
[1] Goldreich & Julian, 1969, “Pulsar electrodynamics”
[2] Shapiro & Teukolsky, ”Black holes white dwarfs and neutron stars”
[3] 高原文郎, “宇宙物理学”
[4] 高原文郎, “特殊相対論”
[5] 柴田晋平, “宇宙の灯台 パルサー”
[6] 中村哲, 須藤彰三, “電磁気学”
[7] 高橋秀俊, “電磁気学”