Table of contents
エピサイクリック運動
運動方程式
銀河中を運動する天体について考えましょう。 簡単のため銀河は軸対称であるとし、銀河の重力ポテンシャルは\(\Phi (R, z)\)のように書けるとします。 すると、この天体の運動方程式は
\[\frac{d^2 \mathbf{r}}{dt^2} = - \nabla \Phi (R, z) \tag{1}\]のように書けます。 これを\((R, \varphi, z)\)の円筒座標系で考えると
\[R方向: \ \ddot{R} - r\dot{\varphi}^2 = - \frac{\partial \Phi}{\partial R} \tag{2}\] \[\varphi 方向: \ \frac{d}{dt} (R^2 \dot{\varphi}) = 0 \tag{3}\] \[z 方向: \ \ddot{z} = - \frac{\partial \Phi}{\partial z} \tag{4}\]のようになります。 (3)式より
\[R^2 \dot{\varphi} = L_z \qquad (L_z: 定数) \tag{5}\]のように、角運動量保存が導かれます。 (5)式を用いて、\(\dot{\varphi}\)を消去しましょう。 すると(2)式は
\[\ddot{R} - \frac{L_z^2}{R^3} = - \frac{\partial \Phi}{\partial R} \ \Longrightarrow \ \ddot{R} = -\frac{\partial \Phi_\mathrm{eff}}{\partial R} \qquad \left( \Phi_\mathrm{eff} \equiv \Phi (R, z) + \frac{L_z^2}{2R^2}\right) \tag{6}\]のように整理されます。 \(\Phi_\mathrm{eff}\)を有効ポテンシャルと呼びます。
天体が円運動をしている場合
ここでは天体は、銀河中心から一定の半径\(R_g\)を円運動しているとしましょう。 すると(6)式において、動径方向の加速度がゼロであることより
\[\ddot{R} = -\frac{\partial \Phi_\mathrm{eff}}{\partial R} = 0 \ \Longrightarrow \ \left. \frac{\partial \Phi}{\partial R} \right|_{R=R_g} = \frac{L_z^2}{R_g^3} \tag{7}\]を得ます。 ここまで\(z\)成分についてはあまり議論してきませんでしたが、円盤銀河のような上下の対称性も持つようなでは\(z=0\)平面において\(\ddot{z}=0\)と考えることができます。 もし\(\ddot{z}\neq 0\)でない値を持つなら、天体は直ちに\(z\)方向に加速され、上下の対称性が保たれないためです。 数学的に言うならば、関数\(\Phi(R, z)\)は、\(z=0\)で極値を持つと言えます。
天体が円運動から少しずれている場合
次に、円運動している天体に摂動を加え、円運動から少しずれているような場合を考えましょう。 円運動からの摂動を以下のように表現します。
\[\left\{ \begin{array}{ll} R = R_g + x & (\vert x\vert \ll R_g) \\ \vert z \vert \ll 1 \end{array} \right. \tag{8}\]すると、この位置での有効ポテンシャルは
\[\begin{align} \Phi_\mathrm{eff} (R, z) &= \Phi_\mathrm{eff} (R_g, 0) + \underbrace{\left. \frac{\partial \Phi_\mathrm{eff}}{\partial R} \right|_{(R_g, 0)}}_{=0} x + \frac{1}{2} \left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial R^2} \right|_{(R_g, 0)} x^2 + \cdots \notag \\ & \quad + \underbrace{\left. \frac{\partial \Phi_\mathrm{eff}}{\partial z} \right|_{(R_g, 0)}}_{=0} z + \frac{1}{2} + \left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial z^2} \right|_{(R_g, 0)} z^2 + \cdots \notag \\ & \quad + \underbrace{\left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial R \partial z} \right|_{(R_g, 0)}}_{=0} xz + \cdots \tag{9} \end{align}\]のようになります。 途中、\(z=0\)平面内での円運動時の値から、いくつかの項の係数をゼロとしました。 以上より、摂動\(x\)についての運動方程式が
\[\ddot{r} = \ddot{x} = - \frac{\partial \Phi_\mathrm{eff}}{\partial R} = - \frac{\partial \Phi_\mathrm{eff}}{\partial x} = - \left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial R^2 } \right|_{(R_g, 0)} x \ \Longrightarrow \ \ddot{x} = -\kappa^2 x \qquad \left( \kappa^2 \equiv \left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial R^2 } \right|_{(R_g, 0)} \right) \tag{10}\]と求まります。 同様に\(z\)についても
\[\ddot{z} = -\nu^2 z \qquad \left( \nu^2 \equiv \left. \frac{\partial^2 \Phi_\mathrm{eff}}{\partial z^2 } \right|_{(R_g, 0)} \right) \tag{11}\]となります。 このことから、\(x, z\)は単振動する解とわかります。 (6), (10)式から\(\kappa^2\)を計算しましょう。
\[\frac{\partial \Phi_\mathrm{eff}}{\partial R} = \frac{\partial \Phi}{\partial R} - \frac{L_z^2}{R^3} \ \Longrightarrow \ \frac{\partial^2 \Phi_\mathrm{eff}}{\partial R^2} = \frac{\partial^2 \Phi}{\partial R^2} + \frac{3 L_z^2}{R^4} \tag{12}\]ここで(5)式より、円運動における角速度を\(\Omega\)とすると
\[\Omega (R) = \frac{L_z}{R^2} \tag{13}\]から
\[\frac{\partial^2 \Phi_\mathrm{eff}}{\partial R^2} = \frac{\partial^2 \Phi}{\partial R^2} + 3 \Omega^2 \tag{13}\]のように変形されます。 さらに円運動において、遠心力と重力は等しくなければならないため
\[R \Omega^2 = \frac{\partial \Phi}{\partial R} \ \Longrightarrow \ \frac{\partial^2 \Phi}{\partial R^2} = \Omega^2 + R \frac{d\Omega^2}{dR} \tag{14}\]を得ます。 以上より
\[\kappa^2 = R \frac{d \Omega^2}{dR} + 4 \Omega^2 \tag{15}\]と整理されます。 例えば、剛体回転する系では\(\Omega (R) = (一定)\)より\(\kappa=2\Omega\)、ケプラー回転では\(\Omega (R) \propto R^{-3/2}\)より\(\kappa = \Omega\)などとなります。 (15)式からもわかるように、重力により差動回転しているような系では\(\Omega \leq \kappa \leq 2\Omega\)程度になります。
(10)式の解を計算しましょう。 単振動の式に一致していることから、動径方向に関しては
です。 そして方位角方向に関しては
\[\dot{\varphi} = \frac{L_z}{(R_g + x)^2} = \frac{L_z}{R_g^2 (1+x/R_g)^2} \approx \frac{L_z}{R_g^2} \left( 1-\frac{2x}{L_g}\right) = \Omega \left( 1-\frac{2x}{L_g}\right) \tag{17}\]を積分することで
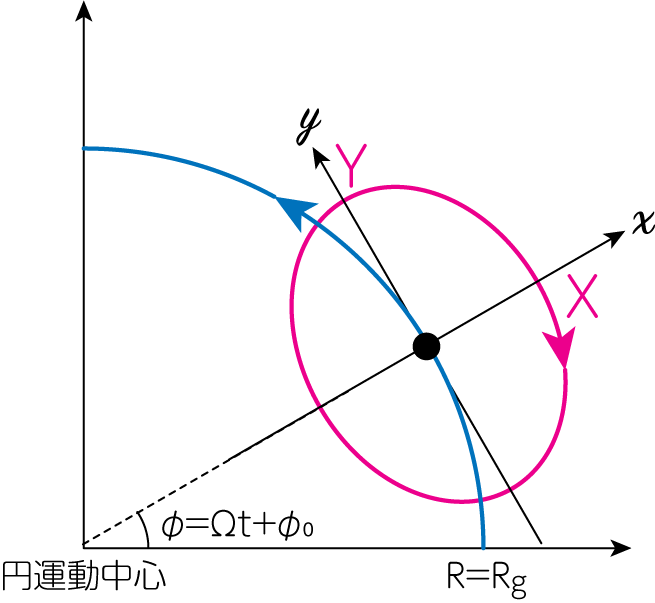
\[\varphi (t) = \Omega t - \frac{2 \Omega X}{R_g \kappa} \sin(\kappa t + \psi) + \varphi_0 \qquad (\varphi_0 は定数) \tag{18}\]のようになります。 (18)式の第二項は、(16)式と位相が\(\pi/2\)ズレている表式をしているとわかります。 このことから、この部分は\(x\)に直交する\(y/R_g\)と考えることができます。 すると
\[y = - \frac{2\Omega X}{\kappa} \sin (\kappa t + \psi) = - Y \sin (\kappa t + \psi) \qquad \left(Y \equiv \frac{2\Omega X}{\kappa} \right) \tag{19}\](16), (19)式より
\[\left( \frac{x}{X} \right) + \left( \frac{y}{Y}\right)^2 = 1 \tag{20}\]のように、楕円の方程式を得ることができます。 また\(\Omega \leq \kappa \leq 2\Omega\)より
\[\frac{X}{Y} = \frac{\kappa}{2\Omega} \leq 1 \tag{21}\]のように、\(y\)方向に伸びた楕円軌道となることがわかります。
\(z\)方向の運動
同様に\(z\)方向についても調べてみましょう。 (11)式より
\[z = Z \cos (\nu t + \zeta) \tag{22}\]とわかります。 ここで、ポアソン方程式を見てみましょう。
\[\frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Phi}{\partial R}\right) + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho \tag{23}\]そして遠心力と重力の釣り合いより
\[\frac{v_c^2}{R} = \frac{\partial \Phi}{\partial R} \tag{24}\]を代入しましょう。 すると
\[\frac{1}{R} \frac{dv_c^2}{dR} + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho \tag{25}\]となります。 円盤銀河の場合、flat rotationから\(\frac{dv_c^2}{dR} \sim 0\)と考えることができます。 よって、\(z\)方向の振動数は
\[\nu^2 \approx 4\pi G \rho \tag{26}\]のようになります。 円盤銀河では、\(z=0\)に質量が集まっていることが知られています。 \(z=0\)から少し外れると\(\rho\)が急激に減少するため、現実的には\(\nu\)は一定ではありません。 よって\(z\)方向に対するこのような近似は、\(Z \leq 100 \mathrm{pc}\)にいるような若い恒星や散開星団にしか適用できないことに注意しましょう。
参考文献
[1] Binney & Tremaine, “Galactic Dynamics: Second Edition”
[2] Bovy, “Dyanmics and Astrophysics of Galxies”
[3] 福江純, 和田桂一, 梅村雅之, “宇宙流体力学の基礎”