Table of contents
恒星内部でのエネルギー保存
恒星内部でのエネルギーの交換は、準静的に起こるとします。 するとある単位体積に対するエネルギー保存は、熱力学の法則
\[d'Q = \rho T dS \tag{6.1.1}\]の関係から導くことができます。 ここで\(d'Q\)は単位体積あたりにガスが吸収する熱エネルギー、\(S\)は単位質量あたりのエントロピーを表します。 恒星内部のガスに上の関係を適用すると
\[- \nabla \cdot \mathbf{F} + \rho (\epsilon_n - \epsilon_\nu) = \rho T \frac{dS}{dt} \tag{6.1.2}\]のようになります。 ここで\(\nabla \cdot \mathbf{F}\)はエネルギー流束\(\mathbf{F}\)による単位体積あたりのエネルギーの損失率、\(\epsilon_\mathrm{n}\)は核反応による単位質量あたりのエネルギー発生率、\(\epsilon_\nu\)はニュートリノの発生による単位質量あたりのエネルギー損失率です。 ニュートリノは超新星爆発などを除き、通常は恒星内のガスと相互作用せず、発生すると光速度に近い速度で恒星外に出てしまうのでエネルギーの損失となります。 球対称の場合
\[\nabla \cdot \mathbf{F} = \frac{1}{r^2} \frac{d}{dr} (r^2 F_r) = \frac{1}{4\pi r^2} \frac{d}{dr} (4\pi r^2 F_r) = \frac{1}{4\pi r^2} \frac{dL_r}{dr}\]のように書けるため、(6.1.2)式は
\[- \frac{1}{4\pi r^2} \frac{dL_r}{dr} + \rho (\epsilon_\mathrm{n} - \epsilon_\nu) = \rho T \frac{dS}{dt}\]となります。 ここで\(L_r\)は中心から\(r\)の距離にある球面を、単位時間あたりに通過するエネルギーを表します。 上式に\(dM_r = 4\pi r^2 \rho dr\)の関係を用いると、\((M_r, t)\)を独立変数としたときの\(L_r\)に対する微分方程式
\[\frac{dL_r}{dM_r} = \epsilon_\mathrm{n} - \epsilon_\nu - T \frac{dS}{dt} \tag{6.1.3}\](6.1.3)式の図を用いた導出
この式は以下のように導出することもできます。
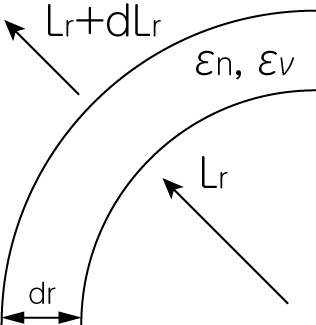
恒星中心からの距離\(r\)と\(r + dr\)の球に挟まれた球殻部分を考えます。 殻の内側の面からのエネルギー流入率を\(L_r\)、外側の面か単位時間あたり出ていくエネルギーを\(L_r + dL_r\)とします。 また単位質量あたりのエントロピーを\(S\)とし、球殻中での単位質量あたりの核融合による熱の発生率を\(\epsilon_\mathrm{n}\)、そして単位質量あたりのニュートリノ発生率を\(\epsilon_\nu\)としましょう。 すると球殻に対するエネルギー保存の式は
\[\rho T \frac{dS}{dt} 4\pi r^2 dr = 4\pi r^2 dr \rho (\epsilon_\mathrm{n} - \epsilon_\nu) + L_r - (L_r + dL_r)\]のようになります。 この両辺を\(dM_r = 4\pi r^2 \rho dr\)で割れば、(6.1.3)式を得ます。
参考文献
[1] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[2] 高原文郎, “宇宙物理学”
[3] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”