測地線方程式

重力のみが働く粒子は測地線を通ることを用いて、より一般的な、重力場中での粒子の運動方程式を導出します。

導出

質量\(m\neq 0\)の粒子が軌跡\({\bf x}(\tau)\)を描いて運動しているとします。

\[ds^2 = g_{\mu \nu} dx^\mu dx^\nu = -c^2 d\tau^2 = -c^2 dt^2 + d{\bf x}^2\]

ここで

\[d\tau = dt\sqrt{1-\frac{1}{c^2} \frac{d {\bf x}^2}{dt^2}} = dt \sqrt{1-\frac{v^2}{c^2}} \underbrace{=}_{\beta \equiv v/c} dt \sqrt{1-\beta^2} = \frac{dt}{\gamma}\]

そして4元速度を

\[{\bf u} \equiv \frac{d{\bf x}(\tau)}{d\tau}, \ u^\mu \equiv \frac{dx^\mu}{d\tau}\]

のように、軌跡の接ベクトルとして定義します。

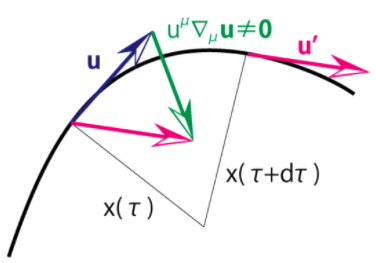
軌跡に沿った方向の微分のイメージ

今、粒子には重力しか働いていないと考えましょう。慣性系では必ず重力を打ち消すことができるので、粒子は慣性系で等速直線運動になるはずです。よって速度\({\bf u}\)に沿った方向への微分\(u^\mu \nabla_\mu\)を考えると

\[u^\mu \nabla_\mu {\bf u} = {\bf 0}\]

となるはずです。これを測地線方程式と呼びます。重力のみが働く粒子は測地線(慣性系での等速直線運動の軌跡)を通ります。
共変微分より

\[\begin{aligned} &u^\mu \partial_\mu u^\nu + u^\mu \Gamma^\nu_{\alpha \mu} u^\alpha = 0 \ \Longrightarrow \ \frac{dx^\mu}{d\tau} \frac{\partial u^\nu}{\partial x^\mu} + \Gamma^\nu_{\alpha \mu} u^\mu u^\alpha = \frac{dx^\nu}{d \tau} + \Gamma^\nu_{\alpha \mu} u^\mu u^\alpha = 0 \\ &\Longrightarrow \ \frac{du^\nu}{d\tau} = -\Gamma^\nu_{\alpha \mu} u^\mu u^\alpha \end{aligned}\]

最後の式の左辺が加速度、右辺が重力を表しています。