HLLD法
ここでは(磁気)流体力学の計算手法であるHLLD法についての勉強メモを記述しています。
磁気流体方程式群
用いる方程式はHLL法, HLLC法で考えたものと同じです。
\[\frac{\partial}{\partial t} \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \\ B_x \\ B_y \\ B_z \end{array} \right) + \frac{\partial}{\partial x} \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot} - B_x^2 \\ \rho v_y v_x - B_y B_x\\ \rho v_z v_x - B_z B_x\\ (E + P_\mathrm{tot}) v_x - (\mathbf{B} \cdot \mathbf{v}) B_x \\ 0 \\ B_y v_x - v_y B_x \\ B_z v_x - v_z B_x \end{array}\right) = \frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} = \mathbf{0} \tag{1}\]流束計算
HLL法では中間状態を1つ、HLLC法では中間状態を2つ用意しました。 今回考えるHLLD法では、磁場により発生するアルヴェーン波の伝播も考えます。よって下図のように4つの中間状態を考えます。
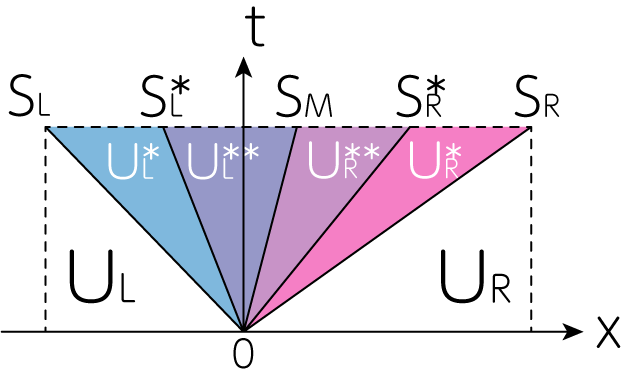
このとき、\(v_x\)の中間状態である\(v_{x, L}^\ast, v_{x, L}^{\ast \ast}, v_{x, R}^{\ast \ast}, v_{x, R}^\ast\)は全て等しい(上図でリーマンファンと呼ばれる色のついた4つの部分で値が一定である)と仮定します。
\[v_{x, L}^\ast = v_{x, L}^{\ast \ast} = v_{x, R}^{\ast \ast} = v_{x, R}^\ast = S_M \tag{2}\]ここで\(S_M\)はHLLC法と同様に、HLL中間状態から求めます。すなわち
\[\mathbf{U}_\mathrm{HLL}^\ast = \frac{S_R \mathbf{U}_R - S_L \mathbf{U}_L - \mathbf{F}_R + \mathbf{F}_L}{S_R - S_L} \tag{3}\]から
\[\rho_\mathrm{HLL}^\ast = \frac{S_R \rho_R - S_L \rho_L - \rho_R v_{x, R} + \rho_L v_{x, L}}{S_R - S_L} \tag{4}\] \[\begin{align} (\rho v_x)_\mathrm{HLL}^\ast &= \frac{S_R \rho_R v_{x, R} - S_L \rho_L v_{x, L} - (\rho_R v_{x, R} v_{x, R} + P_{\mathrm{tot}, R} - B_x^2) + (\rho_L v_{x, L} v_{x, L} + P_{\mathrm{tot}, L} - B_x^2)}{S_R - S_L} \notag \\ &= \frac{S_R \rho_R v_{x, R} - S_L \rho_L v_{x, L} - (\rho_R v_{x, R} v_{x, R} + P_{\mathrm{tot}, R}) + (\rho_L v_{x, L} v_{x, L} + P_{\mathrm{tot}, L})}{S_R - S_L} \tag{5} \end{align}\]を求めておいて
\[S_M = \frac{(\rho v_x)_\mathrm{HLL}^\ast}{\rho_\mathrm{HLL}^\ast} = \frac{(S_R - v_{x, R}) \rho_R v_{x, R} - (S_L - v_{x, L}) \rho_L v_{x, L} - P_{\mathrm{tot}, R} + P_{\mathrm{tot}, L}}{(S_R - v_{x, R})\rho_R -(S_L-v_{x, L}) \rho_L} \tag{6}\]のように計算します。さらに全圧力も一定であるとします。
\[P_{\mathrm{tot}, L}^\ast = P_{\mathrm{tot}, L}^{\ast \ast} = P_{\mathrm{tot}, R}^{\ast \ast} = P_{\mathrm{tot}, R}^\ast = P_\mathrm{tot}^\ast \tag{7}\] \[P_\mathrm{tot}^\ast = P_{\mathrm{tot}, R} + \rho_R (S_R - v_{x, R}) (S_M - v_{x, R}) \tag{8}\]と計算されますが、これをさらに式変形しましょう。(6)式より
\[\begin{align} S_M - v_{x, R} &= \frac{(S_R - v_{x, R}) \rho_R v_{x, R} - (S_L - v_{x, L}) \rho_L v_{x, L} - P_{\mathrm{tot}, R} + P_{\mathrm{tot}, L} - (S_R - v_{x, R}) \rho_R v_{x, R} + (S_L - v_{x, L}) \rho_L v_{x, R}}{(S_R - v_{x, R})\rho_R -(S_L-v_{x, L}) \rho_L} \notag \\ &= \frac{(S_L - v_{x, L}) \rho_L (v_{x, R} - v_{x, L}) - P_{\mathrm{tot}, R} + P_{\mathrm{tot}, L}}{(S_R - v_{x, R})\rho_R -(S_L-v_{x, L}) \rho_L} \tag{9} \end{align}\]のように計算できるので
\[\begin{align} P_\mathrm{tot}^\ast &= P_{\mathrm{tot}, R} + \frac{\rho_R (S_R - v_{x, R}) (S_L - v_{x, L}) \rho_L (v_{x, R} - v_{x, L}) - \rho_R (S_R - v_{x, R}) P_{\mathrm{tot}, R} + \rho_R (S_R - v_{x, R}) P_{\mathrm{tot}, L}}{(S_R - v_{x, R}) \rho_R - (S_L - v_{x, L}) \rho_L} \notag \\ &= \frac{\rho_R (S_R - v_{x, R}) (S_L - v_{x, L}) \rho_L (v_{x, R} - v_{x, L}) + \rho_R (S_R - v_{x, R}) P_{\mathrm{tot}, L} - (S_L - v_{x, L}) \rho_L P_{\mathrm{tot}, R}}{(S_R - v_{x, R}) \rho_R - (S_L - v_{x, L}) \rho_L} \tag{10} \end{align}\]先程(7)式で仮定した\(P_{\mathrm{tot}, L}^{\ast \ast} = P_{\mathrm{tot}, R}^{\ast \ast} = P_{\mathrm{tot}}^{\ast}\)は自動で満たされます(これについては後述)。またこの仮定をおいても、接触不連続面・接戦不連続面・回転不連続面は正しく計算されます。
\(S_M, P_\mathrm{tot}^\ast\)が計算できたので、これらを用いて\(S_\alpha\)でのジャンプ条件から様々な値を求めましょう。
(11)式の第一式より
\[(S_\alpha - S_M) \rho_\alpha^\ast = (S_\alpha - v_{x, \alpha}) \rho_\alpha \ \Longrightarrow \ \rho_\alpha^\ast = \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} \rho_\alpha \tag{12}\]これはHLLC法のときと同じです。第六式より
\[S_\alpha B_{y, \alpha}^\ast - B_{y, \alpha}^\ast S_M + v_{y, \alpha}^\ast B_x = S_\alpha B_{y, \alpha} - B_{y, \alpha} v_{x, \alpha} + v_{y, \alpha} B_x \ \Longrightarrow \ B_{y, \alpha}^\ast = \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} B_{y, \alpha} + \frac{v_{y, \alpha} - v_{y, \alpha}^\ast}{S_\alpha - S_M} B_x \tag{13}\]これと第三式より
\[\begin{aligned} &S_\alpha \rho_\alpha^\ast v_{y, \alpha}^\ast - \rho_\alpha^\ast v_{y, \alpha}^\ast S_M + B_{y, \alpha}^\ast B_x = S_\alpha \rho_\alpha v_{y, \alpha} - \rho_\alpha v_{y, \alpha} v_{x, \alpha} + B_{y, \alpha} B_x \\ &\Longrightarrow \ (S_\alpha - S_M) \underbrace{\rho_\alpha^\ast}_{(12)} v_{y, \alpha}^\ast + \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - S_M} B_{y, \alpha} B_x + \frac{v_{y, \alpha} - v_{y, \alpha}^\ast}{S_\alpha - S_M} B_x^2 = (S_\alpha - v_{x, \alpha}) \rho_\alpha v_{y, \alpha} + B_{y, \alpha} B_x \\ &\Longrightarrow \ (S_\alpha - v_{x, \alpha}) \rho_\alpha v_{x, \alpha}^\ast = (S_\alpha - v_{x, \alpha}) \rho_\alpha v_{y, \alpha} + \frac{v_{x, \alpha} - S_M}{S_\alpha - S_M} B_{y, \alpha} B_x - \frac{B_x^2}{S_\alpha - S_M} v_{y, \alpha} + \frac{B_x^2}{S_\alpha - S_M} v_{y, \alpha}^\ast \\ &\Longrightarrow \ \frac{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2}{S_\alpha - S_M} v_{y, \alpha}^\ast = \frac{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2}{S_\alpha - S_M} v_{y, \alpha} + \frac{v_{x, \alpha} - S_M}{S_\alpha - S_M} B_{y, \alpha} B_x \end{aligned}\]以上より
\[v_{y, \alpha}^\ast = v_{y, \alpha} - \frac{S_M - v_{x, \alpha}}{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2} B_{y, \alpha} B_x \tag{14}\]を得ます。(14)式を先程の第六式の関係に用いると
\[\begin{align} &(S_\alpha - S_M) B_{y, \alpha}^\ast + B_x v_{y, \alpha} - \frac{S_M - v_{x, \alpha}}{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2} B_{y, \alpha} B_x^2 = (S_\alpha - v_{x, \alpha}) B_{y, \alpha} + v_{y, \alpha} B_x \notag \\ &\Longrightarrow \ (S_\alpha - S_M) B_{y, \alpha}^\ast = \frac{B_{y, \alpha} B_x^2 (S_M - v_{x, \alpha}) + (S_\alpha - v_{x, \alpha}) B_{y, \alpha} \{ (S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2\}}{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2} \notag \\ & \qquad \qquad \qquad = B_{y, \alpha} \frac{(S_\alpha - v_{x, \alpha})^2 (S_\alpha - S_M) \rho_\alpha - B_x^2 (S_\alpha- S_M)}{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) - B_x^2} \notag \\ &\Longrightarrow \ B_{y, \alpha}^\ast = B_{y, \alpha} \frac{\rho_\alpha (S_\alpha - v_{x, \alpha})^2 - B_x^2}{\rho_\alpha (S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) - B_x^2} \tag{15} \end{align}\]同様に第四式と第七式から\(v_{z, \alpha}^\ast, B_{z, \alpha}^\ast\)を求めましょう。同じように式変形すれば、(14), (15)式において\(v_{y, \alpha} \rightarrow v_{z, \alpha}, B_{y, \alpha} \rightarrow B_{z, \alpha}\)とした結果を得ることができます。
\[v_{z, \alpha}^\ast = v_{z, \alpha} - \frac{S_M - v_{x, \alpha}}{(S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) \rho_\alpha - B_x^2} B_{y, \alpha} B_x \tag{16}\] \[B_{z, \alpha}^\ast = B_{z, \alpha} \frac{\rho_\alpha (S_\alpha - v_{x, \alpha})^2 - B_x^2}{\rho_\alpha (S_\alpha - v_{x, \alpha}) (S_\alpha - S_M) - B_x^2} \tag{17}\](14)-(17)式は、\(S_M = v_{x, \alpha}, S_\alpha = v_{x, \alpha} \pm c_{f, \alpha}, B_{y, \alpha} = B_{z, \alpha} = 0, B_x^2 \geq \gamma P_\alpha\)などを満たす場合に、\(0/0\)の不定形になる場合があります。 このときはシンプルに(12)式などから\(\rho_\alpha^\ast = \rho_\alpha, v_{x, \alpha}^\ast = v_{x, \alpha}, P_{\mathrm{tot}, \alpha}^\ast = P_{\mathrm{tot}, \alpha}\)です。 よって\(v_{y, \alpha}^\ast = v_{y, \alpha}, v_{z, \alpha}^\ast = v_{z, \alpha}, B_{y, \alpha}^\ast = B_{z, \alpha}^\ast = 0\)となります。 このときは\(\rho_\alpha^\ast = \rho_\alpha\)などからわかるように、衝撃波ではありません。
続けてエネルギーを求めてみましょう。(11)式の第五式より
と求まります。これでアスタリスクが一つ付いた物理量が全て求まりました。続いてアスタリスクが2つの物理量を求めていきましょう。\(v_{x, L}^{\ast} = v_{x, L}^{\ast \ast} = v_{x, R}^{\ast \ast} = v_{x, R}^\ast = S_M\)の仮定から、\(S_L < S< S_M\)または\(S_M <S< S_R\)を満たす\(S\)に対する質量保存則からジャンプ条件を式変形し
\[S \rho_\alpha^{\ast \ast} - \rho_\alpha^{\ast \ast} S_M = S \rho_\alpha^\ast - \rho_\alpha^\ast S_M \ \Longrightarrow \ \rho_\alpha^{\ast \ast} = \rho_\alpha^\ast \tag{19}\]を得ます。続いて\(x\)方向の運動量保存則より
\[S \rho_\alpha^{\ast \ast} S_M - \rho_\alpha^{\ast \ast} S_M S_M - P_{\mathrm{tot}, \alpha}^{\ast \ast} + B_x^2 = S \rho_\alpha^\ast S_M - \rho_\alpha^\ast S_M S_M - P_{\mathrm{tot}, \alpha}^\ast + B_x^2 \ \Longrightarrow \ P_{\mathrm{tot}, \alpha}^{\ast \ast} = P_{\mathrm{tot}, \alpha}^\ast \tag{20}\]ここではあえて\(P_\mathrm{tot}^\ast\)を\(P_{\mathrm{tot}, \alpha}^\ast \ (\alpha = R, L)\)のように書き分けています。しかし\(S_M\)は接触不連続面であるため、\(P_{\mathrm{tot}, L}^{\ast \ast} = P_{\mathrm{tot}, R}^{\ast \ast}\)が成り立ちます。このことと(20)式から、(7)式の仮定が正しいことがわかります。
(19)式から、左方向・右方向に進むアルヴェーン波の速度として
が適切であることがわかります。それでは、この\(S_\alpha^\ast \ (\alpha = L, R)\)の波面でのジャンプ条件を考えましょう。
\[S_\alpha^\ast \left( \begin{array}{c} \rho_\alpha^{\ast \ast} v_{y, \alpha}^{\ast \ast} \\ \rho_\alpha^{\ast \ast} v_{z, \alpha}^{\ast \ast} \\ B_{y, \alpha}^{\ast \ast} \\ B_{z, \alpha}^{\ast \ast} \end{array}\right) - \left( \begin{array}{c} \rho_\alpha^{\ast \ast} v_{y, \alpha}^{\ast \ast} S_M - B_{y, \alpha}^{\ast \ast} B_x \\ \rho_\alpha^{\ast \ast} v_{z, \alpha}^{\ast \ast} S_M - B_{z, \alpha}^{\ast \ast} B_x \\ B_{y, \alpha}^{\ast \ast} S_M - v_{y, \alpha}^{\ast \ast} B_x \\ B_{z, \alpha}^{\ast \ast} S_M - v_{z, \alpha}^{\ast \ast} B_x \end{array}\right) = S_\alpha^\ast \left( \begin{array}{c} \rho_\alpha^{\ast} v_{y, \alpha}^{\ast} \\ \rho_\alpha^{\ast} v_{z, \alpha}^{\ast} \\ B_{y, \alpha}^{\ast} \\ B_{z, \alpha}^{\ast} \end{array}\right) - \left( \begin{array}{c} \rho_\alpha^{\ast} v_{y, \alpha}^{\ast} S_M - B_{y, \alpha}^{\ast} B_x \\ \rho_\alpha^{\ast} v_{z, \alpha}^{\ast} S_M - B_{z, \alpha}^{\ast} B_x \\ B_{y, \alpha}^{\ast} S_M - v_{y, \alpha}^{\ast} B_x \\ B_{z, \alpha}^{\ast} S_M - v_{z, \alpha}^{\ast} B_x \end{array}\right) \tag{22}\]同様に\(S_M\)でのジャンプ条件を考えます。
\[S_M \left( \begin{array}{c} \rho_L^{\ast \ast} v_{y, L}^{\ast \ast} \\ \rho_L^{\ast \ast} v_{z, L}^{\ast \ast} \\ B_{y, L}^{\ast \ast} \\ B_{z, L}^{\ast \ast} \end{array}\right) - \left( \begin{array}{c} \rho_L^{\ast \ast} v_{y, L}^{\ast \ast} S_M - B_{y, L}^{\ast \ast} B_x \\ \rho_L^{\ast \ast} v_{z, L}^{\ast \ast} S_M - B_{z, L}^{\ast \ast} B_x \\ B_{y, L}^{\ast \ast} S_M - v_{y, L}^{\ast \ast} B_x \\ B_{z, L}^{\ast \ast} S_M - v_{z, L}^{\ast \ast} B_x \end{array}\right) = S_M \left( \begin{array}{c} \rho_R^{\ast \ast} v_{y, R}^{\ast \ast} \\ \rho_R^{\ast \ast} v_{z, R}^{\ast \ast} \\ B_{y, R}^{\ast \ast} \\ B_{z, R}^{\ast \ast} \end{array}\right) - \left( \begin{array}{c} \rho_R^{\ast \ast} v_{y, R}^{\ast \ast} S_M - B_{y, R}^{\ast \ast} B_x \\ \rho_R^{\ast \ast} v_{z, R}^{\ast \ast} S_M - B_{z, R}^{\ast \ast} B_x \\ B_{y, R}^{\ast \ast} S_M - v_{y, R}^{\ast \ast} B_x \\ B_{z, R}^{\ast \ast} S_M - v_{z, R}^{\ast \ast} B_x \end{array}\right) \tag{23}\](23)式より
\[v_{y, L}^{\ast \ast} = v_{y, R}^{\ast \ast} = v_y^{\ast \ast}, \quad v_{z, L}^{\ast \ast} = v_{z, R}^{\ast \ast} = v_z^{\ast \ast} \tag{24}\] \[B_{y, L}^{\ast \ast} = B_{y, R}^{\ast \ast} = B_y^{\ast \ast}, \quad B_{z, L}^{\ast \ast} = B_{z, R}^{\ast \ast} = B_z^{\ast \ast} \tag{25}\]ただし、これは\(B_x \neq 0\)の場合です。もし\(B_x = 0\)の場合は、例えば(23)式の第一式より
\[S_M \rho_L^{\ast \ast} v_{y, L}^{\ast \ast} - \rho_L^{\ast \ast} v_{y, L}^{\ast \ast} S_M = S_M \rho_R^{\ast \ast} v_{y, R}^{\ast \ast} - \rho_R^{\ast \ast} v_{y, R}^{\ast \ast} S_M \ \Longrightarrow \ 0 = 0 \tag{*}\]のようになり、求めることができません(これに関しては後で詳細を述べます)。
次に、(24), (25)式で出てきた\(v_y^{\ast \ast}, v_z^{\ast \ast}, B_y^{\ast \ast}, B_z^{\ast \ast}\)を求めましょう。 そのために、以下のようにリーマンファンの周囲を周回積分を行います。
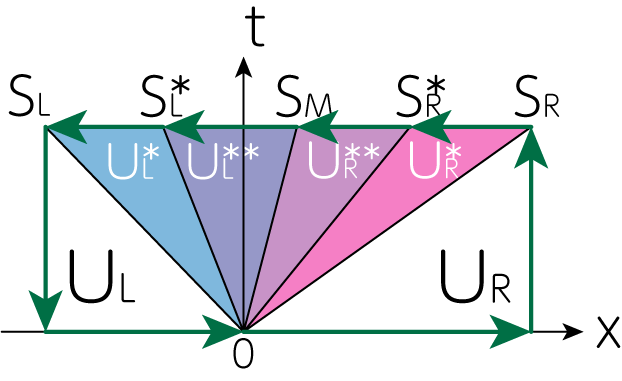
すると、以下の保存則を得ます。
\[S_R \Delta t \mathbf{U}_R - \mathbf{F}_R \Delta t - (S_R - S_R^\ast) \Delta t \mathbf{U}_R^\ast - (S_R^\ast - S_M) \Delta t \mathbf{U}_R^{\ast \ast} - (S_M - S_L^\ast) \Delta t \mathbf{U}_L^{\ast \ast} - (S_L^\ast - S_L) \Delta t \mathbf{U}_L^\ast + \mathbf{F}_L \Delta t - S_L \Delta t \mathbf{U}_L = \mathbf{0}\]この式と、\(S_R, S_L\)での保存則
\[S_R \mathbf{U}_R - \mathbf{F}_R = S_R \mathbf{U}_R^\ast - \mathbf{F}_R^\ast, \quad S_L \mathbf{U}_L - \mathbf{F}_L = S_L \mathbf{U}_L^\ast - \mathbf{F}_L^\ast\]より
\[\begin{align} &- \mathbf{F}_R^\ast + S_R^\ast \mathbf{U}_R^\ast - S_R^\ast \mathbf{U}_R^{\ast \ast} + S_M \mathbf{U}_R^{\ast \ast}- S_M \mathbf{U}_L^{\ast \ast} +S_L^\ast \mathbf{U}_L^{\ast \ast} - S_L^\ast \mathbf{U}_L^\ast + \mathbf{F}_L = \mathbf{0} \notag \\ &\Longrightarrow \ \underbrace{(S_M - S_R^\ast)}_{(21)} \mathbf{U}_R^{\ast \ast} + \underbrace{(S_L^\ast - S_M)}_{(21)} \mathbf{U}_L^{\ast \ast} - \mathbf{F}_R^{\ast} + \underbrace{S_R^\ast}_{(21)} \mathbf{U}_R^\ast - \underbrace{S_L^\ast}_{(21)} \mathbf{U}_L^\ast + \mathbf{F}_L^\ast = \mathbf{0} \notag \\ &\Longrightarrow \ - \frac{\vert B_x \vert}{\sqrt{\rho_R^\ast}} \mathbf{U}_R^{\ast \ast} - \frac{\vert B_x \vert}{\sqrt{\rho_L^\ast}} \mathbf{U}_L^{\ast \ast} - \mathbf{F}_R^\ast + \left( S_M + \frac{\vert B_x \vert}{\sqrt{\rho_R^\ast}}\right) \mathbf{U}_R^\ast - \left( S_M - \frac{\vert B_x \vert}{\sqrt{\rho_L^\ast}}\right) \mathbf{U}_L^\ast + \mathbf{F}_L^\ast = \mathbf{0} \tag{26} \end{align}\]ここに\(y\)方向の運動量保存則を適用します。\(U = \rho v_y, F = \rho v_y v_x - B_y B_x\)より
\[\begin{aligned} &- \frac{\vert B_x \vert}{\sqrt{\rho_R^\ast}} \rho_R^{\ast \ast} v_{y}^{\ast \ast} - \frac{\vert B_x \vert}{\sqrt{\rho_L^\ast}} \rho_L^{\ast \ast} v_y^{\ast \ast} - (\rho_R^\ast v_{y, R}^\ast S_M - B_{y, R}^\ast B_x) + \left( S_M + \frac{\vert B_x \vert}{\sqrt{\rho_R^\ast}}\right) \rho_R^\ast v_{y, R}^\ast - \left( S_M - \frac{\vert B_x \vert}{\sqrt{\rho_L^\ast}}\right) \rho_L^\ast v_{y, L}^\ast + (\rho_L^\ast v_{y, L}^\ast S_M - B_{y, L}^\ast B_x) = 0 \\ &\Longrightarrow \ - \vert B_x \vert (\sqrt{\rho_L^\ast} + \sqrt{\rho_R^\ast}) v_y^{\ast \ast} + B_{y, R}^\ast B_x + \vert B_x \vert \sqrt{\rho_L^\ast} v_{y, L}^\ast + \vert B_x \vert \sqrt{\rho_R^\ast} v_{y, R}^\ast - B_{y, L}^\ast B_x = 0 \end{aligned}\]ここで\(\mathrm{sign} (B_x) = B_x / \vert B_x \vert\)を用いると
\[v_y^{\ast \ast} = \frac{\sqrt{\rho_L^\ast} v_{y, L}^\ast + \sqrt{\rho_R^\ast} v_{y, R}^\ast + (B_{y, R}^\ast - B_{y, L}^\ast) \mathrm{sign} (B_x)}{\sqrt{\rho_L^\ast} + \sqrt{\rho_R^\ast}} \tag{27}\]を得ます。同様の式変形をしても良いですが、(27)式において\(v_y \rightarrow v_z, B_y \rightarrow B_z\)とすることで
\[v_z^{\ast \ast} = \frac{\sqrt{\rho_L^\ast} v_{z, L}^\ast + \sqrt{\rho_R^\ast} v_{z, R}^\ast + (B_{z, R}^\ast - B_{z, L}^\ast) \mathrm{sign} (B_x)}{\sqrt{\rho_L^\ast} + \sqrt{\rho_R^\ast}} \tag{28}\]を得ます。
今度は(26)式に誘導方程式の\(y\)成分を用います。すなわち\(U = B_y, F = B_y v_x - v_y B_x\)とすると
となります。同様の式変形をしても構いませんが、(29)式において\(v_y \rightarrow v_z, B_y \rightarrow B_z\)とすることで
\[B_z^{\ast \ast} = \frac{\sqrt{\rho_L^\ast} B_{z, R}^\ast + \sqrt{\rho_R^\ast} B_{z, L}^\ast + \sqrt{\rho_L^\ast \rho_R^\ast} (v_{z, R}^\ast - v_{z, L}^\ast) \mathrm{sign} (B_x) }{\sqrt{\rho_L^\ast} + \sqrt{\rho_R^\ast}} \tag{30}\]を得ます。
最後に\(E_\alpha^{\ast \ast}\)を求めましょう。\(S_\alpha^\ast\)に対するジャンプ条件より
となります。最後の複合は\(\alpha = L\)のときマイナス、\(\alpha = R\)のときプラスとなります。さらに\(\mathbf{v}_\alpha^{\ast \ast} = (S_M, v_y^{\ast \ast}, v_z^{\ast \ast}), \mathbf{B}_\alpha^{\ast \ast} = (B_x, B_y^{\ast \ast}, B_z^{\ast \ast})\)であることから、\(\mathbf{v}_L^{\ast \ast} = \mathbf{v}_R^{\ast \ast} = \mathbf{v}^{\ast \ast}, \mathbf{B}_L^{\ast \ast}= \mathbf{B}_R^{\ast \ast} = \mathbf{B}^{\ast \ast}\)であることを用いました。 これらを用いれば、求めたかった\(\mathbf{F}_L^{\ast \ast}, \mathbf{F}_R^{\ast \ast}\)が計算できたことになります。
最後に\(B_x \rightarrow 0\)の極限について触れておきましょう。このときは(21)式より\(S_L^\ast = S_R^\ast = S_M\)です。よってこれはHLLC法のように、中間状態を2つとしたときのソルバーに一致します。 このことから\(B_x =0\)では、そもそも\(\mathbf{U}_\alpha^{\ast \ast}, \mathbf{F}_\alpha^{\ast \ast}\)を考える必要がなく、(*)式の問題はそもそも出現しないことがわかります。
数値計算に用いる
HLL法, HLLC法と同様に、実際の数値計算では\(S_L, S_L^\ast, S_M, S_R^\ast, S_R\)の大きさに依存して、どの流束を用いるかを決定します。 下図は左上から\(S_L > 0, S_L \leq 0 < S_L^\ast, S_L^\ast \leq 0 < S_M, S_M \leq 0 < S_R^\ast, S_R^\ast \leq 0 < S_R, S_R \leq 0\)の場合を図示したものです。
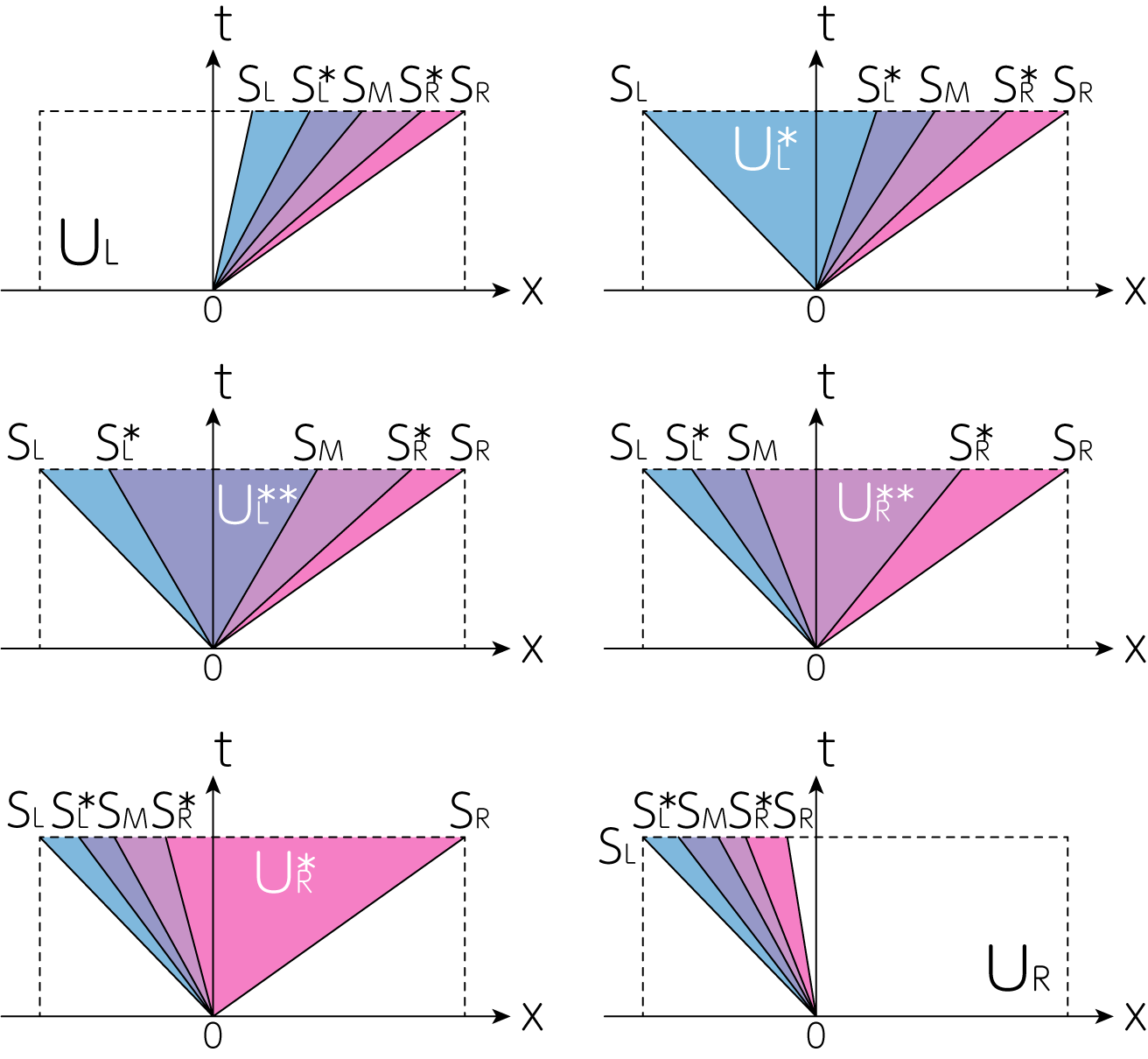
よって、数値計算を行う場合に、その流束の選択は
\[\mathbf{F}_\mathrm{HLLD} = \left\{ \begin{array}{ll} \mathbf{F}_L & \mathrm{if} \ S_L > 0 \\ \mathbf{F}_L^\ast & \mathrm{if} \ S_L \leq 0 < S_L^\ast \\ \mathbf{F}_L^{\ast \ast} & \mathrm{if} \ S_L^\ast \leq 0 < S_M \\ \mathbf{F}_R^{\ast \ast} & \mathrm{if} \ S_M \leq 0 < S_R^\ast \\ \mathbf{F}_R^\ast & \mathrm{if} \ S_R^\ast \leq 0 < S_R \\ \mathbf{F}_R & \mathrm{if} \ S_R \leq 0 \end{array}\right. \tag{32}\]HLLD流束の計算モジュール
以下にHLLD流束計算コードのJulia実装例を示します。
using LinearAlgebra
include("../convert/convert.jl")
include("../const/const.jl")
function hlld_core(rol, vnl, vtl, vul, prl, bnl, btl, bul, ror, vnr, vtr, vur, prr, bnr, btr, bur)
# compute B * B at left side
bl2 = dot([bnl, btl, bul], [bnl, btl, bul])
# compute fast-mode speed at left side
gmprl = gm * prl
vfl = sqrt(((bl2+gmprl)+sqrt((bl2+gmprl)^2-4*gmprl*bnl^2))/(2*rol))
# compute B * B at right side
br2 = dot([bnr, btr, bur], [bnr, btr, bur])
# compute fast-mode speed at right side
gmprr = gm * prr
vfr = sqrt(((br2+gmprr)+sqrt((br2+gmprr)^2-4*gmprr*bnr^2))/(2*ror))
# compute sl, sr
sl = min(vnl, vnr) - max(vfl, vfr)
sr = max(vnl, vnr) + max(vfl, vfr)
# compute bnc from HLL average
bnc = (sr*bnr-sl*bnl) / (sr-sl)
# compute pt at left and right sides
ptl = prl + 0.5 * bl2
ptr = prr + 0.5 * br2
# compute sm (=vn) at Riemann fan
slvnl = sl - vnl
srvnr = sr - vnr
rolslvnl = rol * slvnl
rorsrvnr = ror * srvnr
sm = (rorsrvnr*vnr-rolslvnl*vnl-ptr+ptl) / (rorsrvnr-rolslvnl)
# compute pt at riemann fan
pti = (rorsrvnr*ptl-rolslvnl*ptr+rolslvnl*rorsrvnr*(vnr-vnl)) / (rorsrvnr-rolslvnl)
# compute ro at outer sides in Riemann fan
slsm = sl - sm
roil = rol * slvnl / slsm
srsm = sr - sm
roir = ror * srvnr / srsm
# compute vy, vz, by, bz at left outer side in Riemann fan
smvnl = sm - vnl
if abs(rolslvnl*slsm-bnc^2) > 1.0e-10
denol = 1.0 / (rolslvnl*slsm-bnc^2)
vtil = vtl - btl * bnc * smvnl * denol
vuil = vul - bul * bnc * smvnl * denol
btil = btl * (rol*slvnl^2-bnc^2) * denol
buil = bul * (rol*slvnl^2-bnc^2) * denol
else
# if denominator == 0, substitute with vy, vz, by, bz at left state
vtil = vtl
vuil = vul
btil = btl
buil = bul
end
# compute vy, vz, by, bz at right outer side in Riemann fan
smvnr = sm - vnr
if abs(rorsrvnr*srsm-bnc^2) > 1.0e-10
denor = 1.0 / (rorsrvnr*srsm-bnc^2)
vtir = vtr - btr * bnc * smvnr * denor
vuir = vur - bur * bnc * smvnr * denor
btir = btr * (ror*srvnr^2-bnc^2) * denor
buir = bur * (ror*srvnr^2-bnc^2) * denor
else
# if denominator == 0, substitute with vy, vz, by, bz at right state
vtir = vtr
vuir = vur
btir = btr
buir = bur
end
# compute en at left state
vl2 = dot([vnl, vtl, vul], [vnl, vtl, vul])
enl = 0.5 * (rol*vl2+bl2) + prl * gm1i
# compute en at right state
vr2 = dot([vnr, vtr, vur], [vnr, vtr, vur])
enr = 0.5 * (ror*vr2+br2) + prr * gm1i
# compute en at left outer side in Riemann fan
vlbl = dot([vnl, vtl, vul], [bnl, btl, bul])
vilbil = dot([sm, vtil, vuil], [bnc, btil, buil])
enil = (slvnl*enl-ptl*vnl+pti*sm+bnc*(vlbl-vilbil)) / slsm
# compute en at right outer side in Riemann fan
vrbr = dot([vnr, vtr, vur], [bnr, btr, bur])
virbir = dot([sm, vtir, vuir], [bnc, btir, buir])
enir = (srvnr*enr-ptr*vnr+pti*sm+bnc*(vrbr-virbir)) / srsm
# compute ro at inner side in Riemann fan
roiil = roil
roiir = roir
# compute vy, vz, by, bz at inner side in Riemann fan
rtroil = sqrt(roil)
rtroir = sqrt(roir)
denoii = 1.0 / (rtroil+rtroir)
signbn = sign(bnc)
vtii = (rtroil*vtil+rtroir*vtir+(btir-btil)*signbn) * denoii
vuii = (rtroil*vuil+rtroir*vuir+(buir-buil)*signbn) * denoii
btii = (rtroil*btir+rtroir*btil+rtroil*rtroir*(vtir-vtil)*signbn) * denoii
buii = (rtroil*buir+rtroir*buil+rtroil*rtroir*(vuir-vuil)*signbn) * denoii
# compute en at left & right inner side in Riemann fan
viibii = dot([sm, vtii, vuii], [bnc, btii, buii])
eniil = enil - rtroil * (vilbil-viibii) * signbn
eniir = enir + rtroir * (virbir-viibii) * signbn
# choose flux
if sl > 0.0
result = [rol, vnl, vtl, vul, ptl, enl, bnc, btl, bul, vlbl]
elseif sl <= 0.0 < sm - abs(bnc) / rtroil
result = [roil, sm, vtil, vuil, pti, enil, bnc, btil, buil, vilbil]
elseif sm - abs(bnc) / rtroil <= 0.0 < sm
result = [roiil, sm, vtii, vuii, pti, eniil, bnc, btii, buii, viibii]
elseif sm <= 0.0 < sm + abs(bnc) / rtroir
result = [roiir, sm, vtii, vuii, pti, eniir, bnc, btii, buii, viibii]
elseif sm + abs(bnc) / rtroir <= 0.0 < sr
result = [roir, sm, vtir, vuir, pti, enir, bnc, btir, buir, virbir]
else
result = [ror, vnr, vtr, vur, ptr, enr, bnc, btr, bur, vrbr]
end
return result
end
function hlld!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64)
for i in 1:nxmax-1
# set primitive variables at left side
rol = Vl[1, i]
vnl = Vl[2, i]
vtl = Vl[3, i]
vul = Vl[4, i]
prl = Vl[5, i]
bnl = Vl[6, i]
btl = Vl[7, i]
bul = Vl[8, i]
# set primitive variables at right side
ror = Vr[1, i]
vnr = Vr[2, i]
vtr = Vr[3, i]
vur = Vr[4, i]
prr = Vr[5, i]
bnr = Vr[6, i]
btr = Vr[7, i]
bur = Vr[8, i]
# compute HLLD flux
result, tmp = hlld_core(rol, vnl, vtl, vul, prl, bnl, btl, bul, ror, vnr, vtr, vur, prr, bnr, btr, bur)
# convert flux and input to F
F[:, i] = Convert.i_to_f(result...)
end
end
HLLD計算サブルーチンは
- 準備部分
- コア計算部分 (hlld_core)
の2つに分かれています。これは多次元への拡張を容易にするためのものです。例えば2次元の理想磁気流体方程式を見てみましょう。
\[\frac{\partial}{\partial t} \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \\ B_x \\ B_y \\ B_z \end{array} \right) + \frac{\partial}{\partial x} \underbrace{\left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot} - B_x B_x \\ \rho v_y v_x - B_y B_x \\ \rho v_z v_x - B_z B_x \\ (E + P_\mathrm{tot}) v_x - (\mathbf{v} \cdot \mathbf{B}) B_x \\ 0 \\ B_y v_x - v_y B_x \\ B_z v_x - v_z B_x \\ \end{array}\right)}_{= \mathbf{F}} + \frac{\partial}{\partial y} \underbrace{\left( \begin{array}{c} \rho v_y \\ \rho v_x v_y - B_x B_y \\ \rho v_y v_y + P_\mathrm{tot} - B_y B_y \\ \rho v_z v_y - B_z B_y \\ (E + P_\mathrm{tot}) v_y - (\mathbf{v} \cdot \mathbf{B}) B_y \\ B_x v_y - v_x B_y \\ 0 \\ B_z v_y - v_z B_y \\ \end{array}\right)}_{=\mathbf{G}} = \mathbf{0} \tag{33}\]\(\mathbf{F}\)を計算する際に利用したサブルーチンにおいて\(v_x \rightarrow v_y, v_y \rightarrow v_z, v_z \rightarrow v_x, B_x \rightarrow B_y, B_y \rightarrow B_z, B_z \rightarrow B_x\)のように変換し、さらに\(F_2 \rightarrow F_3, F_3 \rightarrow F_4, F_4 \rightarrow F_2, F_6 \rightarrow F_7, F_7 \rightarrow F_8, F_8 \rightarrow F_6\)のように変換したものは\(G\)に一致します。このような回転対称性を用いることで、サブルーチンを再利用することが可能となります。 具体的には上述のhlld_coreでは、\(x\)方向の流束を計算するときには\(v_n = v_x, v_t = v_y, v_u = v_z\)などをインプットとし、\(y\)方向の流束の場合には\(v_n = v_y, v_t = v_z, v_u = v_x\)などをインプットにしており、hlld_core部分を変更することなく多次元計算にも用いることが可能です。
HLL, HLLC-G, HLLC-L, HLLDの4手法での、磁気流体衝撃波管問題を解いたときのガス密度分布を比較した図を以下に示します。
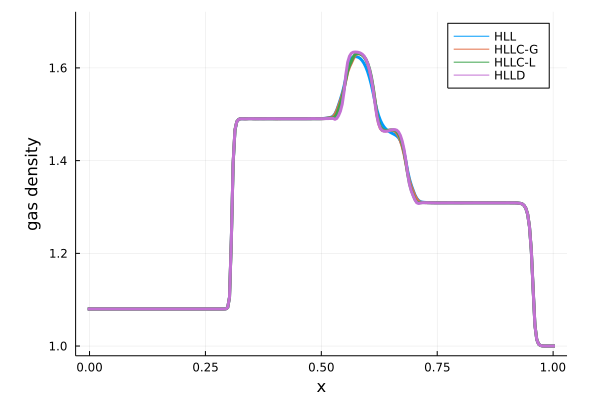
わかりくいため、さらに\(0.5 \leq x \leq 0.75\)の領域部分を拡大して描画したものを示します。
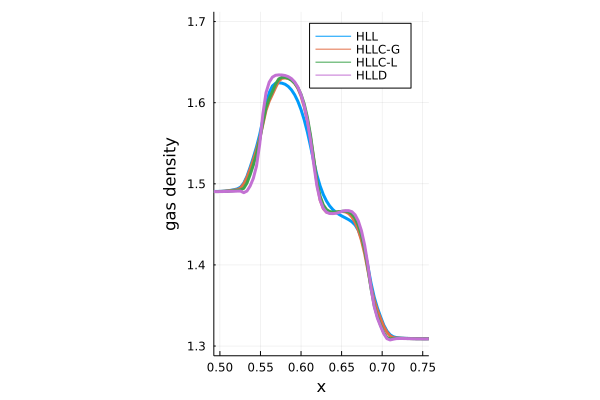
紫線のHLLD法は、\(x = 0.55\)の不連続面を一番正確に捉えられていることができます。さらに\(0.55 \leq x \leq 0.6\)に存在する密度ピークの最大値も、HLLD法が一番大きくなっています。 このことからわかるように、HLLD法は数値粘性の影響を一番抑えられていることがわかります。
色弱の方には見えにくい配色をしているかもしれない...申し訳ないです。
近いうちに配色の勉強もしたいかもしれない(2022年8月12日現在)
参考文献
- Miyoshi & Kusano, 2005, “A multi-state HLL approximate Riemann solver for ideal magnetohydrodynamics”
- Ryu & Jones, 1994, “Numerical Magnetohydrodynamics in Astrophysics: Algorithm and Tests for One-Dimensional Flow”
- Stone et al., 2008, “Athena: A New Code for Astrophysical MHD”
- Qiita記事, 磁気流体の数値計算で遊ぶ
- CANS+ドキュメント, 磁気流体力学方程式に対する近似リーマン解法