Table of contents

1. 宇宙を構成する物質の状態方程式
   1. 非相対論的物質(バリオン)の場合
   2. 非相対論的物質(ダークマター)の場合
   3. 相対論的物質(光子)の場合
      1. 補遺: 光子のエネルギー密度
      2. 補遺: 光子数密度
   4. 相対論的物質(ニュートリノ)の場合
   5. 宇宙膨張を加速させるもの(ダークエネルギー)の場合
   6. 空間(真空)の場合

宇宙を構成する物質の状態方程式

物質、もしくは相対論的粒子からなる輻射、そしてダークエネルギーが優勢かどうかを今後議論するために、これらの状態方程式を

$$p=w\rho c^2$$

という形で求め、その$w$の値を具体的に求めていくことを考えましょう。

非相対論的物質(バリオン)の場合

$$\frac{p_b}{{\rho }_b{c}^2}\simeq \frac{v^2}{c^2}\sim 0$$

より$w_b\sim 0$となります。

非相対論的物質(ダークマター)の場合

$$\frac{p_{\mathrm{D}\mathrm{M}}}{{\rho }_{\mathrm{D}\mathrm{M}}{c}^2}\simeq \frac{v^2}{c^2}\sim 0$$

より$w_{\mathrm{D}\mathrm{M}}\sim 0$となります。

相対論的物質(光子)の場合

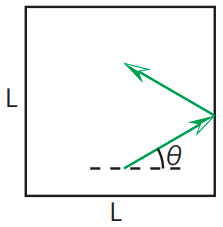
光子が一辺$L$の立方体に閉じ込められているとしましょう。図のように完全弾性衝突を考えると、1回の衝突で$x$方向の壁に与える力積は

$$\mathrm{\Delta }{p}_x=\frac{2h\nu }{c}\cos \theta$$

となります。$x$方向に一往復するのにかかる時間は$t=2L/(c\cos \theta )$より

$$\begin{array}{rl}{p}_{\gamma }& =\iint \frac{\frac{2h\nu }{c}\cos \theta }{t}\frac{L^3}{e^{h\nu /(k_{B}T)}-1}\frac{2{\nu }^2}{c^3}\frac{d\nu d\mathrm{\Omega }}{L^2}=\iint \frac{\frac{2h{\nu }^3}{c^3}{\cos }^2\theta }{e^{h\nu /(k_{B}T)}-1}d\nu d\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}d\nu {\int }_{-1}^{1}d\mu 2\pi \frac{\frac{2h{\nu }^3}{c^3}{\mu }^2}{e^{h\nu /(k_{B}T)}-1}\\ & =\frac{1}{3}\underset{{\rho }_{\gamma }{c}^2}{\underbrace{4\pi {\int }_0^{\mathrm{\infty }}d\nu \frac{\frac{2h{\nu }^3}{c^3}}{e^{h\nu /(k_{B}T)}-1}}}=\frac{1}{3}{\rho }_{\gamma }{c}^2\end{array}$$

よって$w_{\gamma }=\frac{1}{3}$です。

補遺: 光子のエネルギー密度

1辺$L$の立方体の中に光子が閉じ込められていることを考えます。光子が存在しているということは$L$で周期境界条件を満たしていると考えることができるので

$$e^{i\mathbf{k}\cdot \mathbf{x}}=e^{i{k}_{x}x+i{k}_{y}y+i{k}_{z}z}$$ $$\{\begin{array}{l}{k}_{x}L=2\pi n_x(n_x=0,\pm 1,\pm 2,\cdots )\\ k_{y}L=2\pi n_y\\ k_{z}L=2\pi n_z\end{array}$$

と書けます。よって状態数は

$$d{n}_{x}d{n}_{y}d{n}_z=\frac{d{k}_x}{2\pi /L}\frac{d{k}_y}{2\pi /L}\frac{d{k}_z}{2\pi /L}=\frac{L^3}{(2\pi {)}^3}d{k}_{x}d{k}_{y}d{k}_z$$

よって状態密度は

$$\frac{d^{3}n}{L^3}=\frac{d^3\mathbf{k}}{(2\pi {)}^3}=\frac{1}{(2\pi {)}^3}{k}^2\sin {\theta }_{k}dkd{\theta }_{k}d\phi \underset{k=2\pi \nu /c}{\underbrace{=}}\frac{{\nu }^2}{c^3}d\nu d\mathrm{\Omega }$$

途中、$\mathbf{k}$空間での極座標積分を考えて変形を行いました。統計力学の知識より、占有率は$e^{-ϵ/(k_{B}T)}$、光子はボーズ粒子より、カノニカル分布の分配関数は

$$Z=\sum _{n=0}^{\mathrm{\infty }}{e}^{-nh\nu /(k_{B}T)}\underset{\mathrm{無}\mathrm{限}\mathrm{等}\mathrm{比}\mathrm{級}\mathrm{数}\mathrm{の}\mathrm{和}}{\underbrace{=}}\frac{1}{1-e^{-h\nu /(k_{B}T)}}$$

$x=h\nu /(k_{B}T)$と置換して、エネルギー$ϵ=nh\nu$の光子の平均個数を導出しましょう。

$$f_{\gamma }(\nu )=\sum _{n=0}^{\mathrm{\infty }}n\frac{e^{-nx}}{Z}=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{Z}(-\frac{d{e}^{-nx}}{dx})=-\frac{1}{Z}\frac{dZ}{dx}=\frac{1}{e^x-1}$$

よってエネルギー密度${\rho }_{\gamma }{c}^2$は、(光子1個のエネルギー)$\times$(平均個数)$\times$状態密度$\times$独立モード数2を積分したものです。

$${\rho }_{\gamma }{c}^2={\int }_0^{\mathrm{\infty }}d\nu {\int }_0^{4\pi }\frac{2{\nu }^2}{c^3}\frac{h\nu }{e^{h\nu /(k_{B}T)}-1}d\nu d\mathrm{\Omega }$$

となります。ついでにさらに計算を行うと

$${\rho }_{\gamma }{c}^2=\frac{8\pi }{c^3}\frac{k_B^4{T}^4}{h^3}\underset{=6\zeta (4)={\pi }^4/15}{\underbrace{{\int }_0^{\mathrm{\infty }}\frac{x^3}{e^x-1}dx}}=\frac{8{\pi }^5{k}_B^4}{15c^3{h}^3}{T}^4$$

補遺: 光子数密度

$$n={\int }_0^{\mathrm{\infty }}d\nu {\int }_0^{4\pi }d\mathrm{\Omega }\frac{1}{e^{h\nu /(k_{B}T)}-1}\frac{2{\nu }^2}{c^3}=\frac{8\pi }{c^3}\frac{k_B^3{T}^3}{h^3}\underset{=2\zeta (3)\sim 2.4}{\underbrace{{\int }_0^{\mathrm{\infty }}\frac{x^2}{e^x-1}dx}}$$

CMB(宇宙マイクロ波背景放射)は現在の宇宙で$T\simeq 2.725$Kより、$n_{\gamma ,0}\sim 412{\mathrm{c}\mathrm{m}}^{-3}$となります。

相対論的物質(ニュートリノ)の場合

統計力学の知識より、占有率は$e^{-ϵ/(k_{B}T)}$、ニュートリノはフェルミオンより、カノニカル分布分配関数は

$$Z=\sum _{n=0}^1{e}^{-nh\nu /(k_{B}T)}=1+e^{-h\nu /(k_{B}T)}$$

ここでニュートリノは質量0を仮定します。この仮定により光子と同様の計算で平均個数・状態密度を求めることができます。

$$f_{\mathrm{F}\mathrm{D}}(\nu )=\frac{1}{Z}{e}^{-h\nu /(k_{B}T)}=\frac{1}{1+e^{h\nu /(k_{B}T)}}$$

よってエネルギー密度${\rho }_{\gamma }{c}^2$は、(ニュートリノ1個のエネルギー)$\times$(平均個数)$\times$状態密度$\times$独立モード数1を積分したものです。

$${\rho }_{\nu }{c}^2={\int }_0^{\mathrm{\infty }}d\nu {\int }_0^{4\pi }d\mathrm{\Omega }\frac{h\nu }{e^{h\nu /k_{B}T}+1}\frac{2{\nu }^2}{c^3}=\frac{8\pi }{c^3}\frac{k_B^4{T}^4}{h^3}{\int }_0^{\mathrm{\infty }}\frac{x^3}{e^x+1}dx$$ $$\frac{1}{e^{2x}-1}=\frac{1}{(e^x+1)(e^x-1)}=\frac{1}{2}(\frac{1}{e^x-1}-\frac{1}{e^x+1})⟹\frac{1}{e^x+1}=\frac{1}{e^x-1}-\frac{2}{e^{2x}-1}$$

より

$${\int }_0^{\mathrm{\infty }}\frac{x^3}{e^x+1}dx={\int }_0^{\mathrm{\infty }}(\frac{x^3}{e^x-1}-\frac{2x^3}{e^{2x}-1})dx={\int }_0^{\mathrm{\infty }}\frac{x^3}{e^x-1}dx-\frac{1}{8}{\int }_0^{\mathrm{\infty }}\frac{X^3}{e^X-1}dX=\frac{7}{8}{\int }_0^{\mathrm{\infty }}\frac{x^3}{e^x-1}dx$$

これらより

$$p_{\nu }=\frac{1}{3}{\rho }_{\nu }{c}^2,{\rho }_{\nu }{c}^2=\frac{7}{8}{\rho }_{\gamma }{c}^2$$

よって$w_{\nu }=\frac{1}{3}$です。
ちなみに

$$T_{\nu }={\left(\frac{4}{11}\right)}^{1/3}{T}_{\mathrm{C}\mathrm{M}\mathrm{B}}\sim 1.95[\mathrm{K}],n_{\nu }\sim 112[{\mathrm{c}\mathrm{m}}^{-3}]$$

です。

宇宙膨張を加速させるもの(ダークエネルギー)の場合

フリードマン方程式より

$$\frac{\ddot{a}}{a}=-\frac{4\pi G}{3}({\rho }_{\mathrm{D}\mathrm{E}}+\frac{3p_{\mathrm{D}\mathrm{E}}}{c^2})=-\frac{4\pi G}{3}{\rho }_{\mathrm{D}\mathrm{E}}(1+3w_{\mathrm{D}\mathrm{E}})$$

加速膨張では$\ddot{a}>0$より$w_{\mathrm{D}\mathrm{E}}<-\frac{1}{3}$となります。

空間(真空)の場合

空間は宇宙に膨張も収縮ももたらさないとすると、フリードマン方程式より

$$1+3w_K=0⟹w_K=-\frac{1}{3}$$

です。