sinc関数の積分
複素数平面状で経路積分を行うことによりsinc関数の\([-\infty, \infty]\)の積分
\[\int_{-\infty}^\infty \frac{\sin x}{x} \ dx= \pi\]を求めましょう。
複素積分
\[f(z) = \frac{e^{iz}}{z} \ \ (z = x + iy)\]を以下のような閉曲線上で積分することを考えます。
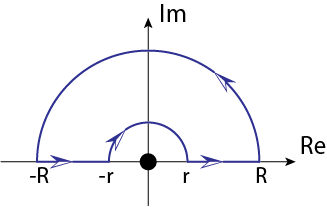
\(f(z)\)は閉曲線の内部で常に正則なので、コーシーの積分定理より
\[\oint_{C_1 +C_2 +C_3 +C_4} f(z) \ dz = 0\]\(C_2\)上において\(z=Re^{i\theta}\)より\(dz=iRe^{i\theta} d\theta\)
\[\int_{C_2} f(z) \ dz = \int^{\pi}_{0} i R e^{i\theta} \frac{e^{iR e^{i\theta}}}{R e^{i\theta}} \ d \theta = i \int^{\pi}_{0} e^{iR \cos \theta} e^{-R \sin \theta} \ d\theta\]\(C_4\)上の積分も同様に
\[\int_{C_4} f(z) \ dz = \int^{0}_{\pi} i r e^{i\theta} \frac{e^{ir e^{i\theta}}}{r e^{i\theta}} \ d \theta = i \int^{0}_{\pi} e^{ir \cos \theta} e^{-r \sin \theta} \ d\theta\] \[\therefore \ \int_{r}^{R} \frac{e^{ix}}{x} \ dx + \int_{-R}^{-r} \frac{e^{ix}}{x} \ dx + i \left( \int_{0}^\pi e^{iR\cos \theta} e^{-R \sin \theta} \ d\theta+ \int_\pi^0 e^{ir \cos \theta} e^{-r \sin \theta} \ d\theta \right) = 0\]ここで
\[\lim_{R \rightarrow \infty} \left| \int_0^\pi e^{iR \cos \theta} e^{-R\sin \theta} \ d \theta \right| \le \lim_{R \rightarrow \infty} \int_0^\pi \underbrace { \left| e^{iR \cos \theta} \right| }_{=1} \left|e^{-R\sin \theta} \right| d \theta = 0\] \[\lim_{r \rightarrow 0} \int_\pi^0 e^{ir \cos \theta} e^{-r \sin \theta} \ d \theta = \int_\pi^0 d \theta = - \pi\] \[\therefore \ \int_0^{\infty} \frac{e^{ix}}{x} \ dx + \int_{- \infty}^0 \frac{e^{ix}}{x} \ dx- i\pi = 0\]第2項において\(x=-X\)のように置換することで整理ができるので
\[\therefore \ \int_0^{\infty} \frac{e^{ix} - e^{- ix}}{x} \ dx = 2i \int_0^{\infty} \frac{\sin x}{x} \ dx \underbrace{=}_{偶関数より} i \int_{-\infty}^{\infty} \frac{\sin x}{x} \ dx = i\pi \ \Longrightarrow \int_{-\infty}^\infty \frac{\sin x}{x} \ dx = \pi\]結言
複素関数を用いることで、ある値に積分が収束することを示しました。この積分は特にディリクレ積分という名前がついており、有名です。