Table of contents
磁気流体における誘導方程式
導出
まずは用いる基礎方程式を準備します。Maxwell方程式のFaradayの法則より
\[\frac{1}{c} \frac{\partial \mathbf{B}}{\partial t} = - \nabla \times \mathbf{E} \tag{1}\]変位電流を無視したAmpereの法則より
\[\nabla \times \mathbf{B} = \frac{4\pi}{c} \mathbf{j} \tag{2}\]Ohmの法則より
\[\mathbf{j} = \sigma \left( \mathbf{E} + \mathbf{v} \times \frac{\mathbf{B}}{c}\right) \tag{3}\]これらを用いると
\[\frac{\partial \mathbf{B}}{\partial t} = - c \nabla \times \left( \frac{\mathbf{j}}{\sigma} - \mathbf{v} \times \frac{\mathbf{B}}{c} \right) = \nabla \times (\mathbf{v} \times \mathbf{B}) - \nabla (\eta \nabla \times \mathbf{B})\]ここで\(\eta \equiv c^2 / (4\pi \sigma)\)のように置きました。これが定数であると仮定すると、第2項は
\[\begin{aligned} \{ \nabla \times (\nabla \times \mathbf{B}) \}_i &= \epsilon_{ijk} \partial_j \{ \nabla \times \mathbf{B} \}_k = \epsilon_{ijk} \partial_j (\epsilon_{k \ell m} \partial_\ell B_m) = \epsilon_{kij} \epsilon_{k \ell m} \partial_j \partial_\ell B_m = (\delta_{i\ell} \delta_{jm} - \delta_{im} \delta_{j\ell}) \partial_j \partial_\ell B_m \\ &= \partial_j \partial_i B_j - \partial_j \partial_j B_i = \partial_i \underbrace{(\nabla \cdot \mathbf{B})}_{=0} - \nabla^2 B_i \end{aligned}\]のように計算されるので、最終的に
\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) + \eta \nabla^2 \mathbf{B} \tag{4}\]となります。これを誘導方程式(induction equation)と呼びます。左辺が時間1階微分なのに対して、右辺第2項は空間2階微分です。よってこの項は拡散を表しており、\(\eta\)を磁気拡散係数(magnetic diffusivity)と呼びます。
磁気レイノルズ数
(4)式の第1項と第2項のどちらが支配的かを大雑把に見積もってみましょう。空間微分を\(\nabla \simeq L^{-1}\)のように典型的な空間スケールの逆数として考えると
\[\frac{| \nabla \times (\mathbf{v} \times \mathbf{B})| }{|\eta \nabla^2 \mathbf{B}|} \simeq \frac{L V}{\eta}\]のようになります。\(\eta\)が大きいとき、もしくは空間スケールや流体の典型的な速度が小さいとき、磁気拡散もその系を支配する物理過程となることがわかります。\(R_m \equiv LV/\eta\)を磁気Reynolds数と呼びます。
磁束凍結定理
\(R_m \gg 1\)として、拡散が無視できる理想的な場合を考えてみましょう(\(\eta \propto \sigma^{-1}\)より、電気伝導度が無限大の極限、すなわちperfectly conducting limitと考えることができます)。この状況下で流体中のある面を貫く磁場の量、すなわち磁束\(\Phi\)について考えます。定義より
\[\Phi = \iint_S \mathbf{B} \cdot d \mathbf{S} \tag{5}\]このLagrange微分を考えましょう。すると、これは面\(S\)と一緒に運動するような観測者が感じる\(\Phi\)の時間変化を調べることになります。このとき、この時間変化には
- 磁場そのものが時間とともに変化する効果
- 流れによって面\(S\)が移動・変形する効果
の2つが存在するはずです。1つ目の効果については\(\frac{\partial \mathbf{B}}{\partial t}\)です。効果2については面\(S\)を囲む閉曲線を\(C\)、その微小線素ベクトルを\(d\mathbf{s}\)とします。すると流体速度が\(\mathbf{v}\)のとき、微小時間\(dt\)の間に\(d\mathbf{s}\)が\(\mathbf{v} dt\)だけ動いたとすれば、それによる面積の変化は\(d\mathbf{S} = \mathbf{v} dt \times d \mathbf{s}\)のようになります。
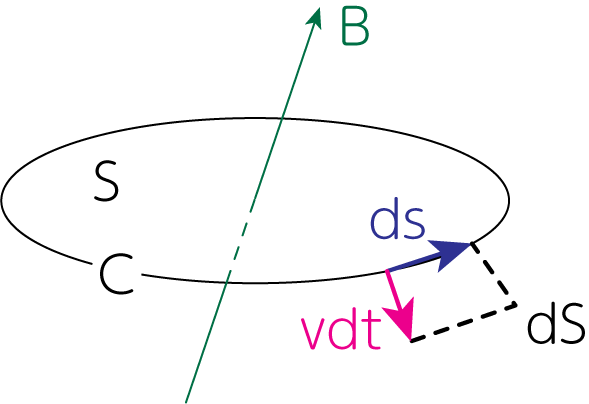
よって面積\(d\mathbf{S}\)を貫く磁場の量は
\[\mathbf{B} \cdot d \mathbf{S} = \mathbf{B} \cdot (\mathbf{v} dt \times d \mathbf{s}) = - dt (\mathbf{v} \times \mathbf{B}) \cdot d\mathbf{s} \tag{6}\]以上から
\[\frac{D \Phi}{Dt} = \iint_S \frac{\partial \mathbf{B}}{\partial t} \cdot d \mathbf{S} - \oint_C \mathbf{v} \times \mathbf{B} \cdot d\mathbf{s} = \iint_S \left\{ \frac{\partial \mathbf{B}}{\partial t} - \nabla \times (\mathbf{v} \times \mathbf{B}) \right\} \cdot d \mathbf{S} \underbrace{=}_{(4)} 0\]のように磁束が流体の流れに沿って保存さていることがわかります。途中、Stokesの回転定理を用いました。
磁束だけではなく、今度は磁力線一本について考えてみましょう。それにはまず\(\mathbf{B}/\rho\)(単位質量あたりの磁場、specific mean magnetic field)のLagrange微分を計算します。
ここで
\[\begin{aligned} \{ \nabla \times (\mathbf{v} \times \mathbf{B}) \}_i &= \epsilon_{ijk} \epsilon_{k \ell m} \partial_j v_\ell B_m = (\delta_{i \ell} \delta_{jm} - \delta_{im} \delta_{j \ell}) \partial_j v_\ell B_m = \partial_j (v_i B_j) - \partial_j (v_j B_i) \\ &= B_j \partial_j v_i + v_i \partial_j B_j - B_i \partial_j v_j - v_j \partial_j B_i = \{ (\mathbf{B} \cdot \nabla) \mathbf{v} + \underbrace{(\nabla \cdot \mathbf{B})}_{=0} \mathbf{v} - (\nabla \cdot \mathbf{v}) \mathbf{B} - (\mathbf{v} \cdot \nabla) \mathbf{B} \}_i \end{aligned}\]より
\[\frac{D}{Dt} \left( \frac{\mathbf{B}}{\rho} \right) = \frac{\mathbf{B}}{\rho} (\nabla \cdot \mathbf{v}) + \frac{1}{\rho} \{ (\mathbf{B} \cdot \nabla) \mathbf{v} - \mathbf{B} (\nabla \cdot \mathbf{v})\} = \left( \frac{\mathbf{B}}{\rho} \cdot \nabla \right) \mathbf{v} \tag{7}\]のように書かれます。
次にこれとの比較として、時刻\(t\)で位置\(\mathbf{x}(t), \mathbf{x}(t) + \delta \mathbf{x}(t)\)にあった2つの流体要素が時刻\(t+\delta t\)にそれぞれ\(\mathbf{x}(t+\delta t), x(t+\delta t) + \delta \mathbf{x} (t+\delta t)\)に移動したとしましょう。流体の速度を\(\mathbf{v}(\mathbf{x}, t)\)とすると
の2つより
\[\delta \mathbf{x}(t + \delta t) \simeq \delta \mathbf{x}(t) + (\delta \mathbf{x} \cdot \nabla) \mathbf{v} \delta t \ \Longrightarrow \ \frac{D \delta \mathbf{x}}{Dt} = (\delta \mathbf{x} \cdot \nabla) \mathbf{v} \tag{8}\]となります。最後の式で\(\delta t \rightarrow 0\)の極限がLagrange微分となるのは、今考えているのが流体要素の運動だからです。
(7), (8)式を見比べてみると、式の形が全く同じであることがわかります。つまり、\(\delta \mathbf{x} \parallel \mathbf{B}\)となるように選べば、その後もこの2つのベクトルは常に平行を維持します。これは微小な距離だけ離れた2つの流体要素が同じ磁力線上にあるとすると、その2つの流体要素はその後も同じ磁力線上に存在することを意味します。これを磁力線の凍結(frozen-in)と呼びます。

このことから、流体の運動が磁力線に変形をもたらすため、(4)式の\(\nabla \times (\mathbf{v} \times \mathbf{B})\)のことを対流項と呼ぶこともあります。
数値計算しやすい形に変形
\(\nabla \times (\mathbf{v} \times \mathbf{B})\)の形では見通しが悪いので、運動量保存則と同様の形に整えましょう。
\[\nabla \times (\mathbf{v} \times \mathbf{B}) = \epsilon_{ijk} \partial_j \epsilon_{k\ell m} v_\ell B_m \mathbf{e}_i = \epsilon_{kij} \epsilon_{k \ell m} \partial_j (v_\ell B_m) \mathbf{e}_i = (\delta_{i\ell} \delta_{jm} - \delta_{im} \delta_{j\ell}) \partial_j (v_\ell B_m) \mathbf{e}_i = \partial_j (v_i B_j - B_i v_j) \mathbf{e}_i = \nabla \cdot (\mathbf{v} \mathbf{B} - \mathbf{B} \mathbf{v})\]より
\[\frac{\partial \mathbf{B}}{\partial t} + \nabla \cdot (\mathbf{B} \mathbf{v} - \mathbf{v} \mathbf{B}) = \mathbf{0} \tag{9}\]のようになります。