輻射駆動風 (radiatively driven wind)
太陽風の場合は、輻射場の圧力はガス圧に比べて無視できましたが、早期型星では輻射場の効果によって恒星風が発生します。 圧力をガス圧\(P_\mathrm{gas}\)と輻射圧\(P_\mathrm{rad}\)に分け、定常球対称風に対する運動方程式を書くと
\[v \frac{dv}{dr} = -\frac{1}{\rho} \frac{dP_\mathrm{gas}}{dr} - \frac{1}{\rho} \frac{dP_\mathrm{rad}}{dr} - \frac{GM_r}{r^2} \tag{1}\]のようになります。 輻射圧は光子による運動量の輸送ですが、恒星内部のような光学的に厚く輻射に対して拡散近似が使える場合には、簡単な表現式が使えます。 最初に光学的に厚い場合を考え、その後に一般的な場合を考えましょう。
光学的に厚い場合
恒星内部のような光学的に厚い状態では、輻射圧は温度だけの関数となり
\[P_\mathrm{rad} = \frac{1}{3} a_\mathrm{R} T^4 \tag{2}\]と書けます。 ここで\(a_\mathrm{R}\)は輻射定数 (radiation constant)を表します。 また
\[\frac{L_\mathrm{rad}}{4\pi r^2} = - \frac{4a_\mathrm{R} c}{3\kappa \rho} T^3 \frac{dT}{dr} = - \frac{c}{\kappa \rho} \frac{dP_\mathrm{rad}}{dr} \tag{3}\]という関係があります。 さらに
\[\begin{align} \frac{dP_\mathrm{gas}}{dr} &= \frac{d}{dr} \left( \frac{\rho}{\mu m_p} k_B T\right) = \frac{k_B T}{\mu m_p} T \frac{d\rho}{dr} + \frac{\rho}{\mu m_p} k_B \frac{dT}{dr} = a^2 \frac{d\rho}{dr} + P_\mathrm{gas} \frac{d\ln T}{dr} \notag \\ &= a^2 \frac{d\rho}{dr} + \frac{P_\mathrm{gas}}{4 P_\mathrm{rad}} \frac{dP_\mathrm{rad}}{dr} \tag{4} \end{align}\]という関係も成り立ちます。 ここで\(a^2 = \frac{k_B T}{\mu m_p}\)は等温の場合の音速です。 これらの関係を運動方程式(1)に代入すると
\[\begin{align} v \frac{dv}{dr} &= - \frac{a^2}{\rho} \frac{d\rho}{dr} + \frac{P_\mathrm{gas}}{P_\mathrm{rad}} \frac{\kappa}{4c} \frac{L_\mathrm{rad}}{4\pi r^2} + \frac{\kappa L_\mathrm{rad}}{4\pi c r^2} - \frac{GM_r}{r^2} = - \frac{a^2}{\rho} \frac{d\rho}{dr} + \frac{\kappa L_\mathrm{rad}}{4\pi c r^2} \left( 1 + \frac{P_\mathrm{gas}}{P_\mathrm{rad}}\right) - \frac{GM_r}{r^2} \notag \\ &= - \frac{a^2}{\rho} \frac{d\rho}{dr} - \frac{GM_r}{r^2} (1-\Gamma_\mathrm{rad}) \tag{5} \end{align}\]が得られます。 ここで\(\Gamma_\mathrm{rad}\)は、輻射力と重力の比で
\[\Gamma_\mathrm{rad} \equiv \frac{\kappa L_\mathrm{rad}}{4\pi c r^2} \left( 1 + \frac{P_\mathrm{gas}}{P_\mathrm{rad}}\right) \frac{r^2}{GM_r} = \frac{\kappa L_\mathrm{rad}}{4\pi c GM_r} \frac{P}{P_\mathrm{rad}} = \frac{\kappa L_\mathrm{rad}}{4\pi c GM_r (1-\beta)} \tag{6}\]のように定義されます。 また\(\beta\)はガス圧と全圧との比で
\[\beta \equiv \frac{P_\mathrm{gas}}{P}, \quad \frac{P_\mathrm{rad}}{P} = \frac{P - P_\mathrm{gas}}{P} = 1 - \beta \tag{7}\]という関係があります。
\(\frac{d\rho}{dr} < 0\)とすると、加速が起こるための必要条件は
となります。 これはエディントン限界の電子散乱不透明度の場所に、\(\kappa\)を入れたものです。 光度の高い星では密度が低いため、内部のほとんどの領域で不透明度は電子散乱不透明度に近い値を持ちます。 そのため、このような加速が起こるためにはエディントン限界に近い光度を持つような恒星で起こりやすくなります (水素やヘリウムの電離領域では不透明度は大きな値を持ちますが、そこでは対流が発生しており、密度が比較的大きい場所では対流の効率が良いため \(L_\mathrm{rad} \ll L_r\)となっています。 また密度が小さく対流の効率の悪い場所では、density inversionの存在で\(\frac{d\rho}{dr} >0\)となっており、加速の起きにくい環境となっています。) 新星爆発の途中で起こる質量放出は、光学的に厚い領域での加速が主に働いて起こっています。
等温のコロナ風の場合との比較のため、質量保存の式\(\dot{M} = 4\pi r^2 \rho v\)を用いて\(\frac{d\rho}{dr}\)を消去しましょう。
より
\[\begin{align} &v \frac{dv}{dr} = \frac{a^2}{\rho} \frac{1}{rv} \left( 2 \rho v + r \rho \frac{dv}{dr}\right) - \frac{GM_r}{r^2} (1-\Gamma_\mathrm{rad}) = \frac{2a^2}{r} + \frac{a^2}{v^2} v \frac{dv}{dr} - \frac{GM_r}{r^2} (1-\Gamma_\mathrm{rad}) \notag \\ & \Longrightarrow \ \left( 1 - \frac{a^2}{v^2}\right) v \frac{dv}{dr} = \frac{2a^2}{r} - \frac{GM_r}{r^2} (1-\Gamma_\mathrm{rad}) \tag{10} \end{align}\]が得られます。 等温のコロナ風の場合との違いは、重力に\(1-\Gamma_\mathrm{rad}\)の因子がかかっている点です。 光学的に厚い場合、輻射の力は重力を小さくしたのとほぼ同等の効果を持つことがわかります。 この恒星風を含む構造を計算するには、上述の運動方程式をエネルギー保存の式
\[T v \frac{dS}{dr} = \epsilon_\mathrm{n} - \frac{1}{4\pi r^2 \rho} \frac{dL_r}{dr} \tag{11}\]そして温度勾配と\(L_r\)との関係式などを連立させて解く必要があります。
光学的に薄い場合
ここでは、輻射に対して拡散近似が使えない場合を考えましょう。 このような状況は恒星太樹の領域で実現されるため、以下では\(M_r = M, L_r = L_\mathrm{rad} = L\)とします。
輻射圧は光子による運動量輸送であるため、天頂角\(\theta\)方向の輻射強度を\(I_\nu (r, \theta)\)とすると
のように表されます。 ここで\(\Omega\)は立体角を表します。 この式を\(r\)で微分すると
\[\frac{dP_\mathrm{rad}}{dr} = \frac{1}{c} \int_0^\infty d\nu \int_{4\pi} d\Omega \frac{\partial I_\nu (r, \theta)}{\partial r} \cos^2 \theta \tag{13}\]となります。 この式に現れた\(\frac{\partial I_\nu}{\partial r}\)に、輻射輸送の式
\[\cos \theta \frac{\partial I_\nu}{\partial r} = - (\kappa_\nu + \sigma_\mathrm{e}) \rho I_\nu + \eta_\nu \rho + \frac{\sigma_\mathrm{e}}{4\pi} \int_{\Omega'} p(\theta, \varphi; \theta', \varphi') I_\nu(\theta', \varphi') d\Omega' \tag{14}\]を用いましょう。 ここで\(\kappa_\nu, \sigma_\mathrm{e}, \eta_\nu\)はそれぞれ単位質量あたりの吸収係数、電子散乱断面積、発光係数を表し、さらに\(p(\theta, \varphi; \theta', \varphi')\)は\((\theta', \varphi')\)方向から\((\theta, \varphi)\)方向への散乱確率を表します。 この式に\(\cos \theta\)をかけ、立体角\(\Omega\)で積分すると
\[\int_{4\pi} \cos^2 \theta \frac{\partial I_\nu}{\partial r} d\Omega = - (\kappa_\nu + \sigma_\mathrm{e}) \rho \int_{4\pi} I_\nu \cos \theta d\Omega \equiv - (\kappa_\nu + \sigma_\mathrm{e}) \rho F_\nu \tag{15}\]が得られます。 ここで\(F_\nu\)は、振動数\(\nu\)の光の単位振動数あたりの流束(フラックス)を表します。 この式を振動数について積分すると、その左辺は\(\frac{dP_\mathrm{rad}}{dr}\)に比例します。 すなわち
\[\frac{dP_\mathrm{rad}}{dr} = - \frac{\rho}{c} \int_0^\infty (\kappa_\nu + \sigma_\mathrm{e}) F_\nu d\nu = - \frac{\sigma_\mathrm{e} \rho L}{4\pi cr^2} - \frac{\rho}{c} \int_0^\infty \kappa_\nu F_\nu d\nu \tag{16}\]という関係が成り立ちます。 ここで、電子散乱断面積 \(\sigma_\mathrm{e}\)が振動数に依存しないことを用いました。
この式を運動方程式(1)に代入すると
が得られます。 ここで\(\Gamma_\mathrm{e}, \Gamma_\kappa\)は
\[\Gamma_\mathrm{e} \equiv \frac{\sigma_\mathrm{e} L}{4\pi c GM}, \quad \Gamma_\kappa \equiv \frac{r^2}{c GM} \int_0^\infty \kappa_\nu F_\nu d\nu \tag{18}\]のように定義されます。 この\(\Gamma_\mathrm{e}, \Gamma_\kappa\)はそれぞれ、電子散乱および吸収によりガスが輻射から受ける外向きの力と重力の比を表しています。 これらの効果により、恒星風が起こる可能性を示しています。
吸収線による加速
早期型星では密度が小さいため、不透明度は電子散乱不透明度に近づいています。 したがって、\(\Gamma_\kappa\)は線吸収の寄与によるものが多くなります。 この吸収線の効果を考慮する方法は、Castor et al. (1975)により考え出され、現在でも早期型星の恒星風計算にはこれが用いられています。
1つのスペクトル線による寄与\(\Gamma_{\kappa \ell}\)は
のように近似できます。 ここで\(\Delta \nu_\ell\)は吸収線幅を表し、添字の\(\nu \ell\)は吸収線の振動数を意味します。 この量を評価するためには、恒星風内での\(F_\nu\)を知る必要があります。
光球から出た連続フラックス\(F_\mathrm{c} (\nu)\)は、光学的厚み\(\tau_\nu\)を通過すると吸収を受け
のようになります。 恒星風内のイオンは、このように減衰を受けたフラックスを受けるため、\(\Gamma_{\kappa \ell}\)の平均値 \(\langle \Gamma_{\kappa \ell} \rangle\)は
\[\langle \Gamma_{\kappa \ell} \rangle \tau_{\nu \ell} \propto \Delta \nu_\ell \kappa_{\nu \ell} \int_0^{\tau_{\nu \ell}} e^{-\tau} d\tau = \Delta \nu_\ell \kappa_{\nu \ell} (1-e^{-\tau_{\nu \ell}}) \tag{21}\] \[\langle \Gamma_{\kappa \ell} \rangle \propto \Delta \nu_\ell \kappa_{\nu \ell} \frac{(1-e^{-\tau_{\nu \ell}})}{\tau_{\nu \ell}} \simeq \Delta \nu_\ell \kappa_{\nu \ell} \min ( 1, 1/\tau_{\nu \ell}) \tag{22}\]のように得られます。 \(\min (1, 1/\tau_{\nu \ell})\)の1は光学的に薄い場合に対応し、\(1/\tau_{\nu \ell}\)は光学的に厚い場合に対応します。
静的な環境のもとでは\(\tau_\nu = \int_R^\infty \kappa_\nu \rho dr\)のように計算されます。 しかし恒星風内のように速度場が存在する場合、ある場所であるイオンが吸収する吸収線の振動数でのフラックスは、その速度場に起因するドップラー効果により
の間しか吸収を受けなくなります。 これをソボレフ近似 (Sobolev approximation)と呼びます。 ここで\(v_\mathrm{th}\)はイオンの熱速度を表します。
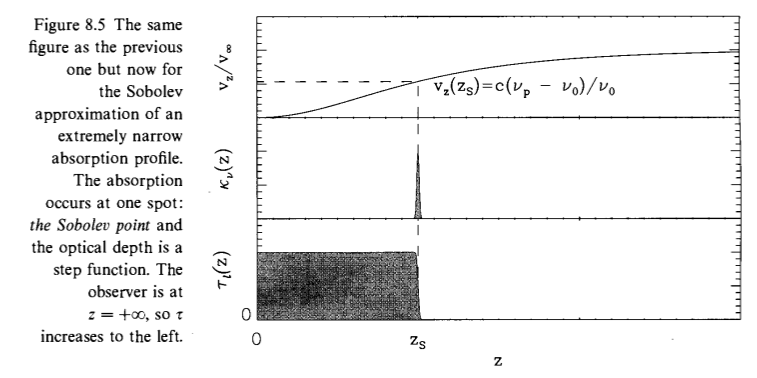
introduction to Stellar Windsより
そして、それに対応する光学的深さ
\[\tau_{\nu \ell} = \kappa_{\nu \ell} \rho \Delta r \approx \frac{v_\mathrm{th} \kappa_{\nu \ell} \rho }{\left\vert \frac{dv}{dr} \right\vert} \tag{24}\]のようになります。 \(\dot{M} = 4\pi r^2 \rho v\)から\(\rho\)を消去すると
\[\frac{1}{\tau_{\nu \ell}} = \frac{4\pi}{\dot{M} v_\mathrm{th} \kappa_{\nu \ell}} r^2 v \frac{dv}{dr} = \frac{4\pi}{\dot{M} v_\mathrm{th} \sigma_\mathrm{e}} \left( r^2 v \frac{dv}{dr} \right) \frac{\sigma_\mathrm{e}}{\kappa_{\nu \ell}} \tag{25}\]となります。 これらの関係を用いると、1つの吸収線からの寄与 \(\Gamma_{\kappa \ell}\)が得られます。 種々の吸収線の効果を加えることにより、吸収線全体の効果 \(\Gamma_\kappa\)が得られます。 この量は
\[\Gamma_\kappa = \sum_\mathrm{lines} \Gamma_{\kappa \ell} = \Gamma_\mathrm{e} \sum_\mathrm{lines} \frac{\kappa_{\nu \ell}}{\sigma_\mathrm{e}} \Delta \nu_ell \min(1, 1/\tau_{\nu \ell}) \equiv \Gamma_\mathrm{e} \mathcal{M} \tag{26}\]のように表され、すべての吸収線加速の効果はradiation-force multiplier (輻射力乗数？)と呼ばれる\(\mathcal{M}\)に集約されます。 これは近似的に
\[\mathcal{M} = k \left( \frac{4\pi}{\sigma_\mathrm{e} v_\mathrm{th} \dot{M}}\right)^\alpha \left( r^2 v \frac{dv}{dr}\right)^\alpha = k t^\alpha \tag{27}\]と表されます。 \(\alpha\)は、光学的に薄い吸収線のみ集めたとするとゼロとなり、逆に光学的に厚い吸収線のみを集めたとすると1になるような量です。 実際は、光学的に厚い吸収線と薄い吸収線の両方が寄与するため、\(0 \leq \alpha \leq 1\)となります。 数十万本の吸収線を考慮した最近の計算では、\(k \sim 0.5 - 1, \alpha \sim 0.5\)です。
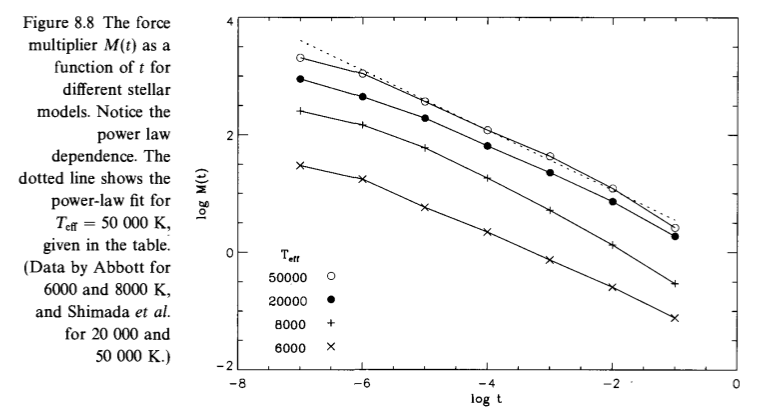introduction to Stellar Windsより
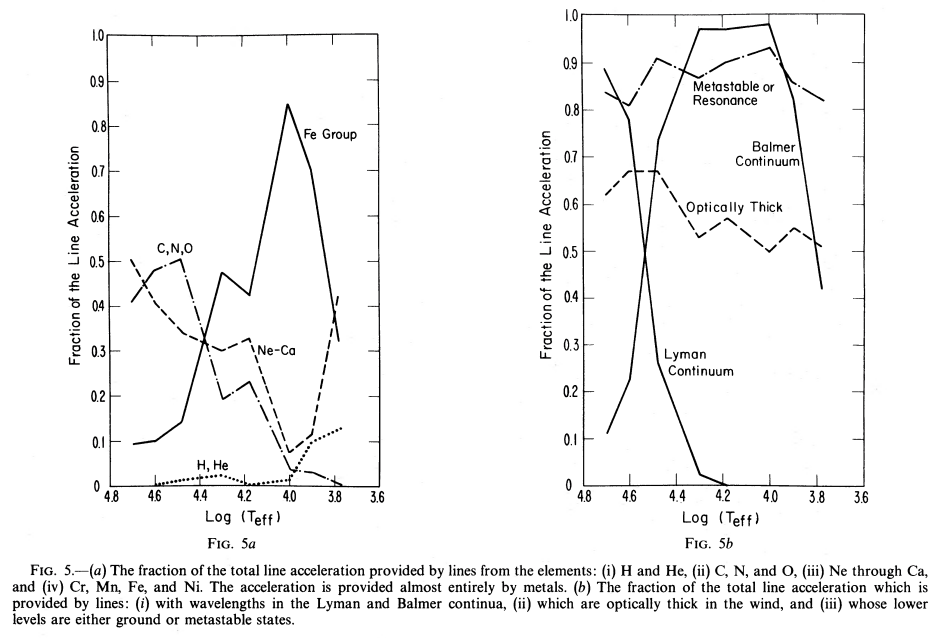
どのイオンが重要であるかは、恒星の表面温度によって異なり、それは熱速度と脱出速度との比に影響を及ぼすようです。 その比は、数万度以上の高温の星では\(\sim 2.6\)で一定ですが、比較的低温の星ではより小さい比となります。 表面温度が数万度以上の星では、C, N, OおよびNe, Caが重要な役割を果たします。
特異点
式を簡単な形に書くために、スペクトル線による効果\(\Gamma_\kappa\)を
\[GM \Gamma_\kappa = C \left( r^2 v \frac{dv}{dr} \right)^\alpha \qquad \left( C \equiv k \Gamma_\mathrm{e} \left( \frac{4\pi}{\sigma_\mathrm{e} v_\mathrm{th} \dot{M}}\right)^\alpha GM \right) \tag{28}\]のように表すことにしましょう。 すると運動方程式(17)は
\[r^2 v \frac{dv}{dr} = - \frac{r^2}{\rho} \frac{dP_\mathrm{gas}}{dr} - GM (1-\Gamma_\mathrm{e}) + C \left( r^2 v \frac{dv}{dr} \right)^\alpha \tag{29}\]と書けます。 \(C\)は\(\dot{M}\)を含み、固有値として求めることができます。 簡単のため、等温を仮定すると
\[\frac{dP_\mathrm{gas}}{dr} = \frac{P_\mathrm{gas}}{\rho} \frac{d\rho}{dr} = \frac{a^2 \dot{M}}{4\pi} \frac{d}{dr} \left( \frac{1}{vr^2} \right) = -a^2 \rho \left( \frac{1}{v} \frac{dv}{dr} + \frac{2}{r} \right) \qquad (a^2 \equiv P_\mathrm{gas} / \rho) \tag{30}\]となります。 これを運動方程式に代入すると
\[\left( 1 - \frac{a^2}{v^2}\right) r^2 v \frac{dv}{dr} = 2a^2 r - GM(1-\Gamma_\mathrm{e}) + C \left( r^2 v \frac{dv}{dr}\right)^\alpha \tag{31}\]を得ます。 さらに\(y \equiv r^2 v \frac{dv}{dr}\)を定義すると、運動方程式は
\[F(r, v, y) = 2a^2 r - GM(1-\Gamma_\mathrm{e}) + Cy^2\alpha - \left( 1 - \frac{a^2}{v^2}\right) y = 0 \tag{32}\]と表されます。 この式は常に成り立たなければならないため、その変分もゼロで
\[\delta F = \frac{\partial F}{\partial r} \delta r + \frac{\partial F}{\partial v} \delta v + \frac{\partial F}{\partial y} \delta y = 0 \tag{33}\]なので
\[\frac{dy}{dr} = - \frac{\frac{\partial F}{\partial r} + \frac{\partial F}{\partial v} \frac{d v}{d r}}{\frac{\partial F}{\partial y}} \tag{34}\]のように書けます。 (32)式より\(\frac{\partial F}{\partial y}\)は
\[\frac{\partial F}{\partial y} = \alpha C y^{\alpha -1} - \left( 1-\frac{a^2}{v^2}\right) \tag{35}\]と計算できます。 星の表面付近では、\(v \ll a\)であるため、\(\frac{\partial F}{\partial y} > 0\)であるのに対し、十分遠方では\(v \gg a\)であるとともに吸収線の効果は小さくなるため\(\frac{\partial F}{\partial y}<0\)となっています。 したがって\(\frac{\partial F}{\partial y}=0\)となる場所が存在します。 そこでは運動方程式が singular (regular singularity)となっています。 特異点での量に添字\(c\)をつけて表すと、\(\frac{\partial F}{\partial y} = 0\)より
\[\alpha C y_c^{\alpha - 1} = 1 - \frac{a^2}{v_c^2} \tag{36}\]が得られます。 この関係を特異点での運動方程式に代入すると
\[\begin{align} &2a^2 r_c - GM (1-\Gamma_\mathrm{e}) + \frac{1}{\alpha} \left( 1 - \frac{a^2}{v_c^2}\right) y_c - \left( 1 - \frac{a^2}{v_c^2}\right) y_c = 0 \notag \\ &\Longrightarrow \ y_c = \frac{\alpha}{1-\alpha} \frac{GM(1-\Gamma_\mathrm{e}) - 2a^2 r_c}{1 - \frac{a^2}{v_c^2}} \tag{37} \end{align}\]が得られます。 また特異点でも\(\frac{dy}{dr}\)は有限であるべきなので
\[\left( \frac{\partial F}{\partial r} + \frac{\partial F}{\partial v} \frac{dv}{dr}\right)_c = 0 \tag{38}\]が成り立ちます。 この式から\(r_c, v_c\)との関係を得ることができます。 以上から、\(C, y_c, r_c\)を\(v_c\)の関数として表すことができました。
解析解
超音速領域では\(v^2 \gg a^2\)、さらに
\[2GM (1- \Gamma_\mathrm{e}) = R_\ast v_\mathrm{esc}^2 \gg R_\ast a^2 \simeq r_c a^2 \tag{39}\]なので、運動方程式で音速が現れる項は微小として無視することができます。
\[F(r, v, y) = - GM(1-\Gamma_\mathrm{e}) + Cy^\alpha - y = 0 \tag{40}\]となります。 これは\(y\)が定数であることを示しているため
\[y(r) = r^2 v \frac{dv}{dr} = y_c = \frac{\alpha}{1-\alpha} GM(1-\Gamma_\mathrm{e}) = \frac{1}{2} \frac{\alpha}{1-\alpha} R_\ast v_\mathrm{esc}^2 \ \Longrightarrow \ \frac{dv^2}{dr} = \frac{\alpha}{1-\alpha} \frac{R_\ast v_\mathrm{esc}^2}{r^2} \tag{41}\]が得られます。 音速点\(r_s\)から\(r\)まで積分すると
\[v^2 = a^2 + \frac{\alpha}{1-\alpha} R_\ast v_\mathrm{esc}^2 \left( \frac{1}{r_s} - \frac{1}{r} \right) \simeq \frac{\alpha}{1-\alpha} v_\mathrm{esc}^2 \left( 1- \frac{R_\ast}{r} \right) \tag{42}\]が得られます。 一番最後の関係を得るのに、\(v^2 \gg a^2, r_s \sim R_\ast\)を用いました。 この式に\(r \rightarrow \infty\)を代入すれば
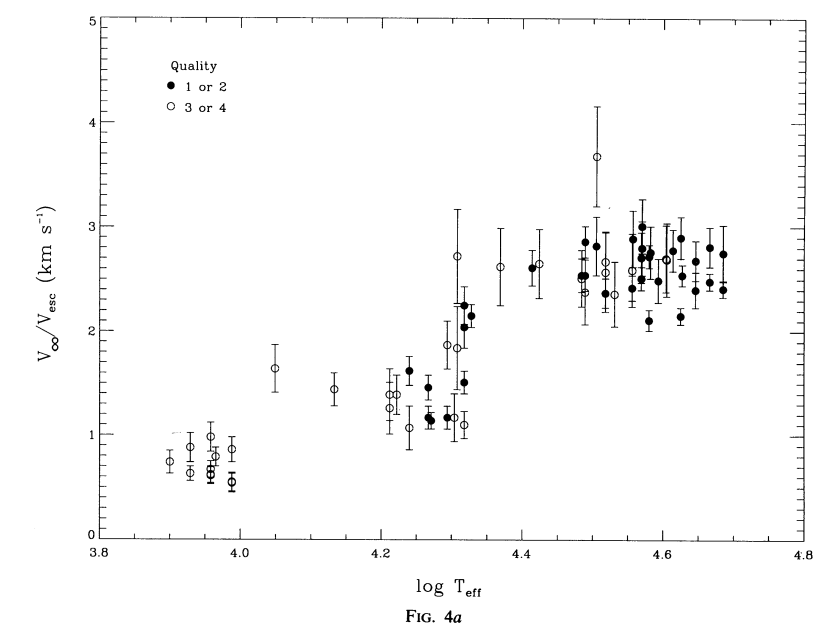
\[v_\infty^2 = \frac{\alpha}{1-\alpha} v_\mathrm{esc}^2 \tag{43}\]という関係が得られます。 これは終端速度が脱出速度に比例することを表し、次の図の\(T_\mathrm{eff} > 2 \times 10^4 \mathrm{K}\)で終端速度と脱出速度の比が一定になっていることに対応します。
またこの関係をもとの式に用いると
\[v(r) \simeq v_\infty \left( 1 - \frac{R_\ast}{r}\right)^{0.5} \tag{44}\]が得られます。 これは\(\beta\)-lawの\(\beta=0.5\)となっています。 また、この近似の範囲では
\[C \equiv GM k \Gamma_\mathrm{e} \left(\frac{4\pi}{\sigma_\mathrm{e} v_\mathrm{th} \dot{M}}\right)^\alpha = \frac{y_c^{1-\alpha}}{\alpha} = \frac{\left\{ \frac{\alpha}{1-\alpha} GM (1-\Gamma_\mathrm{e})\right\}^{1-\alpha} }{\alpha} \tag{45}\]の関係から、\(\dot{M}\)の関係を求めることができ
\[\dot{M} \propto L^{1/\alpha} M^{-(1-\alpha) / \alpha} \tag{46}\]となっていることがわかります。 この関係は、高温の大質量星に対する観測と一致します。
参考文献
[1] Abbott, 1982, “The theory of radiatively driven stellar winds. II. The line acceleration”
[2] Lamers et al., 1995, Terminal Velocities and the Bistability of Stellar Winds
[3] Lamers & Cassinelli, “Introduction to Stellar Winds”
[4] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”