Table of contents
X線バースター
小質量X線連星では、中性子星の周りに降着円盤ができます。 降着ガスは重力エネルギーを開放しながら円盤に沿って流れ込みます。 解放された重力エネルギーは、熱に変換され、円盤の表面から黒体放射として放出されます。 円盤は中性子星の表面近くまで延び、中性子星に近づくにつれてその温度が高くなります。 円盤中を中性子星表面スレスレまで降着してきたガスは、最初持っていた重力エネルギーの半分を黒体放射として解放しています。 最後に表面に落下すると、残りの半分の重力エネルギーが解放され、星表面の降着ガスは一気に加熱されます。 そして黒体放射でX線を放出するようになります。 小質量X線連星のスペクトルは、中性子星表面と円盤表面殻の黒体放射の重ね合わせとして説明することができます。
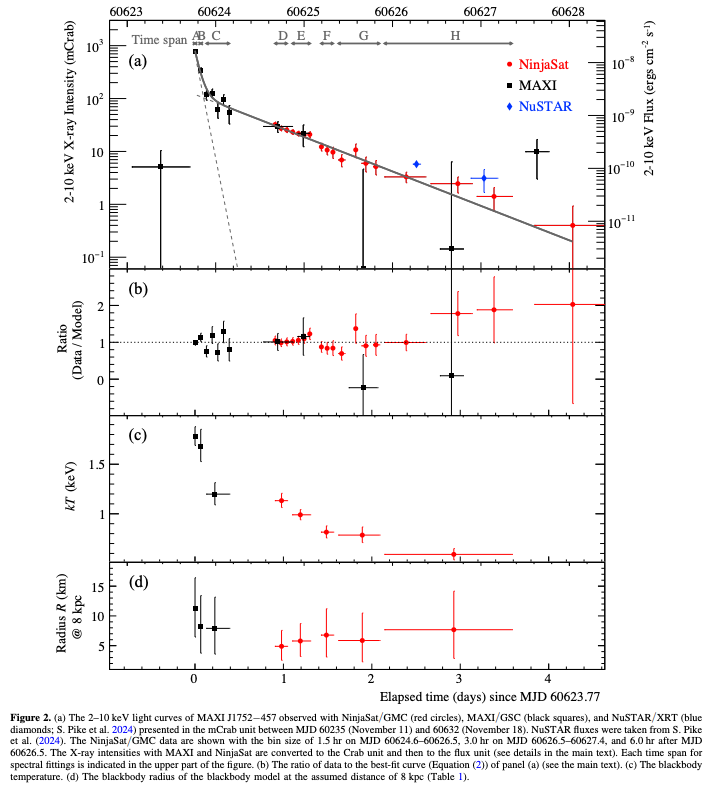
しかし、中性子星の小質量X線連星に特有な現象に、X線バーストと呼ばれるものがあります。 X線バーストとは、1秒程度の間にX線光度が急激に上昇し、その後数十秒かけてもとのX線高度に戻るような現象です。
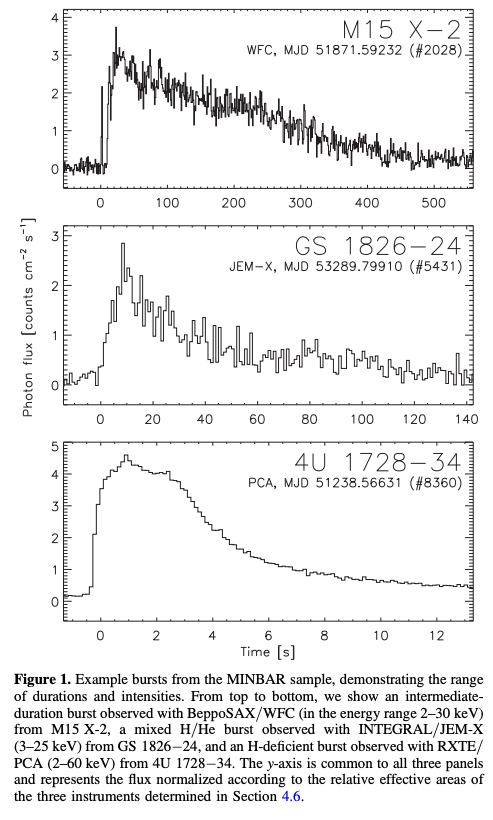
Galloway et al. (2020)より。横軸は秒単位の時間、縦軸は異なる装置で検出された光子フラックスを表す。
このX線バーストは、1969年に初観測され、その結果は Belian et al. (1972) として公開されました。 このようなX線バーストを起こすX線連星を、X線バースター (X-ray burster)と呼びます。 X線バースターとなる中性子星は、それほど強い磁場を持たないとされています。 強い磁場を持つ場合、降着流は磁力線に沿って磁極領域に流れ込むため、先ほどの説明とは異なる降着の形態を取るためです。
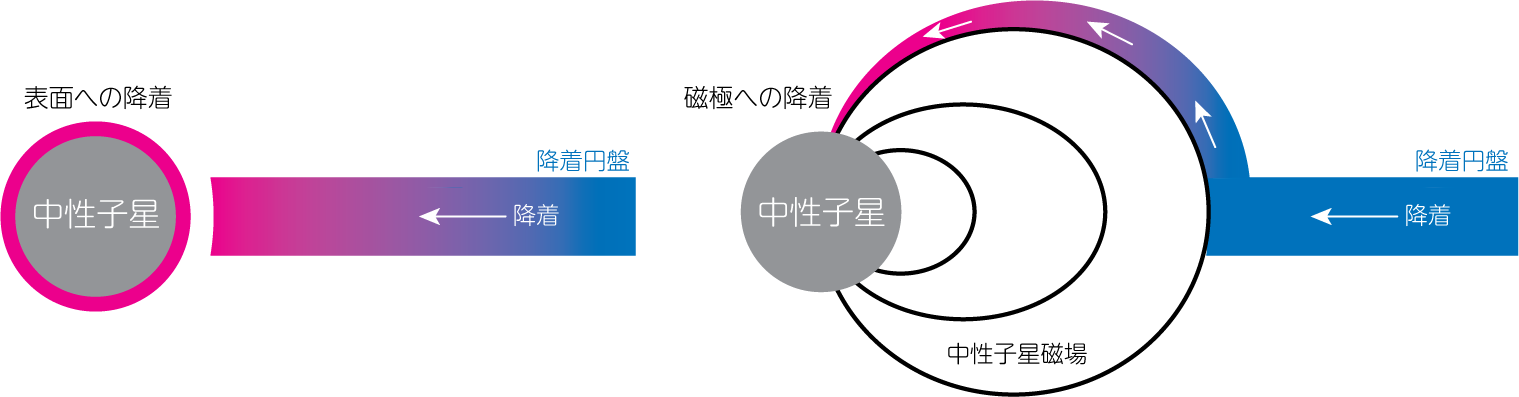
それぞれ弱磁場の中性子星への降着と、強磁場の中性子星への降着の様子。
中性子星への降着により物質が降り積り、ある臨界温度を超えると、バーストが起こります。 このメカニズムから分かるように、バースト発生後、再び降着によりガスが中性子星表面に降り積もると、再びバーストを起こすことができます。 典型的なX線バーストの間隔は、数時間から1日程度とされています。 X線バーストは、I型のII型の2種類に分類されます。 I型は、中性子星表面に降着した物質の不安定な核融合燃焼によるものとされています。 II型は、降着円盤から中性子星への散発的な質量降着が原因と考えられていますが、まだ2例しか発見されていません。
ここでは主に、I型のX線バースターについて議論していきましょう。
I型のX線バースターの観測的特徴など
I型X線バースターでは、X線はバースト成分と長く持続する成分として観測されます。 またX線バーストは繰り返し起こり、その発生間隔は数時間から数日程度まで及びます。 さらに一定期間X線バーストは観測されず、長く持続する成分のみが観測される場合もあり、その間はX線バースターは単にずっとX線を放射するX線源として観測されます。 バースト時に放出されるエネルギー量の時間平均と、持続成分のエネルギー量の時間平均の比を定義しましょう。 すなわち
\[\alpha \equiv \frac{\int_0^T L_X (\mathrm{burst}) dt / T}{\int_0^T L_X (\mathrm{persistene}) dt/T} \approx \frac{L_X (\mathrm{burst}) \Delta t_\mathrm{burst}}{L_X (\mathrm{persistent}) \Delta t_\mathrm{persistent}} \tag{1}\]です。 ここで\(T\)は観測時間、\(\Delta t_\mathrm{burst}\)と\(\Delta t_\mathrm{persistent}\)はそれぞれX線バーストと継続的なX線の時間です。 観測的には
\[\frac{L_X (\mathrm{burst})}{L_X (\mathrm{persistent})} \sim 10, \quad \frac{\Delta t_\mathrm{burst}}{\Delta t_\mathrm{persistent}} \sim 10^{-3} \tag{2}\]と判明しています。 よって\(\alpha \sim 10^{-2}\)と求まります。
ここで
としましょう。 ここで\(L_\mathrm{nuc}\)は核融合反応による光度、\(L_\mathrm{acc}\)は重力エネルギーの解放による光度です。 すると
\[\frac{\int_0^T L_X (\mathrm{burst}) dt}{\int_0^T L_X (\mathrm{persistent}) dt} \simeq \frac{L_\mathrm{nuc}}{L_\mathrm{acc}} \simeq \frac{0.007\dot{M} c^2}{\frac{GM\dot{M}}{R}} = \frac{0.007 c^2}{\frac{GM}{R}} \tag{4}\]のようになります。 途中、核融合反応によるエネルギー放出を、水素からヘリウムが生成するときの質量欠損分としました。 中性子星の場合、典型的な値は\(M \sim M_\odot, R\sim 10^6 \mathrm{cm}\)なので
\[\frac{\int_0^T L_X (\mathrm{burst}) dt}{\int_0^T L_X (\mathrm{persistent}) dt} \simeq \frac{2 \times 0.007R}{\frac{2GM}{c^2}} \simeq \frac{0.014 \times 10^6}{3 \times 10^5} \sim 0.04 \tag{5}\]と求まります。 途中、太陽質量のシュバルツシルト半径\(r_g = \frac{2GM}{c^2} \sim 3 \mathrm{km}\)であることを用いました。 最終的に求まった値は、観測で求まっている\(\alpha \sim 0.01\)と同じ程度になっています。
核燃焼殻の熱的不安定性
平衡状態
中性子星表面に降り注いだガスの薄い層が、核融合燃焼を起こした場合の安定性を議論しましょう。 降着した質量が形成した薄い層の厚さ\(\Delta r\)は、中性子星半径に比べて十分薄いとしましょう。 すると、質量降着層は平行平板層として扱うことができます。 一般相対論による効果を無視すると、静水圧平衡を表す式\(\frac{dP}{dr} = - \rho g\)から
\[P \approx \frac{\Delta M}{4\pi R^2 \Delta r} g \Delta r \approx \frac{\Delta M}{4\pi R^2} \frac{GM}{R^2} = \sigma g_s \tag{6}\]のようになります。 ここで中性子星表面での重力と柱密度を
\[g_s = \frac{GM}{R^2}, \quad \sigma = \rho \Delta r = \frac{\Delta M}{4\pi R^2} \tag{7}\]のようにしました。 (7)式から、圧力\(P\)は\(\sigma\)に線形に依存する程度で、ほぼ一定であることがわかります。 そして今の設定では、エネルギー保存の方程式は
\[C_P \frac{dT}{dt} \approx \epsilon - \epsilon_\mathrm{rad} \tag{8}\]のように簡単化することができます。 さらに
\[T \frac{ds}{dt} = T C_P \left( \frac{d \ln T}{dt} - \nabla_\mathrm{ad} \frac{d \ln P}{dt}\right) \approx C_P \frac{dT}{dt} \tag{9}\]のように近似しましょう。 これは断熱膨張による冷却効果を無視したことに対応します。 そして
\[\nabla \cdot \mathbf{F} = \nabla \cdot \left( - \frac{16 \sigma_\mathrm{SB} T^3}{3\kappa \rho} \nabla T\right) \approx \frac{4ac T^4}{3\kappa \rho \Delta r^2} = \rho \epsilon_\mathrm{rad} \tag{10}\]のようにしましょう。 途中、\(4\sigma_\mathrm{SB} = ac\)であり、\(a\)は放射定数です。 ここから
\[\epsilon_\mathrm{rad} = \frac{4ac T^4}{3\kappa \rho^2 \Delta r^2} = \frac{4ac T^4}{3\kappa \sigma^2} \tag{11}\]のようになります。
摂動を加えたときの安定性解析
熱的な安定性を調べるために、温度に次のような擾乱が加わったとしましょう。
\[T(t) = T_0 + \delta T (t) \tag{12}\]ここで\(T_0\)は摂動がない状態での温度、そして\(\delta T\)は温度の摂動を表します。 (8)式より
\[C_P \frac{d}{dt}(T_0 + \delta T) = C_P \frac{d \delta T}{dt} \approx \epsilon (T_0 + \delta T) - \epsilon_\mathrm{rad} (T_0 + \delta T) \tag{13}\]\(\epsilon, \epsilon_\mathrm{rad}\)も線形化しましょう。
\[\epsilon (T_0 + \delta T) \approx \epsilon (T_0) + \left. \frac{\partial \epsilon}{\partial T} \right|_{T_0} \delta T \tag{14}\] \[\epsilon_\mathrm{rad} (T_0 + \delta T) \approx \epsilon_\mathrm{rad} (T_0) + \left. \frac{\partial \epsilon_\mathrm{rad}}{\partial T} \right|_{T_0} \delta T \tag{15}\]平衡状態では\(C_P \frac{dT_0}{dt} = \epsilon(T_0) - \epsilon_\mathrm{rad} (T_0) =0\)より
\[C_P \frac{d \delta T}{dt} \approx \left. \left( \frac{\partial \epsilon}{\partial T} - \frac{\partial \epsilon_\mathrm{rad}}{\partial T}\right) \right|_{T_0} \delta T \ \Longrightarrow \ C_P \frac{d}{dt} \left( \frac{\delta T}{T_0}\right) = F \frac{\delta T}{T_0} \tag{16}\]ここで
\[F = \frac{1}{C_P T_0} \left. \left( \frac{\partial \epsilon}{\partial T} - \frac{\partial \epsilon_\mathrm{rad}}{\partial T}\right) \right|_{T_0} \tag{17}\]です。 これをもう少し具体的に整理していきましょう。 \(\epsilon\)(核融合反応による項)を計算していきましょう。 圧力が平衡状態のままの一定に保たれている場合、密度も変化するため
\[\left. \frac{\partial \epsilon}{\partial T} \right|_P = \left. \frac{\partial \epsilon}{\partial T} \right|_\rho + \left. \frac{\partial \epsilon}{\partial \rho} \right|_T \left. \frac{\partial \rho}{\partial T} \right|_\rho \tag{19}\]のような連鎖律となります。 両辺を対数微分にすると
\[\left. \frac{\partial \ln \epsilon}{\partial \ln T} \right|_P = \left. \frac{\partial \ln \epsilon}{\partial \ln T} \right|_\rho + \left. \frac{\partial \ln \epsilon}{\partial \ln \rho} \right|_T \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P = \epsilon_T + \epsilon_\rho \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \tag{20}\]のようになります。 途中
\[\epsilon_T \equiv \left. \frac{\partial \ln \epsilon}{\partial \ln T} \right|_\rho, \quad \epsilon_\rho \equiv \left. \frac{\partial \ln \epsilon}{\partial \ln \rho} \right|_T \tag{21}\]としました。 同様に、放射エネルギー損失(11)式の温度依存性から
\[\left. \frac{\partial \epsilon_\mathrm{rad}}{\partial T} \right|_P = \left. \frac{\partial \epsilon_\mathrm{rad}}{\partial T} \right|_\rho + \left. \frac{\partial \epsilon_\mathrm{rad}}{\partial \rho} \right|_T \left. \frac{\partial \rho}{\partial T} \right|_P \tag{22}\]となります。 両辺を対数微分にすると
\[\begin{align} \left. \frac{\partial \ln \epsilon_\mathrm{rad}}{\partial \ln T} \right|_P &= \left. \frac{\partial \ln \epsilon_\mathrm{rad}}{\partial \ln T} \right|_\rho + \left. \frac{\partial \ln \epsilon_\mathrm{rad}}{\partial \ln \rho} \right|_T \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \notag \\ &= \left. \frac{\partial}{\partial \ln T} (\ln T^4 - \ln \kappa - \ln \rho^2) \right|_\rho + \left. \frac{\partial}{\partial \ln \rho} (\ln T^4 - \ln \kappa - \ln \rho^2) \right|_T \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \notag \\ &= 4 - \left. \frac{\partial \ln \kappa }{\partial \ln T} \right|_\rho - \left( \left. \frac{\partial \ln \kappa}{\partial \ln \rho} \right|_T + 2\right) \left. \frac{\partial \ln \rho }{\partial \ln T} \right|_P = 4 - \kappa_T - (\kappa_\rho + 2) \left. \frac{\partial \ln \rho }{\partial \ln T} \right|_P \tag{23} \end{align}\]となります。 先程と同様に、途中
\[\kappa_T \equiv \left. \frac{\partial \ln \kappa }{\partial \ln T} \right|_\rho, \quad \kappa_\rho \equiv \left. \frac{\partial \ln \kappa}{\partial \ln \rho} \right|_T \tag{24}\]のように置きました。 以上を用いて(17)式を整理しましょう。
\[\begin{align} F &= \frac{1}{C_P T_0^2} \left. \left( \epsilon \frac{T}{\epsilon} \frac{\partial \epsilon}{\partial T} - \epsilon_\mathrm{rad} \frac{T}{\epsilon_\mathrm{rad}} \frac{\partial \epsilon_\mathrm{rad}}{\partial T}\right) \right|_{T_0} = \frac{1}{C_P T_0^2} \left. \left( \epsilon \frac{\partial \ln \epsilon}{\partial \ln T} - \epsilon_\mathrm{rad} \frac{\partial \ln \epsilon_\mathrm{rad}}{\partial \ln T}\right) \right|_{T_0} \notag \\ &= \frac{\epsilon_\mathrm{rad}}{C_P T_0^2} \left. \left( \frac{\epsilon}{\epsilon_\mathrm{rad}} \frac{\partial \ln \epsilon}{\partial \ln T} - \frac{\partial \ln \epsilon_\mathrm{rad}}{\partial \ln T}\right) \right|_{T_0} \notag \\ &= \frac{\epsilon_\mathrm{rad}}{C_P T_0^2} \left\{ \frac{\epsilon}{\epsilon_\mathrm{rad}} \left( \epsilon_T + \epsilon_\rho \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \right) - 4 + \kappa_T + (\kappa_\rho + 2) \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \right\} \notag \\ &= \frac{\epsilon_\mathrm{rad}}{C_P T_0^2} \left\{ \frac{\epsilon}{\epsilon_\mathrm{rad}} \epsilon_T - 4 + \kappa_T + \left( \frac{\epsilon}{\epsilon_\mathrm{rad}} \epsilon_\rho + \kappa_\rho + 2 \right) \left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P \right\} \tag{25} \end{align}\]本来は(25)式の+2がいらないらしい...計算ミス?結果としては同じような振る舞いとなるからまぁヨシ(๑˃̵ᴗ˂̵)و
不安定となる条件は?
(16)式から
\[\frac{\delta T}{T_0} \propto \exp \left( Ft/ C_P\right) \tag{26}\]のようになります。 \(F>0\)の場合、摂動温度が指数関数的に増大することがわかります。 そこで(25)式から、現実的な場合に\(F>0\)となるかどうかを調べてみましょう。 中性子星表面に降着したガスが、理想気体であるとすると
\[P = \frac{\rho k_B T}{\mu m_p} \ \Longrightarrow \ \ln P = \ln \rho + \ln T \ \Longrightarrow \ d \ln P = d\ln \rho + d\ln T \tag{27}\]のようになります。 圧力が一定の場合
\[\left. \frac{\partial \ln \rho}{\partial \ln T} \right|_P = -1 \tag{28}\]となることがわかります。 さらに現実的な場合においては
\[\epsilon_\rho \sim 1, \quad \kappa_\rho \sim 1, \quad \kappa_T \sim 0, \quad \epsilon \simeq \epsilon_\mathrm{rad} \tag{29}\]が良い近似として成り立ちます。 すると(25)式は
\[F \approx \frac{\epsilon_\mathrm{rad}}{C_P T_0^2} (\epsilon_T - 8 ) \tag{30}\]となります。 以上から\(\epsilon_T \gg 1\)であるなら、温度が指数的に増加し、不安定であるとわかります。
例えば、トリプルアルファ反応によるヘリウム生成過程で発生するエネルギーは
です。 ここで\(\rho_2 = \rho / 10^2 \mathrm{g}, T_8 = T/10^8 \mathrm{K}\)、そして\(Y\)はヘリウム組成比です。 ここから、ヘリウム燃焼温度である\(T_8 \sim 1\)では
\[\epsilon_T \approx -3 + \frac{44.04}{T_8} \sim 41 \tag{32}\]のようになり、ヘリウム燃焼は中性子星表面の薄い殻部分では強く不安定であることがわかります。 これにより質量が降り積もった中性子星表面で核燃焼が暴走し、X線バーストが発生します。
CNOサイクルによる水素燃焼の場合
です。 ここで\(T_6 = T / 10^6 \mathrm{K}\)です。 \(T_6 \sim 10\)の場合
\[\epsilon_T \approx - \frac{2}{3} + \frac{50.76}{T_6^{1/3}} \sim 23 \tag{34}\]のように値が求まります。 これは、水素燃焼も同様に不安定であることがわかります。 しかし\(T \gtrsim 10^8 \mathrm{K}\)の高温でのCNO燃焼の場合、エネルギー発生率は\(\epsilon \approx 5.8 \times 10^{15} Z_\mathrm{CNO} [\mathrm{erg/g/s}]\)のように温度にほぼ依存しない形となります。 以上から、\(\frac{\partial \epsilon}{\partial T} \sim 0\)となり、水素燃焼が安定に起こることがわかります。
質量降着率とX線バーストの関係
ここまで見てきたように、温度によってX線バーストを引き起こす核燃焼が異なることがわかります。 伴星から中性子星に降着する物質においてヘリウム組成比が大きくなると、表面で起こる薄い殻におけるヘリウム燃焼は不安定となり、これがX線バーストを引き起こします。 この不安定性は質量降着率にも依存します。 質量降着率とX線バーストにおける種類の関係を、以下の表にまとめました。
| 降着率 | 核燃焼のタイプ |
|---|---|
| \(\dot{M}/(M_\odot \mathrm{yr}^{-1}) > 2.6 \times 10^{-8}\) | 水素とヘリウムの混合した層内で、安定して水素とヘリウム核燃焼が起こる |
| \(2.6 \times 10^{-8} > \dot{M}/(M_\odot \mathrm{yr}^{-1}) > 10^{-9}\) | 水素とヘリウムの混合した層内で、熱的に不安定なヘリウムフラッシュが起こる |
| \(10^{-9} > \dot{M}/(M_\odot \mathrm{yr}^{-1}) > 2 \times 10^{-10}\) | 水素燃焼が安定に燃えたのち、生成物であるヘリウムが水素層の下に蓄積する。その後ヘリウム量がある臨界値に達すると、熱的に不安定なヘリウムのみのフラッシュが起こる |
| \(2 \times 10^{-10} > \dot{M}/(M_\odot \mathrm{yr}^{-1})\) | 熱的に不安定な水素燃焼が、フラッシュを引き起こす |
最近の観測: スーパーバースト
小質量X線連星の中には、X線バーストよりもさらに明るい突発現象を起こすことがあります。 これをスーパーバーストと呼びます。 これは Cornelisse et al. (2000)で初めて報告されました。 通常のX線バーストの総エネルギーは\(10^{39}\)ergですが、スーパーバーストでは\(10^{42}\)ergにも達します。 また通常のX線バーストが十秒程度で元の明るさに戻るのに対し、スーパーバーストでは1時間以上(場合によっては数日)かけてゆっくりと元の明るさに戻ります。 このスーパーバーストの原因は、降着した外層の下部に蓄積した炭素などの重元素の核融合燃焼による、特大の爆発と考えられています。 炭素などの重元素の核燃焼が点火することで、その上部に蓄積している水素やヘリウムの核燃焼にも点火が起き、特大の爆発が起こるのです。
参考文献
[1] Galloway et al., 2020, “The Multi-INstrument Burst ARchive (MINBAR)”
[2] Belian et al., 1972, “A Probable Precursor to the X-Ray Nova Centaurus XR-4”
[3] Bildsten, 1997, “Thermonuclear Burning on Rapidly Accreting Neutron Stars”
[4] Zand, 2017, “Understanding superbursts”
[5] Cornelisse et al., 2000, “The longest thermonuclear X-ray burst ever observed?. A BeppoSAX Wide Field Camera observation of 4U 1735-44”
[6] Aoyama et al., 2025, “Thermonuclear Superburst of MAXI J1752-457 Observed with NinjaSat and MAXI”
[7] Zand, “X-ray bursts and superbursts”
[8] 小山勝ニ, 嶺重慎, “ブラックホールと高エネルギー現象”