Table of contents

1. 磁気回転不安定性 (Magneto-Rotational Instability; MRI)
   1. 基礎方程式の線形化
   2. 問題設定
   3. ベクトル解析
   4. 計算
   5. 回転のないただのプラズマのとき
   6. 回転があるとき(簡単のため\(B_\varphi = 0\))
      1. 剛体回転のとき
      2. ケプラー回転のとき
      3. 銀河円盤(flat rotation)のとき
2. 物理的解釈
3. 直感的導出
4. 参考文献

磁気回転不安定性 (Magneto-Rotational Instability; MRI)

ブラックホールの周りを回っている降着円盤などは磁場を持ちます。その磁場によって円盤の中に乱流が起こるとされています。それを磁気回転不安定性(Magneto-Rotational Instability, MRI)と呼びます。降着円盤だけでなく、磁場を持っている円盤、例えば銀河円盤や原始惑星系円盤内部でも起こる重要な不安定性です。

基礎方程式の線形化

連続の式より

\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho {\bf v}) = 0 \tag{1}\]

運動方程式より

\[\left\{ \frac{\partial }{\partial t} + ({\bf v}\cdot \nabla) \right\} {\bf v} + \frac{1}{\rho} \nabla \left( P+ \frac{1}{8\pi} B^2 \right) - \frac{1}{4\pi \rho} ({\bf B} \cdot \nabla ) {\bf B} + \nabla \Phi = {\bf 0} \tag{2}\]

誘導方程式より

\[\frac{\partial {\bf B}}{\partial t} - \nabla \times ({\bf v} \times {\bf B}) = {\bf 0} \tag{3}\]

マクスウェル方程式より

\[\nabla \cdot {\bf B} = 0 \tag{4}\]

これらの式を線形化します。

\[{\bf v} = {\bf v}_0 + \delta {\bf v} , \ \rho = \rho_0 + \delta \rho, \ P = P_0 + \delta P, \ {\bf B} = {\bf B}_0 + \delta {\bf B}\]

\(0\)の添字が付いている量は非摂動量で、上の基礎方程式群を満たします。

\[(1) \ \Longrightarrow \  \frac{\partial \delta \rho}{\partial t} + \rho_0 \nabla \cdot \delta {\bf v} = 0 \tag{5}\] \[\begin{align} (2) \ \Longrightarrow \  & \frac{\partial \delta {\bf v}}{\partial t} + (\delta {\bf v} \cdot \nabla) {\bf v}_0 + ({\bf v}_0 \cdot \nabla ) \delta {\bf v} + \frac{1}{\rho_0} (\delta P + \frac{1}{4\pi} {\bf B}_0 \cdot \delta {\bf B}) \notag \\ & - \frac{\delta \rho}{\rho_0^2} \nabla (P_0 + \frac{1}{8\pi} B_0^2) - \frac{1}{4\pi \rho_0} (({\bf B}_0 \cdot \nabla) \delta {\bf B} + (\delta {\bf B} \cdot \nabla) {\bf B}_0) \notag \\ & + \frac{\delta \rho}{4\pi \rho_0^2} ({\bf B}_0 \cdot \nabla) {\bf B}_0 = {\bf 0} \tag{6} \end{align}\] \[(4) \ \Longrightarrow \  \nabla \cdot \delta {\bf B} = 0 \tag{7}\] \[\begin{align} (3) \ \Longrightarrow &\frac{\partial \delta {\bf B}}{\partial t} - \nabla \times (\delta {\bf v} \times {\bf B}_0 + {\bf v}_0 \times \delta {\bf B}) \notag \\ &= \frac{\partial \delta {\bf B}}{\partial t} - (({\bf B}_0 \cdot \nabla) \delta {\bf v}+ \delta {\bf v} (\nabla \cdot {\bf B}_0)- {\bf B}_0 (\nabla \cdot \delta {\bf v})- (\delta {\bf v}\cdot \nabla){\bf B}_0 \notag \\ &+ (\delta {\bf B} \cdot \nabla){\bf v}_0 + {\bf v}_0 (\nabla \cdot \delta {\bf B}) - \delta {\bf B} (\nabla \cdot {\bf v}_0)- ({\bf v}_0 \cdot \nabla )\delta{\bf B}) \notag \end{align}\]

(4), (7)式より

\[\frac{\partial \delta{\bf B}}{\partial t} - (({\bf B}_0 \cdot \nabla) \delta {\bf v} - {\bf B}_0 (\nabla \cdot \delta {\bf v}) - (\delta {\bf v}\cdot \nabla){\bf B}_0 + (\delta {\bf B} \cdot \nabla){\bf v}_0 - \delta {\bf B} (\nabla \cdot {\bf v}_0)- ({\bf v}_0 \cdot \nabla )\delta{\bf B}) = {\bf 0} \tag{8}\]

問題設定

ここまでは一般論です。これ以降は、磁気回転不安定性を議論するための具体的な背景を考えていくことにしましょう。
円柱座標\((R, \varphi, z)\)のもとで\(z\)軸周りを角速度\(\Omega(R)\)で回転している系を考えます。すなわち\({\bf v}_0 = v_{0\varphi} {\bf e}_\varphi = R\Omega(R) {\bf e}_\varphi\)。平衡状態では重力と遠心力が釣り合っているとします。一様な背景磁場は\({\bf B}_0 = (0, B_{0\varphi}, B_{0z})\)とします。摂動量は\(\delta \propto e^{-i\omega t + ikz}\)として、波数は\({\bf k} = (0, 0, k)\)のように書けるものとします。系は軸対称であり、式変形には局所解析近似(Local analysis)より\(k R \simeq R/\lambda \gg 1\)、すなわち\(0\)の添字のついている非摂動量の微分は無視します。

ベクトル解析

具体的な成分計算をする前に、円柱座標系における以下のベクトル演算を確認しておきましょう。

\[\nabla \cdot {\bf A} = \frac{1}{R} \frac{\partial}{\partial R} (R A_R) + \frac{1}{R} \frac{\partial A_\varphi}{\partial \varphi} + \frac{\partial A_z}{\partial z}\] \[({\bf A}\cdot \nabla){\bf C} = (({\bf A} \cdot {\rm grad}) C_r- \frac{A_\varphi C_\varphi}{R}) {\bf e}_R + (({\bf A} \cdot {\rm grad}) C_\varphi + \frac{A_\varphi C_R}{R}) {\bf e}_\varphi + (({\bf A}\cdot {\rm grad}) C_z) {\bf e}_z\]

ここで

\[{\bf A} \cdot {\rm grad} = A_R \frac{\partial }{\partial R} + \frac{A_\varphi}{R} \frac{\partial }{\partial \varphi} + A_z \frac{\partial }{\partial z}\]

です。

計算

\[\frac{\partial \delta \rho}{\partial t} + \rho_0 \frac{\partial \delta v_z}{\partial z} = -i\omega \delta \rho + ik \rho_0 \delta v_z = 0 \ \Longrightarrow \  -\omega \frac{\delta \rho}{\rho_0} + k \delta v_z = 0 \tag{9}\] \[(\delta {\bf v}\cdot \nabla) {\bf v}_0 = -\frac{\delta v_\varphi v_{0\varphi}}{R} {\bf e}_R + \delta v_R \frac{\partial v_{0\varphi}}{\partial R} {\bf e}_\varphi = -\Omega \delta v_\varphi {\bf e}_R + \delta v_R \frac{\partial }{\partial R} (R \Omega ) {\bf e}_\varphi\] \[({\bf v}_0 \cdot \nabla ) \delta {\bf v} = -\frac{v_{0\varphi} \delta v_\varphi}{R} {\bf e}_R + \frac{v_{0\varphi} \delta v_R}{R} {\bf e}_\varphi = -\Omega \delta v_\varphi {\bf e}_R + \Omega \delta v_R {\bf e}_\varphi\] \[\begin{align} ({\bf B}_0 \cdot \nabla) \delta {\bf B} &= (B_{0z} \frac{\partial \delta B_R}{\partial z} - \frac{B_{0\varphi} \delta B_\varphi}{R}) {\bf e}_R + (B_{0z} + \frac{\partial \delta B_\varphi}{\partial z} + \frac{B_{0\varphi \delta B_R}}{R}) {\bf e}_\varphi + B_{0z} \frac{\partial \delta B_z}{\partial z} {\bf e}_z \notag \\ &= (ikB_{0z} \delta B_R - \frac{B_{0\varphi} \delta B_\varphi}{R}) {\bf e}_R + (ikB_{0z} \delta B_\varphi + \frac{B_{0\varphi} \delta B_R}{R}) {\bf e}_\varphi + ik B_{0z} \delta B_z {\bf e}_z \notag \\ &\underbrace{\simeq}_{kR \gg 1} ik B_{0z} \delta B_R {\bf e}_R + ikB_{0z} \delta B_\varphi {\bf e}_\varphi + ik B_{0z} \delta B_z {\bf e}_z \notag \end{align}\] \[(\delta {\bf B} \cdot \nabla) {\bf B}_0 = - \frac{\delta B_\varphi B_{0\varphi}}{R} {\bf e}_R + (\delta B_R \frac{\partial B_{0\varphi}}{\partial R} + \delta B_z \frac{\partial B_{0\varphi}}{\partial z}) {\bf e}_\varphi + (\delta B_R \frac{\partial B_{0z}}{\partial R} + \delta B_z \frac{\partial B_{0z}}{\partial z}){\bf e}_z \underbrace{\simeq}_\mathrm{Local \ analysis} -\frac{\delta B_\varphi B_{0\varphi}}{R} {\bf e}_R\] \[({\bf B}_0 \cdot \nabla){\bf B}_0 = -\frac{B_{0\varphi}^2}{R} {\bf e}_R + B_{0z} \frac{\partial B_{0\varphi}}{\partial z} {\bf e}_\varphi + B_{0z} \frac{\partial B_{0z}}{\partial z} {\bf e}_z \underbrace{\simeq}_\mathrm{Local \ analysis} - \frac{B_{0\varphi}^2}{R} {\bf e}_R\] \[\begin{align} ({\bf B}_0 \cdot \nabla)\delta {\bf v} &= (B_{0z} \frac{\partial \delta v_R}{\partial z} - \frac{B_{0\varphi} \delta v_\varphi}{R}) {\bf e}_R + (B_{0z} \frac{\partial \delta v_\varphi}{\partial z} + \frac{B_{0\varphi} \delta v_R}{R}) {\bf e}_\varphi + B_{0z} \frac{\partial \delta v_z}{\partial z} {\bf e}_z \notag \\ &= (ikB_{0z} \delta v_R - \frac{B_{0\varphi} \delta v_\varphi}{R}) {\bf e}_R + (ikB_{0z} \delta v_\varphi + \frac{B_{0\varphi} \delta v_R}{R}) {\bf e}_\varphi + ikB_{0z} \delta v_z {\bf e}_z \notag \\ &\underbrace{\simeq}_{kR \gg 1} ikB_{0z} \delta v_R {\bf e}_R + ikB_{0z} \delta v_\varphi {\bf e}_\varphi + ikB_{0z} \delta v_z {\bf e}_z \notag \end{align}\] \[{\bf B}_0 (\nabla \cdot \delta {\bf v}) = {\bf B}_0 (\frac{1}{R} \frac{\partial }{\partial R} (R \delta v_R) + \frac{\partial \delta v_z}{\partial z}) = (\frac{\delta v_R}{R} + ik\delta v_z) {\bf B}_0 \underbrace{\simeq}_{kR \gg 1} ik \delta v_z {\bf B}_0\] \[(\delta {\bf v} \cdot \nabla){\bf B}_0 = -\frac{\delta v_\varphi B_{0\varphi}}{R} {\bf e}_R + (\delta v_R \frac{\partial B_{0\varphi}}{\partial R} + \delta v_z \frac{\partial B_{0\varphi}}{\partial z}) {\bf e}_{\varphi} + (\delta v_R \frac{\partial B_{0z}}{\partial R} + \delta v_z \frac{\partial B_{0z}}{\partial z}) {\bf e}_{z} \underbrace{\simeq}_\mathrm{Local \ analysis} - \frac{\delta v_\varphi B_{0\varphi}}{R} {\bf e}_R\] \[(\delta {\bf B} \cdot \nabla) {\bf v}_0 = -\frac{\delta B_\varphi v_{0\varphi}}{R} {\bf e}_R + \delta B_R \frac{\partial v_{0\varphi}}{\partial R} {\bf e}_\varphi = -\Omega \delta B_\varphi {\bf e}_R + \delta B_R \frac{\partial }{\partial R} (R\Omega) {\bf e}_\varphi\] \[\delta {\bf B} (\nabla \cdot {\bf v}_0) = 0\] \[({\bf v}_0 \cdot \nabla) \delta {\bf B} = -\frac{v_{0\varphi} \delta B_\varphi}{R} {\bf e}_R + \frac{v_{0\varphi} \delta B_R}{R} {\bf e}_\varphi = -\Omega \delta B_\varphi {\bf e}_R + \Omega \delta B_R {\bf e}_\varphi\]

(6)式の\(R\)成分より

\[\begin{align} &-i\omega \delta v_R - 2\Omega \delta v_\varphi - \frac{\delta \rho}{\rho_0^2} \frac{\partial P_0}{\partial R} - \frac{\delta \rho}{8\pi \rho_0^2} \frac{\partial }{\partial R} (B_{0\varphi}^2 + B_{0z}^2) - \frac{1}{4\pi \rho_0} (ik B_{0z} \delta B_R - \frac{\delta B_\varphi B_{0\varphi}}{R}) - \frac{\delta \rho}{4\pi \rho_0^2} \frac{B_{0\varphi}^2}{R} \notag \\ &\underbrace{\simeq}_\mathrm{Local \ analysis} - i \omega \delta v_R - 2\Omega \delta v_\varphi - \frac{\delta \rho}{\rho_0} \underbrace{((\frac{1}{\rho_0} \frac{\partial P_0}{\partial R} + \frac{1}{8\pi \rho_0} \frac{\partial }{\partial R} (B_{0\varphi}^2 + B_{0z}^2)) + \frac{1}{4\pi \rho_0} \frac{B_{0\varphi}^2}{R})}_{非摂動状態のR方向の運動方程式}-\frac{1}{4\pi \rho_0} ikB_{0z} \delta B_R \notag \\ &\underbrace{\simeq}_{\delta \rho/\rho_0 \ll 1} - i\omega \delta v_R - 2\Omega \delta v_\varphi - \frac{ik}{4\pi \rho_0} B_{0z} \delta B_R = 0 \tag{10} \end{align}\]

(6)式の\(\varphi\)成分より

\[\begin{align} -i\omega \delta v_\varphi + \delta v_R \frac{\partial}{\partial R} (R\Omega) + \Omega \delta v_R -\frac{1}{4\pi \rho_0} ik B_{0z} \delta B_\varphi &= -i\omega \delta v_\varphi + \delta v_R (R \frac{\partial \Omega}{\partial R} + 2\Omega) -\frac{ik}{4\pi \rho_0} B_{0z} \delta B_\varphi \notag \\ &= -i\omega \delta v_\varphi + \frac{\delta v_R}{R} (R^2 \frac{\partial \Omega}{\partial R} + 2R \Omega) - \frac{ik}{4\pi \rho_0} B_{0z} \delta B_\varphi \notag \\ &= - i\omega \delta v_\varphi + \delta v_R \frac{\kappa^2}{2\Omega} - \frac{ik}{4\pi \rho_0} B_{0z} \delta B_\varphi = 0 \tag{11} \end{align}\]

ここで

\[\kappa^2 \equiv \frac{2\Omega}{R} \frac{\partial }{\partial R} (R^2 \Omega)\]

はエピサイクリック振動数です。
(6)式の\(z\)成分より

\[\begin{align} &-i\omega \delta v_z + \frac{1}{\rho_0} (ik\delta P + \frac{1}{4\pi} ik B_{0\varphi} \delta B_\varphi + \frac{1}{4\pi} i k B_{0z} \delta B_z) - \frac{\delta \rho}{\rho_0^2} \frac{\partial P_0}{\partial z} - \frac{\delta \rho}{8\pi \rho_0^2} \frac{\partial }{\partial z} (B_{0\varphi}^2 + B_{0z}^2) - \frac{ik}{4\pi \rho_0} B_{0z} \delta B_z \notag \\ &= -i \omega \delta v_z + \frac{1}{\rho_0} (ik \delta P + \frac{1}{4\pi} i k B_{0\varphi} \delta B_\varphi) - \frac{\delta \rho}{\rho_0} \underbrace{(\frac{1}{\rho_0} \frac{\partial P_0}{\partial z} + \frac{1}{8\pi \rho_0} \frac{\partial}{\partial z} (B_{0 \varphi}^2 + B_{0z}^2))}_{非摂動状態のz方向の運動方程式} \notag \\ &\underbrace{\simeq}_{\delta \rho/\rho_0 \ll 1} -i\omega \delta v_z + \frac{ik}{\rho_0} \delta P + \frac{ik}{4\pi \rho_0} B_{0\varphi} \delta B_\varphi = 0 \tag{12} \end{align}\]

(8)式の\(R\)成分より

\[-i\omega \delta B_R - (ikB_{0z} \delta v_R + \frac{\delta v_\varphi B_{0\varphi}}{R} -\Omega \delta B_\varphi + \Omega \delta B_\varphi) \underbrace{=}_{kR \gg 1} -i\omega \delta B_R -ik B_{0z} \delta v_R = 0 \tag{13}\]

(8)式の\(\varphi\)成分より

\[-i\omega \delta B_\varphi - (ikB_{0z} \delta v_\varphi - ik\delta v_z B_{0\varphi} + \delta B_R \frac{\partial }{\partial R} (R\Omega) - \Omega \delta B_R) = -i\omega \delta B_\varphi - ik (B_{0z} \delta v_\varphi - \delta v_z B_{0\varphi}) - \delta B_R \frac{d \Omega}{d \ln R} \tag{14} = 0\]

(8)式の\(z\)成分より

\[-i\omega \delta B_z = 0 \tag{15}\]

さらに状態方程式は、系が断熱的な運動をしていると仮定して

\[\frac{P_0}{\rho_0^\gamma} = \frac{(P_0 + \delta P)}{(\rho_0 + \delta \rho)^\gamma} \simeq (P_0 + \delta P) \frac{1}{\rho_0^\gamma} (1-\gamma \frac{\delta \rho}{\rho_0}) = \frac{P_0}{\rho_0^\gamma} - \gamma \frac{P_0}{\rho_0^\gamma} \frac{\delta \rho}{\rho_0} + \frac{\delta P}{\rho_0^\gamma} \ \Longrightarrow \ \delta P = \frac{\gamma P_0}{\rho_0} \delta \rho = C_s^2 \delta \rho \tag{16}\]

とします。では具体的な分散関係式を導出しましょう。

回転のないただのプラズマのとき

(10), (13)式より

\[-i\omega \delta v_R - \frac{ik}{4\pi \rho_0} B_{0z} (-\frac{kB_{0z} \delta v_R}{\omega}) = 0 \ \Longrightarrow \ (\omega^2 - k^2 v_{Az}^2) \delta v_R = 0\]

となります。よって\(R\)方向には横波のアルヴェーン波が伝播することがわかります。続いて\(\varphi, z\)方向(磁場に沿った方向)の分散関係式を求めましょう。

\[(11) \ \Longrightarrow \ \delta v_\varphi = - \frac{1}{\omega} \frac{kB_{0z}}{4\pi \rho_0} \delta B_\varphi\] \[\begin{align} (9), (12), (16) &\Longrightarrow \  -\omega \delta v_z + \frac{k}{\rho_0} \frac{\gamma P_0}{\rho_0} \delta \rho + \frac{B_{0\varphi} k}{4\pi \rho_0} \delta B_\varphi = -\omega \delta v_z + \frac{k}{\rho_0} \gamma P_0 \frac{k}{\omega} \delta v_z + \frac{B_{0\varphi} k}{4\pi \rho_0} \delta B_\varphi = 0 \notag \\ &\Longrightarrow \  (-\omega + \frac{k^2 C_s^2}{\omega}) \delta v_z + \frac{B_{0\varphi} k}{4\pi \rho_0} \delta B_\varphi = 0 \notag \end{align}\] \[\begin{align} (14) &\Longrightarrow \  -i\omega \delta B_\varphi = ik B_{0z} (-\frac{1}{\omega} \frac{k B_{0z}}{4\pi \rho_0}) \delta B_\varphi -ikB_{0\varphi} \delta v_z = -\frac{k^2 B_{0z}^2}{4\pi \rho_0 \omega} \delta B_\varphi - ik B_{0\varphi} \delta v_z \notag \\ &\Longrightarrow \  (\omega - \frac{k^2 v_{Az}^2}{\omega}) \delta B_\varphi = k B_{0\varphi} \delta v_z \ \Longrightarrow \ \delta B_\varphi = \frac{kB_{0\varphi} \omega}{\omega^2 - k^2 v_{Az}^2} \delta v_z \notag \end{align}\]

以上の式より

\[\begin{align} &(-\omega^2 + k^2 C_s^2) \delta v_z + \frac{B_{0\varphi}^2 k^2\omega^2}{4\pi \rho_0(\omega^2 - k^2 v_{Az}^2)} \delta v_z = (-\omega^2 + k^2 C_s^2 + \frac{v_{A\varphi}^2 k^2\omega^2}{\omega^2 -k^2 v_{Az}^2}) \delta v_z = 0 \notag \\ &\Longrightarrow \ \omega^4 - k^2\omega^2 (C_s^2 + \underbrace{v_{Az}^2 + v_{A\varphi}^2}_{v_{A}^2}) + k^4 v_{Az}^2 C_s^2 = 0 \notag \end{align}\]

よって\(\varphi, z\)方向から速い磁気音波と遅い磁気音波の分散関係式が得られます。

回転があるとき(簡単のため\(B_\varphi = 0\))

\(r, \varphi\)方向の分散関係式を求めてみましょう。

\[(13) \ \Longrightarrow \  \delta B_R = -\frac{k B_{0z}}{\omega} \delta v_R\] \[(14) \ \Longrightarrow \  -i\omega \delta B_\varphi = -\frac{kB_{0z}}{\omega} \delta v_R \frac{d\Omega}{d \ln R} + ikB_{0z} \delta v_\varphi \ \Longrightarrow \  \delta B_\varphi = \frac{kB_{0z}}{i\omega^2} \delta v_R \frac{d \Omega}{d \ln R} - \frac{kB_{0z}}{\omega} \delta v_\varphi\] \[\begin{align} (11) &\Longrightarrow \  -i\omega \delta v_\varphi + (2\Omega + \frac{d\Omega}{d \ln R}) \delta v_R - i\frac{kB_{0z}}{4\pi \rho_0} (\frac{kB_{0z}}{i\omega^2} \delta v_R \frac{d\Omega}{d\ln R} -\frac{k B_{0z}}{\omega} \delta v_\varphi) = 0 \notag \\ &\Longrightarrow \ (2\Omega + \frac{\omega^2 - k^2 v_{Az}^2}{\omega^2} \frac{d\Omega}{d\ln R}) \delta v_R + i \frac{\omega^2 - k^2 v_{Az}^2}{\omega} \delta v_\varphi = 0 \notag \end{align}\] \[(10) \ \Longrightarrow \  -i\omega \delta v_R - 2\Omega \delta v_\varphi + \frac{ik}{4\pi \rho_0} \frac{k B_{0z}}{\omega} \delta v_R = i\frac{k^2 v_{Az}^2 - \omega^2}{\omega} \delta v_R -2\Omega \delta v_\varphi = 0\]

以上より

\[\left( \begin{array}{cc} i\frac{k^2 v_{Az}^2 - \omega^2}{\omega} & -2\Omega \\ 2\Omega + \frac{\omega^2 -k^2 v_{Az}^2}{\omega^2} \frac{d\Omega}{d\ln R} & i\frac{k^2 v_{Az}^2 - \omega^2}{\omega} \end{array} \right) \left( \begin{array}{c} \delta v_R\\ \delta v_\varphi \end{array} \right) = {\bf 0} \tag{17}\]

任意の\(\delta {\bf v} = (\delta v_R, \delta v_\varphi)\)でこの式が成り立つためには、係数行列の行列式が0であれば良いことがわかります。

\[\begin{align} &{\rm det} \left| \begin{array}{cc} i\frac{k^2 v_{Az}^2 - \omega^2}{\omega} & -2\Omega \\ 2\Omega + \frac{\omega^2 -k^2 v_{Az}^2}{\omega^2} \frac{d\Omega}{d\ln R} & i\frac{k^2 v_{Az}^2 - \omega^2}{\omega} \end{array} \right| = -\frac{(k^2 v_{Az}^2-\omega^2)^2}{\omega^2} + 4\Omega^2 + \frac{\omega^2 - k^2 v_{Az}^2}{\omega^2} \frac{d\Omega^2}{d\ln R} = 0 \notag \\ &\Longrightarrow \  \omega^2 - k^2 v_{Az}^2 = \pm \sqrt{4\Omega^2 \omega^2 + (\omega^2 - k^2 v_{Az}^2) \frac{d\Omega^2}{d\ln R}} \tag{18} \end{align}\]

剛体回転のとき

\(d\Omega/dR = 0\)より

\[(\#\#1) \ \Longrightarrow \  \omega^2 -k^2 v_{Az}^2 = \pm \sqrt{4\Omega^2 \omega^2} \ \Longrightarrow \  \left( \frac{\omega}{\Omega} \right)^2 = \left(\frac{kv_{Az}}{\Omega}\right)^2 \pm \sqrt{4 \left( \frac{\omega}{\Omega} \right)^2 }\]

分散関係式は求まりましたが、ここでさらに(##0)式から

\[\frac{i\delta v_\varphi}{\delta v_R} = - \frac{2\Omega}{k^2 v_{Az}^2 -\omega^2} \omega = \pm 1\]

より\(\delta v_\varphi = \mp i \delta v_R\)としてみましょう。すると

\[\delta {\bf v} = \delta v_R {\bf e}_R + \delta v_\varphi {\bf e}_\varphi = \delta v_R ({\bf e}_R \mp i {\bf e}_\varphi)\]

となります。速い位相速度を持つ波は、円盤と同じ回転方向に回る円偏波、遅い位相速度を持つ波は円盤の回転方向とは逆方向に回る円偏波と考えることができます。
剛体回転の場合、どちらも\(\omega^2\)は負になることがなく、不安定でないことがわかります。

ケプラー回転のとき

\[\Omega^2 = \frac{GM}{R^3} \ \Longrightarrow \  \frac{d\Omega^2}{dR} = -3 \frac{GM}{R^4} = -3\Omega^2\frac{1}{R} \ \Longrightarrow \  \frac{d\Omega^2}{d\ln R} = -3\Omega^2\]

より

\[(\#\#1) \ \Longrightarrow \  \omega^2 - k^2 v_{Az}^2 = \pm \sqrt{\Omega^2 \omega^2 + 3\Omega^2 k^2 v_{Az}^2}\]

\(0<k<\sqrt{3}\Omega / v_{Az}\)では\(\omega^2 < 0\)となり、これは不安定となります。最大成長率はおよそ\(\nu_{\rm MRI} \simeq 0.75 \Omega\)となります。

銀河円盤(flat rotation)のとき

\[\Omega^2 = \frac{v_0^2}{R^2} \ \Longrightarrow \  \frac{d\Omega^2}{dR} = -2 \frac{\Omega^2}{R} \ \Longrightarrow \  \frac{d\Omega^2}{d\ln R} = -2\Omega^2\]

より

\[(\#\#1) \ \Longrightarrow \  \omega^2 - k^2 v_{Az}^2 = \pm \sqrt{2 \Omega^2 \omega^2 + 2\Omega^2 k^2 v_{Az}^2}\]

\(0<k<\sqrt{2} \Omega/ v_{Az}\)では\(\omega^2 < 0\)となり、これは不安定です。最大成長率はおよそ\(\nu_{\rm MRI} \simeq 0.5 \Omega\)です。

物理的解釈

先ほどの円偏波の話に少し戻り、MRIの物理過程について解説します。今は基底ベクトルに\({\bf e}_R, {\bf e}_\varphi\)を用いているので、これは円盤とともに回転している系からみたときの話になります。円盤の外にいる、回転していない系からこれを観察してみると、速い位相速度の円偏波は回転円盤よりも大きな角速度で回転するモードになります。遅い位相速度の円偏波は回転円盤よりも小さな角速度で回転するモードに対応しています。安定点から摂動を加えられた時に、大きな角速度で回転しているモードでは、遠心力が大きいので、流体要素は遠心力を復元力とした早い周期のエピサイクリック運動を行うことができます。磁気張力による角運動量輸送のタイムスケールよりもエピサイクリック振動周期が短いので、磁力線は棚引かず、不安定になりません。一方で、小さな角速度で回転しているモードは遠心力が弱いので流体要素のエピサイクリック振動周期が長くなります。エピサイクリック運動で元の位置に戻るよりも先に、磁気張力による角運動量輸送が行われてしまい、不安定となります。

直感的導出

ここまで厳密な数値解析から、安定なモードと不安定なモードの2種類が存在することがわかりましたが、ここでは定性的にこの不安定性を導出することを模索しましょう。

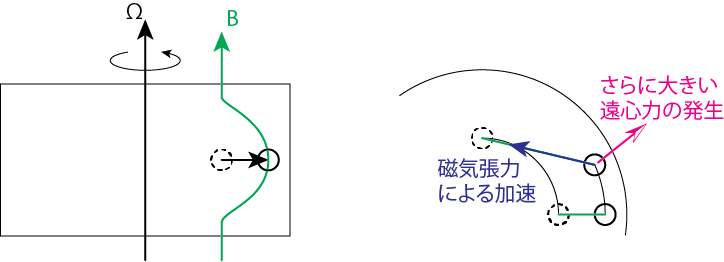
ある重力場中で安定に差動回転をしているプラズマ円盤があるとします。そこに回転軸方向に磁場が加わっていたとしましょう。磁力線が突き刺さった半径\(R\)の円運動している流体要素に摂動を加えます。ここで加えた摂動は動径方向に小さく加えたものであり、角運動量は保存しているものとします。角運動量を保存したまま外側の\(R + \Delta R\)に移動したため、その分だけ角速度は遅くなります。よって磁力線はより大きく変形し磁気張力が加わります。すると磁気張力により回転方向の角速度が働くため、流体要素の角速度を大きくします。しかし、それでは\(R + \Delta R\)の位置での重力よりも遠心力が大きくなるので、より外側に追いやられてしまいます。その分磁力線がさらに伸ばされ、より大きな磁気張力が働きます。このように、磁力線が存在することによって角運動量の輸送が起こる一連の過程がMRIの本質です。
この考え方から、MRIの起こる条件を見積もってみましょう。以下ではケプラー回転を仮定します。動径方向の釣り合いの式より

\[(重力) = \frac{GM}{R^2} \ \rightarrow \ \frac{GM}{(R+\Delta R)^2} = \frac{GM}{R^2} \frac{1}{(1 + \frac{\Delta R}{R})^2} \simeq \frac{GM}{R^2} \left(1-2\frac{\Delta R}{R} \right)\] \[(遠心力) = R \Omega(R)^2 \ \rightarrow \  (R + \Delta R) \Omega(R)^2\]

遠心力部分に「回転方向に働く磁気張力による角速度を一定にしようとする効果」が入っています。ケプラー回転より\(\Omega (R) = \sqrt{GM/R^3}\)です。

\[\therefore \ -(重力) + (遠心力) = 2\frac{GM}{R^3} \Delta R + \Delta \Omega(R)^2 = 3\Delta R \Omega(R)^2\]

動径方向に働く磁気張力を考えましょう。以下の図のように変形した磁力線の曲率半径を\(\xi\)とすると

\[(磁気張力) = \frac{1}{4\pi \rho} \frac{B^2}{\xi} = \frac{v_{A}^2}{\xi}\]

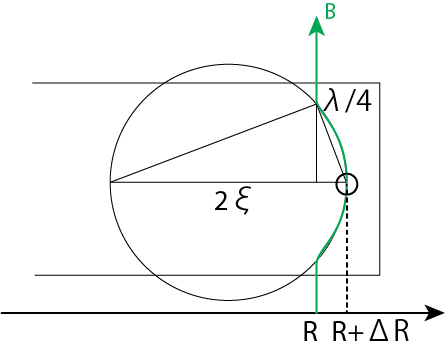
図のように三角形の相似を用いると

\[2\xi : \frac{\lambda}{4} = \frac{\lambda}{4} : \Delta R \ \Longrightarrow \  \xi = \frac{\lambda^2}{32\Delta R} = \frac{\pi^2}{8\Delta R} \frac{1}{k^2}\]

よって磁気張力の大きさは

\[\frac{8}{\pi^2} \Delta R k^2 v_A^2 \simeq \Delta R k^2 v_A^2\]

(重力と遠心力の合力) > 動径方向に働く磁気張力のとき、不安定となるので

\[3\Omega^2 \Delta R > \Delta R k^2 v_A^2 \ \Longrightarrow \  0 < k < \frac{\sqrt{3}\Omega}{v_A}\]

で不安定となります。これは厳密に式変形をした場合の不安定条件と一致します。

参考文献

• Balbus & Hawley, 1991
• 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”