ブラソフ方程式 (Vlasov equation)

ここでは2体緩和が無視できるような、無衝突重力多体系を記述するのに必要となるブラソフ方程式(Vlasov equation)を導出します。これはボルツマン方程式(Boltzmann equation)の衝突項を無視したものとして知られており、またの名を無衝突ボルツマン方程式(collisionless Boltzmann equation)とも呼ばれています。非常に多数の粒子系を扱う場合には、それらを一点ずつ表現するのではなく、ある分布関数に従うものとして表現する方が便利です。ブラソフ方程式は、無衝突系での分布関数の時間発展を記述しています。

リウビルの定理 (Liouville’s theorem)

まずは方程式を導出するために必要となる定理を導出しましょう。
\(N\)個の粒子が存在する力学系を考え、それらは一つ一つが位置\(\mathbf{q}_i = (q_{i1}, q_{i2}, q_{i3})\)と運動量\(\mathbf{p}_i = (p_{i1}, p_{i2}, p_{i3})\)のような自由度を持つとします。以下では座標と運動量をまとめて\(\mathbf{q} = (\mathbf{q}_1, \mathbf{q}_2, \dots, \mathbf{q}_N), \mathbf{p} = (\mathbf{p}_1, \mathbf{p}_2, \dots, \mathbf{p}_N)\) 運動エネルギーは位置と運動量に依存するため\(T(\mathbf{q}, \mathbf{p})\)のような関数系で書かれ、さらに系のポテンシャルエネルギーを\(W(\mathbf{q})\)のように書くと、この系のハミルトニアンは

\[H(\mathbf{q}, \mathbf{p}) = T(\mathbf{q}, \mathbf{p}) + W(\mathbf{q}) \tag{1}\]

のようになります。すると、ハミルトンの運動方程式は

\[\frac{dq_{ij}}{dt} = \frac{\partial H}{\partial p_{ij}} (\mathbf{q}, \mathbf{p}), \quad \frac{dp_{ij}}{dt} = - \frac{\partial H}{\partial q_{ij}} (\mathbf{q}, \mathbf{p}) \quad (i = \{1, 2, \dots, N\}, j = \{1, 2, 3\} ) \tag{2}\]

のようになります。この\(N\)粒子系について、位相空間上で考えてみましょう。\(N\)個の粒子が位置と運動量について6つの自由度を持つため、この系の自由度は\(6N\)です。よって位相空間は\(6N\)次元となります。しかしここでは簡単のため、\(i\)番目の粒子の\(j\)方向に対する位置と運動量、すなわち\((q_{ij}, p_{ij})\)平面を切り出して考えてみましょう。

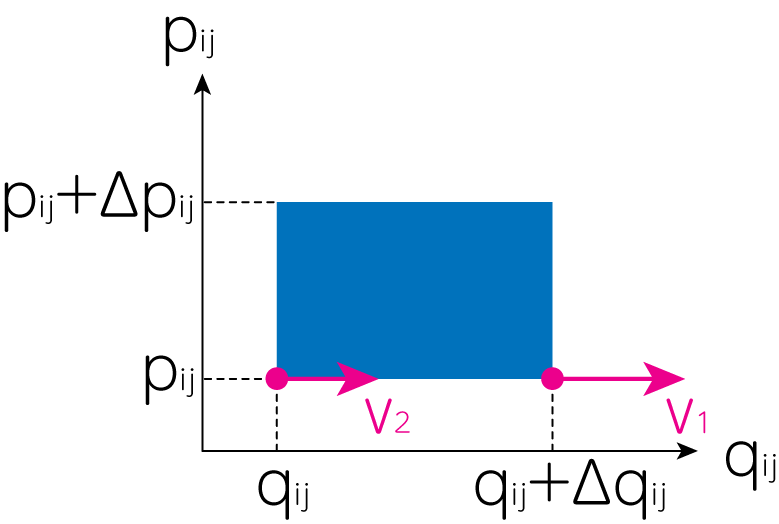
この位相空間上の平面内において、粒子群が上図のように面積\(S = \Delta q_{ij} \Delta p_{ij}\)を形成しているとします。ここで\(\Delta q_{ij}, \Delta p_{ij} \ll 1\)とします。今、この面積が、\(v_2 = \dot{q}_{ij} (q_{ij}), v_1 = \dot{q}_{ij} (q_{ij} + \Delta q_{ij})\)のように位相空間上で運動をしたと考えましょう。するとその速度の差分は

\[\Delta v \equiv v_1 - v_2 = \dot{q}_{ij} (q_{ij} + \Delta q_{ij}) - \dot{q}_{ij} (q_{ij}) \underbrace{\simeq}_{\Delta q_{ij} \ll 1} \dot{q}_{ij} (q_{ij}) + \frac{\partial \dot{q}_{ij}}{\partial q_{ij}} \Delta q_{ij} - \dot{q}_{ij} (q_{ij}) = \frac{\partial \dot{q}_{ij}}{\partial q_{ij}} \Delta q_{ij} \tag{3}\]

のように計算されます。ここから上図の面積\(S\)の、\(q_{ij}\)方向の長さの変化は

\[\delta (\Delta q_{ij}) = \Delta v \delta t = \frac{\partial \dot{q}_{ij}}{\partial q_{ij}} \Delta q_{ij} \delta t \tag{4}\]

同じように\(p_{ij}\)方向についても考えれば、\(p_{ij}\)方向の長さの変化は

\[\delta (\Delta p_{ij}) = \frac{\partial \dot{p}_{ij}}{\partial p_{ij}} \Delta p_{ij} \delta t \tag{5}\]

となります。この2つから、面積\(S\)の変化分は

\[\begin{align} \Delta S &= \left\{ \Delta q_{ij} + \delta (\Delta q_{ij})\right\}\left\{ \Delta p_{ij} + \delta (\Delta p_{ij})\right\} - \Delta q_{ij} \Delta p_{ij} = \Delta q_{ij} \delta (\Delta p_{ij}) + \Delta p_{ij} \delta (\Delta q_{ij}) + \delta (\Delta q_{ij}) \delta (\Delta p_{ij}) \notag \\ &\simeq \Delta q_{ij} \frac{\partial \dot{p}_{ij}}{\partial p_{ij}} \Delta p_{ij} \delta t + \Delta p_{ij} \frac{\partial \dot{q}_{ij}}{\partial q_{ij}} \Delta q_{ij} \delta t = \Delta q_{ij} \Delta p_{ij} \delta t \left( \frac{\partial \dot{q}_{ij}}{\partial q_{ij}} + \frac{\partial \dot{p}_{ij}}{\partial p_{ij}}\right) \tag{6} \end{align}\]

のように計算されます。ここで\(\delta t \ll 1\)とし、\(\delta t\)の一次までを考えました。この式に(2)式を適用すると

\[\Delta S = \Delta q_{ij} \Delta p_{ij} \delta t \left\{ \frac{\partial}{\partial q_{ij}} \left( \frac{\partial H}{\partial p_{ij}}\right)+ \frac{\partial}{\partial p_{ij}} \left( - \frac{\partial H}{\partial q_{ij}}\right) \right\} = 0 \tag{6}\]

のようになります。これは位相空間内で粒子の分布が作る面積(\(6N\)次元なので、厳密には体積)は不変であることを意味します。これをリウビルの定理と呼びます。

ブラソフ方程式の導出

リウビルの定理は、位相空間内の流れ(運動の軌跡)に沿って分布関数\(f(\mathbf{q}, \mathbf{p}, t)\)の占める体積は不変である、ということを言っています。このことから、微小時間\(\Delta t\)経過後の分布関数\(f(\mathbf{q} + \dot{q}\Delta, \mathbf{p} + \dot{p} \Delta t, t + \Delta t)\)との間に

\[f(\mathbf{q}, \mathbf{p}, t) = f(\mathbf{q} + \dot{\mathbf{q}}\Delta t, \mathbf{p} + \dot{\mathbf{p}} \Delta t, t + \Delta t) \tag{7}\]

が成り立ちます。右辺を\(\Delta t\)の一次まででテイラー展開すると

\[f(\mathbf{q}, \mathbf{p}, t) = f(\mathbf{q}, \mathbf{p}, t) + \frac{\partial f}{\partial t} \Delta t + \frac{\partial f}{\partial \mathbf{q}} \cdot \dot{\mathbf{q}} \Delta t + \frac{\partial f}{\partial \mathbf{p}} \cdot \dot{\mathbf{p}} \Delta t \ \Longrightarrow \ \frac{\partial f}{\partial t} + \frac{\partial f}{\partial \mathbf{q}} \cdot \dot{\mathbf{q}} + \frac{\partial f}{\partial \mathbf{p}} \cdot \dot{\mathbf{p}} = 0 \tag{8}\]

ここまでは\(\mathbf{q}, \mathbf{p}\)については、その形については特に触れてきませんでした。ここではさらに扱いやすいように、\(\mathbf{q} \rightarrow \mathbf{x}\)(普通の3次元座標)、\(\mathbf{p} \rightarrow \dot{\mathbf{x}} = \mathbf{v}\)(単位質量あたりの運動量)のようにしましょう。すると、重力多体系においては

\[\dot{\mathbf{p}} = \ddot{\mathbf{x}} = - \frac{\partial \Phi}{\partial \mathbf{x}} \tag{9}\]

のようになります。ここで\(\Phi\)は重力ポテンシャルです。以上より、\(f(\mathbf{q}, \mathbf{p}, t)\)を\(f(\mathbf{x}, \mathbf{v}, t)\)のように関数形を書き直せば

\[\frac{\partial f}{\partial t} + \mathbf{v} \cdot \nabla f - \nabla \Phi \cdot \frac{\partial f}{\partial \mathbf{v}} = 0 \tag{10}\]

のようになります。(10)式をブラソフ方程式と呼びます。

衝突がある場合には右辺に衝突に由来する項が入ります。

直感的な導出

ここまでリウビルの定理などを用いて数学的に導出してきましたが、以下のように直感的に考えることもできます。アナロジーとして非圧縮性流体を考えましょう。流体の密度を\(\rho\)とすると、この状況では\(\frac{D\rho}{Dt} = 0\)、すなわち流れに沿って流体要素の密度が不変と言えます。同様のことを6次元位相空間で考えます。無衝突の場合、6次元位相空間上の移動に沿って突然粒子数が増減することはなく、常に一定であるはずです。このことから

\[\frac{Df}{Dt} = \frac{\partial f}{\partial t} + \sum_{i=1}^6 v_i \frac{\partial f}{\partial x_i} = 0 \tag{11}\]

流体力学のラグランジュ微分と違うのは、第二項の微分の部分です。流体力学では\(x, y, z\)の空間3成分のみを考えれば大丈夫でしたが、今は\(x, y, z, v_x, v_y, v_z\)の位相空間の6成分で考えなければなりません。よって(11)式においては、\(x_1 = x, x_2 = y, x_3 = z\)は3次元空間の座標に対応し、\(x_4 = v_x, x_5 = v_y, x_6 = v_z\)はそれぞれその方向に対する速度となります。同様に\(v_1 = v_x, v_2 = v_y, v_3 = v_z, v_4 = a_x, v_5 = a_y, v_6 = a_z\)となります。ここで\(a_x, a_y, a_z\)はそれぞれ\(x, y, z\)方向の加速度です。重力多体系の場合、加速度は重力による力、すなわち\(- \frac{\partial \Phi}{\partial \mathbf{x}}\)のように書くことができます。よって第二項を分離して

\[\frac{\partial f}{\partial t} + \mathbf{v} \cdot \nabla f - \nabla \Phi \cdot \frac{\partial f}{\partial \mathbf{v}} = 0 \tag{12}\]

のように書けば、(10)式と同じものを得ることができます。

余談: 無衝突プラズマ系のブラソフ方程式

(10)式は重力多体系について成り立つ方程式でしたが、その前の(8)式は無衝突であればどのような系でも成り立ちます。有名なものとしては無衝突プラズマがあります。無衝突プラズマにおいては(9)式の力が

\[\dot{\mathbf{p}} = \ddot{\mathbf{x}} = \frac{q}{m} \left( \mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B} \right) \tag{13}\]

となります。最終的に

\[\frac{\partial f}{\partial t} + \mathbf{v} \cdot \frac{\partial f}{\partial \mathbf{x}} + \frac{q}{m} \left( \mathbf{E} + \frac{\mathbf{v}}{c} \times \mathbf{B} \right) \cdot \frac{\partial f}{\partial \mathbf{v}} = 0 \tag{14}\]

を得ます。実際にこれを数値計算で解くときには、分布関数\(f\)の時間発展と同時に、電場・磁場の時間発展をマクスウェル方程式

\[\frac{\partial \mathbf{E}}{\partial t} = c \nabla \times \mathbf{B} - 4\pi \mathbf{j} \tag{15}\] \[\frac{\partial \mathbf{B}}{\partial t} = - c \nabla \times \mathbf{E} \tag{16}\] \[\nabla \cdot \mathbf{E} = 4\pi \rho \tag{17}\] \[\nabla \cdot \mathbf{B} = 0 \tag{18}\]

も解いていきます。

参考文献

牧野淳一郎, “理論物理学特論I”