音響重力波 (acoustic gravity waves, gravito-acoustic wave)

ここでは圧力を復元力として伝播する音波と重力波がお互いに影響を及ぼし合った場合の波を考えます。

簡単な導出

音波の導出部分で出てきた分散関係式(20)において磁場と回転を無視(\(B =0, \boldsymbol{\Omega}=\mathbf{0}\))すると

\[\omega^2 \mathbf{v}_1 = C_s^2 \mathbf{k} (\mathbf{k} \cdot \mathbf{v}_1) + i (\gamma-1) g (\mathbf{k} \cdot \mathbf{v}_1) \mathbf{e}_z + i g v_{1z} \mathbf{k} \tag{1}\]

\(\mathbf{k} = (k_x, k_z), \mathbf{v}_1 = (v_{1x}, v_{1z})\)とすると

\[\begin{aligned} \omega^2 \mathbf{v}_1 &= \left( \begin{array}{c} C_s^2 (k_x v_{1x} + k_z v_{1z}) k_x + ig v_{1z} k_x \\ C_s^2 (k_x v_{1x} + k_z v_{1z}) k_z + i(\gamma-1) g (k_x v_{1x} + k_z v_{1z}) + ig v_{1z} k_z \end{array} \right) \\ &= \left( \begin{array}{c} C_s^2 k_x^2 v_{1x} + (C_s^2 k_z + ig) k_x v_{1z} \\ \{C_s^2 k_z + i(\gamma-1) g\} k_x v_{1x} + (i\gamma g + C_s^2 k_z) k_z v_{1z} \end{array} \right) = \left( \begin{array}{cc} C_s^2 k_x^2 & (C_s^2 k_z + ig) \\ \{C_s^2 k_z + i(\gamma-1) g \} k_x & (i\gamma g + C_s^2 k_z) k_z \end{array} \right) \mathbf{v}_1 \end{aligned}\]

よって

\[\left( \begin{array}{cc} C_s^2 k_x^2 - \omega^2 & (C_s^2 k_z + ig) k_x \\ \{C_s^2 k_z + i(\gamma-1) g \} k_x & (i\gamma g + C_s^2 k_z) k_z - \omega^2 \end{array} \right) \mathbf{v}_1 = \mathbf{0} \tag{2}\]

任意の\(\mathbf{v}_1\)でこれが成り立つためには、この式の係数行列の逆行列が存在してはなりません。よってこの行列式が0となる必要があります。

\[\begin{aligned} &(C_s^2 k_x^2 - \omega^2) \{ (i\gamma g + C_s^2 k_z) k_z - \omega^2\} - (C_s^2 k_z + ig)k_x \{ C_s^2 k_z + i (\gamma-1) g\} \\ &= \omega^4 - (C_s^2 k_x^2 + i \gamma g k_z + C_s^2 k_z^2) + C_s^2 k_x^2 (i\gamma g k_z + C_s^2 k_z^2) - (C_s^2 k_z + ig) \{ C_s^2 k_z + i (\gamma-1) g\} k_x \\ &= \omega^4 - \left( k_x^2 + k_z^2 + i\frac{\gamma g}{C_s^2} k_z\right) C_s^2 \omega^2 + C_s^2 k_x^2 (i\gamma g k_z + C_s^2 k_z^2) - \{ C_s^4 k_z^2 + i(\gamma-1) g C_s^2 k_z - (\gamma-1) g^2 \} k_x^2 \\ &= \omega^4 - \left\{ k_x^2 + \left( k_z + i \frac{\gamma g}{2 C_s^2} \right)^2 + \frac{\gamma^2 g^2}{4 C_s^4}\right\} C_s^2 \omega^2 + (\gamma-1) g^2 k_x^2 \\ &= 0 \end{aligned}\]

ここで

\[N^2 \equiv \frac{(\gamma-1) g^2}{C_s^2} , \quad N_s \equiv \frac{\gamma g}{2 C_s}, \quad \mathbf{k}' \equiv \mathbf{k} + i \frac{N_s^2}{C_s} \mathbf{e}_z, \quad \sin^2 \theta'_g \equiv 1 - \frac{k_z'^2}{k'^2} = \frac{k_x^2}{k'^2}\]

などを定義すると

\[\omega^4 - \left( k'^2 + \frac{N_s^2}{C_s^2} \right) C_s^2 \omega^2 + N^2 C_s^2 k'^2 \sin^2 \theta'_g = 0 \tag{3}\]

例えば\(\gamma = 5/3\)の理想気体の場合、\(N_s \simeq 1.02 N\)となります。よって\(N_s, N\)は同程度のオーダーです。またこれらは重力と浮力を復元力とする振動数、すなわちBrunt-Väisälä周波数を意味しており、一般に音波よりも大きく低い振動数です\((N, N_s \ll k' C_s)\)。

内部重力波モード(g-mode)と音波モード(p-mode)

\(\omega \ll k' C_s\)の波動を考えると、(3)式から\(\omega \simeq N \sin \theta'_g\)となります。これは内部重力波のモード(g-mode)です。逆に\(\omega \gg N\)のとき、\(\omega \simeq k' C_s\)となります。これは音波のモード(p-mode)です。この波が垂直方向に伝播するとき(\(\theta'_g =0\)のとき)、\(\omega^2 = N_s^2 + k'^2 C_s^2\)となり、\(\omega > N_s\)の波のみ存在しうると判断できます。
今度は垂直でない方向に伝播が許される波動の解(\(k'^2 > 0, \omega^2 >0\))を考えましょう。(3)式を解くと

\[\omega^2 = \frac{1}{2} \left( k'^2 C_s^2 + N_s^2 \pm \sqrt{(k'^2 C_s^2 + N_s^2)^2 - 4 N^2 C_s^2 k'^2 \sin^2 \theta'_g}\right) \tag{4}\]

より、波として許されるのは\(\omega < N \sin \theta'_g, \omega > N_s\)の2つがあることがわかります。振動数の大きいモードは基本的に音波によるモードですが、群速度は\(v_g < C_s\)、位相速度は\(v_p > C_s\)です。\(\omega \rightarrow N_s\)の極限では、\(v_p \rightarrow \infty, v_g \rightarrow 0\)となります。振動数の小さいモードは基本的に内部重力波によるモードで、位相速度は\(v_p < C_s\)です。\(\omega \rightarrow N \sin \theta'_g\)の極限では\(v_p \rightarrow 0\)となります。\(N_s\)と\(N \sin \theta'_g\)の間の振動数の波動は伝播できません(もしくは少しの距離伝播するけれども、そのうち減衰して消えていく)。しかし\(k'\)が純虚数の場合には振動振幅が指数的に増加することがあり得ます。実際には\(N \sin \theta'_g < \omega < N_s\)の波は定在波として存在することができますが、この場合には\(P_1\)と\(v_1\)の位相が反転しているためにエネルギーを伝播することはできません。
続いて、ある\(k_x, \omega\)に対して波動が垂直方向に伝播していくことができるかどうかを確認してみましょう。(3)式より

\[\begin{aligned} &\omega^2 - \left( k_x^2 + k'^2_z + \frac{N_s^2}{C_s^2} \right) C_s^2 \omega^2 + N^2 C_s^2 k_x^2 = \omega^2 (\omega^2 - N_s^2) - (\omega^2 - N^2) C_s^2 k_x^2 - k'^2_z C_s^2 \omega^2 = 0 \\ &\Longrightarrow \ \omega^2 (\omega^2 - N_s^2) - (\omega^2 - N^2) C_s^2 k_x^2 = k'^2_z C_s^2 \omega^2 \end{aligned}\]

\(k_x^2 > 0, \omega^2 > 0\)で垂直方向への伝播が許される、すなわち\(k'_z>0\)が成り立つには

\[\omega^2 (\omega^2 - N_s^2) > (\omega^2 - N^2) C_s^2 k_x^2 \tag{5}\]

でなければなりません。これが成り立っている領域を\(\omega - k_x\)平面で図示すると下図のようになります。この図のことをdiagnostic diagramと呼びます。

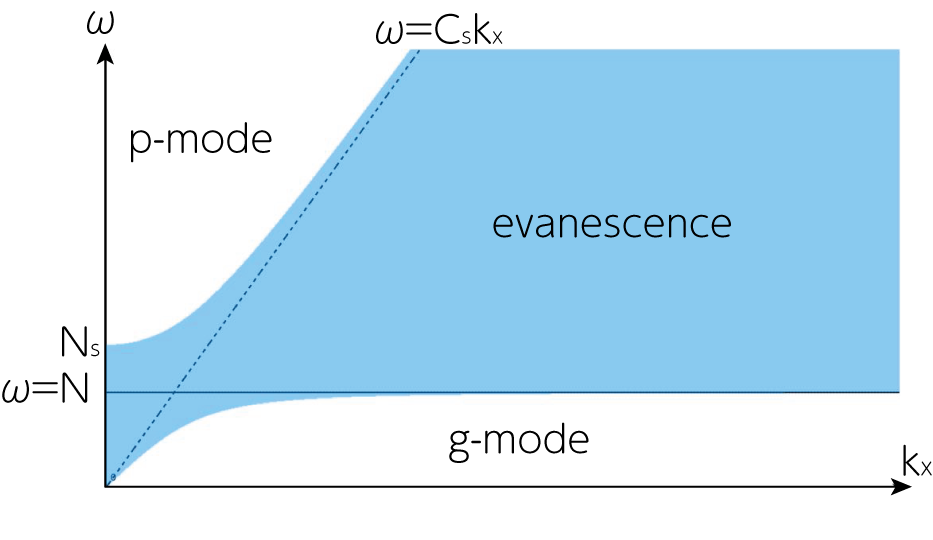
図中の色がついている領域はevanescence部と呼ばれ、波が伝播できない領域を指します。さらに\(\omega < N\)の領域がg-mode, そして\(\omega > N_s\)の領域がp-mode です。

\(k_x \gg 1\)のとき、(5)式の条件において等号が成り立つ場合を考えると

\[\begin{align} \omega^2 &= \frac{\left( k_x^2 + \frac{N_s^2}{C_s^2}\right) C_s^2 \pm \sqrt{\left( k_x^2 + \frac{N_s^2}{C_s^2}\right)^2 C_s^4 - 4 N^2 C_s^2 k_x^2}}{2} \simeq \frac{k_x^2 C_s^2 \pm \sqrt{k_x^4 C_s^4 - 4 N^2 C_s^2 k_x^2}}{2} \notag \\ &= k_x^2 C_s^2 \frac{1 \pm \sqrt{1-4 \frac{N^2}{k_x^2 C_s^2}}}{2} \simeq \frac{k_x^2 C_s^2}{2} \left\{ 1 \pm \left( 1- 2 \frac{N^2}{k_x^2 C_s^2}\right) \right\} \tag{6} \end{align}\]

\(N \ll k_x C_s\)を用いると\(\omega^2 \simeq k_x^2 C_s^2, N^2\)となります。よって許される振動数は\(\omega > k_x C_s, \omega < N\)となります。
\(k_x \ll 1\)のとき、(5)式の条件は

\[\omega^2 \simeq \frac{N_s^2 \pm \sqrt{N_s^4 - 4 N^2 C_s^2 k_x^2}}{2} = N_s^2 \frac{1 \pm \sqrt{1-4 \frac{N^2}{N_s^4} C_s^2 k_x^2}}{2} \simeq \frac{N_s^2}{2} \left\{ 1 \pm \left( 1- 2 \frac{N^2}{N_s^4}\right) \right\} \tag{7}\]

よって\(\omega^2 \simeq N_s^2, \frac{N^2}{N_s^2} k_x^2 C_s^2\)となります。よって許される振動数は\(\omega > N_s, \omega < (N/N_s) k_x C_s\)となります。\(k_x\)が小さいとき、p-modeは重力によって\(N_s\)以下で振動することができず、逆にg=modeは音波の圧縮性により\(k C_s\)以上で振動することが許されません。

参考文献

[1] Priest, “Solar Magnetohydrodynamics”
[2] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”
[3] 加藤正二, “天体物理学基礎理論”