Table of contents
GZKカットオフ
宇宙線スペクトルを見ると、\(10^{20} \mathrm{eV}\)あたりでさらにスペクトルが急激に落ちていることがわかります。
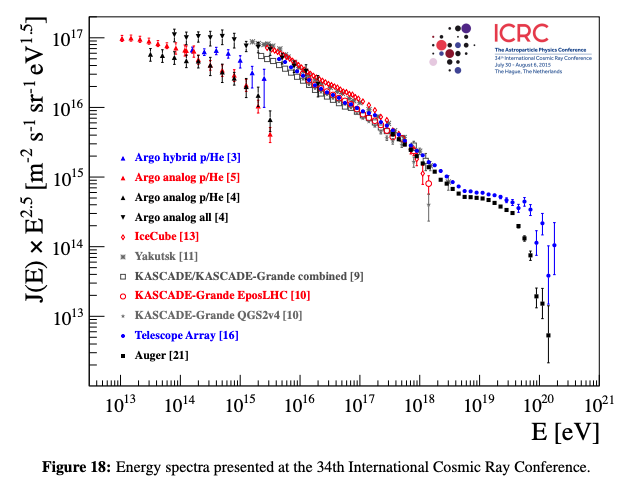
この現象は、これを最初に予想したGreisen, Zatsepin, Kuzminの3人の頭文字をとり、GZKカットオフなどと呼ばれます。 これは高エネルギー宇宙線のもととなる相対論的陽子が、宇宙に広く存在しているCMB光子と衝突しエネルギーを失うことで起こるとされています。 具体的には相対論的陽子は以下のような反応を起こします。
\[p + \gamma \rightarrow n + \pi^+ \tag{1}\]陽子が光子と衝突することで、中性子と荷電\(\pi\)中間子を生成するというものです。 さらに荷電\(\pi\)中間子は別の粒子に崩壊するため、この相対論的陽子が再び無限遠方に飛び去るということはありません。 今回はこのGZKカットオフを理解してみましょう。
CMB光子と相対論的陽子の衝突
ドップラーシフトを用いた導出
CMB光子の温度はおよそ\(3K\)とされています。 この温度の黒体放射の光子1個が持つエネルギーは、大雑把に
\[h \nu = k_B T \simeq \left( \frac{T}{10^4 \mathrm{K}}\right) \quad [\mathrm{eV}] \sim 3 \times 10^{-4} \quad [\mathrm{eV}] \tag{2}\]となります。 超相対論的な速度で運動する陽子\((\gamma \gg 1)\)の運動エネルギーは
\[T = m_p \gamma c^2 \tag{3}\]と書かれます。 今、これがCMB光子と正面衝突したとしましょう。 このとき、陽子静止系から見て衝突するCMB光子のエネルギーが\(\pi\)中間子の静止質量エネルギーである\(m_\pi c^2 \sim 150\mathrm{MeV}\)(より具体的には\(140 \mathrm{MeV}\))を越えてしまうと、(1)式の反応が起こります。 実験室系(相対論的陽子が運動して見える系、もしくはCMB光源静止系)での陽子の速度を\(v\)とし、陽子静止系でのCMB光子のエネルギーを\(E_\mathrm{CMB} = h\nu'\)としましょう。 陽子静止系に移ると、CMB光源が速度\(v\)で陽子に近づいてくると考えることができるため、ドップラーシフトを生じます。 このことから、(1)式の反応が起こる条件は
\[E_\mathrm{CMB} = h \nu' = h \nu \sqrt{\frac{c+v}{c-v}} \geq m_\pi c^2\tag{4}\]となります。 相対論的陽子の運動エネルギーの具体的な値を計算してみましょう。
\[\begin{align} &\sqrt{\frac{1+v/c}{1-v/c}} \geq \frac{m_\pi c^2}{h\nu} \ \Longrightarrow \ 1 + \frac{v}{c} \geq \underbrace{\left( \frac{m_\pi c^2}{h\nu}\right)^2}_{\equiv \eta} \left( 1- \frac{v}{c} \right) \ \Longrightarrow \ \frac{v}{c} \geq \frac{\eta -1}{\eta +1} \notag \\ &\Longrightarrow \ \gamma \geq \frac{1}{\sqrt{1-(v/c)^2}} = \frac{\eta + 1}{\sqrt{4\eta}} \tag{5} \end{align}\](2)式より、\(\eta \sim (50 \times 10^{10})^2\)と求まります。 さらに陽子の静止質量エネルギー\(m_p c^2 \sim 940 \mathrm{MeV}\)を代入すれば
\[T \geq \frac{\eta + 1}{\sqrt{4\eta}} m_p c^2 \sim 2.35 \times 10^{20} \quad [\mathrm{eV}] \tag{6}\]のように求まります。 このことから、この運動エネルギー以上の相対論的陽子は地球に飛来する前にCMB光子と反応を起こし、そのエネルギーを失います。 グラフの\(10^{20} \mathrm{eV}\)のあたりで急激にスペクトルが落ちていることを再現できました。
4元運動量を用いた導出
以下では4元運動量を用いて同じ結果になることを示してみましょう。 衝突前の超相対論的陽子とCMB光子の4元運動量をそれぞれ\(P_p^\mu, P_\gamma^\mu\)とおくと
\[c P_p^\mu = (E_p, c \mathbf{p}_p), \quad c P_\gamma^\mu = (E_\gamma, c \mathbf{p}_\gamma) \tag{7}\]のように書けます。 ここで\(E_p, E_\gamma\)はそれぞれ超相対論的陽子とCMB光子のエネルギー、そして\(\mathbf{p}_p, \mathbf{p}_\gamma\)はそれぞれ超相対論的陽子とCMB光子の3次元空間の運動量ベクトルです。 同様に、衝突後に生成された中性子と\(\pi\)中間子の4元運動量をそれぞれ\(P_n^\mu, P_\pi^\mu\)とすると
\[c P_n^\mu = (E_n, c \mathbf{p}_n), \quad c P_\pi^\mu = (E_\pi, c \mathbf{p}_\pi) \tag{8}\]のようになります。

衝突前の全系の4元運動量のスカラー積は
\[\begin{align} (cP_p^\mu + cP_\gamma^\mu)(cP_{p, \mu} + cP_{\gamma, \mu}) &= c^2 P_p^\mu P_{p, \mu} + c^2 \underbrace{P_\gamma^\mu P_{\gamma, \mu}}_{光子なので0} + 2 c^2 P_p^\mu P_{\gamma, \mu} \notag \\ &= - m_p^2 c^4 + 2 c^2 P_p^\mu P_{\gamma, \mu} \tag{9} \end{align}\]のように求まります。 同様に、衝突後の全系の4元運動量のスカラー積を考えましょう。 ここでは衝突により生成された中性子と\(\pi\)中間子の重心系で計算を行います。 すると\(\mathbf{p}_n + \mathbf{p}_\pi = \mathbf{0}\)より、重心に\(m_n + m_\pi\)の粒子が静止していると考えることができるため
\[(c P_n^\mu + c P_\pi^\mu) (c P_{n, \mu} + c P_{\pi, \mu}) = - (m_n + m_\pi)^2 c^4 \tag{10}\]と計算されます。 運動量保存から(9), (10)式での値が等しいことを用いると
\[- m_p^2 c^4 + 2 c^2 P_p^\mu P_{\gamma, \mu} = - (m_n + m_\pi)^2 c^4 \tag{11}\]です。 最後に、\(c^2 P_p^\mu P_{\gamma, \mu}\)を計算しましょう。 今、陽子は超相対論的速度で運動しているので\(E_p \simeq c \vert \mathbf{p}_p \vert = cp_p\)と考えるます。 さらに超相対論的陽子の運動方向を\(x\)軸正の方向に取れば
\[c P_p^\mu = (E_p, E_p, 0, 0) \tag{12}\]のように定めることができます。 この超相対論的陽子と正面衝突するCMB光子を考えると、そもそも光子においては\(E_\gamma = c \vert \mathbf{p}_\gamma \vert = cp_\gamma\)が成り立つので
\[c P_\gamma^\mu = (E_\gamma, -E_\gamma) \tag{13}\]となります。これでようやく
\[c^2 P_p^\mu P_{\gamma, \mu} = - E_p E_\gamma - E_p E_\gamma = -2 E_p E_\gamma \tag{14}\]と求まります。(11), (14)式より
\[- m_p^2 c^4 -4 E_p E_\gamma = - (m_n + m_\pi)^2 c^4 \ \Longrightarrow \ E_p = \frac{(m_n + m_\pi)^2 c^4 - m_p^2 c^4}{4 E_\gamma} \tag{16}\]を得ます。 ここに\(m_n c^2 \sim 940 \mathrm{MeV}, m_p c^2 \sim 938 \mathrm{MeV}, m_\pi c^2 \sim 150 \mathrm{MeV}\)、そして\(E_\gamma \sim 3 \times 10^4 \mathrm{eV}\)を代入すれば
\[E_p \sim 2.6 \times 10^{20} \quad [\mathrm{eV}] \tag{17}\]のようになります。ドップラー効果を用いて求めた値(6)と同じオーダーの結果を得ることができました。
相対論的陽子の平均自由行程
実は先程の相対論的陽子とCMB光子との衝突には、\(\sigma \sim 0.25 \mathrm{mb}\)という反応断面積が求められています。 ここで\(1 \mathrm{mb} = 10^{-3} \times 10^{-24} \mathrm{cm}^2\)で、\(\mathrm{b}\)は原子核などの断面積を表すバーンと呼ばれる単位です。 この値とCMB光子の個数密度\(n_\mathrm{CMB} \sim 411 \mathrm{cm}^{-3}\)という値から、この衝突反応における相対論的陽子の平均自由行程を計算することができます。
\[\ell = \frac{1}{n_\mathrm{CMB} \sigma} \sim \frac{1}{411 \mathrm{cm}^{-3} \times 0.25 \times 10^{-27} \mathrm{cm}^2} \sim 1.0 \times 10^{25} \quad [\mathrm{cm}] \sim 3.0 \quad [\mathrm{Mpc}] \tag{18}\]この計算から、超相対論的陽子は実はたった3Mpcの範囲しか到達することができません。 すなわち、もしこれ以上の宇宙線が観測されたなら、それは比較的近傍の天体を発生源とするものであると考えることができます。
参考文献
[1] FAST Project website
[2] Verze, 2016, “Cosmic rays: air showers from low to high energies”