Table of contents
ジッター放射 (jitter radiation)
相対論的電子が一様磁場中を運動すると、その軌道は円運動となります。 また相対論的ビーミング効果も合間って、この荷電粒子からの放射はシンクトロン放射になることが知られています。 しかし、例えばガンマ線バースト(GRB)の衝撃波面では一様ではなく、乱れた電磁場が存在するとされています。 今回は、その乱れた電磁場(小さいスケールで磁場の向きが変化する場合)での、相対論的電子からの放射について考えましょう。
軌道のずれ角と問題設定
磁場が\(+z\)方向と\(-z\)方向に、頻繁にその向きを変化させている領域中を、相対論的電子が運動することを考えましょう。 一様磁場中での相対論的電子の円運動のラーモア半径は
\[r_L = \frac{m_e c^2 \gamma \beta}{e B} \underbrace{\simeq}_{\beta \sim 1} \frac{m_e c^2 \gamma}{e B} \tag{1}\]です。 ここで、電子の運動が超相対論的であるとして\(v \sim c (\beta \sim 1)\)のように近似しました。 また超相対論的な場合、電子の運動量は\(p \simeq m_e c \gamma\)と書けます。 そして磁場の典型的な相関スケール、すなわち磁場が同じ方向に揃っている距離を\(\lambda_B\)としましょう。 この距離を電子が移動するのにかかる時間は\(t \simeq \lambda_B / c\)です。 この間に電子は磁場からローレンツ力\(F_L\)を受けます。 よってローレンツ力によりこの電子にもたらされる垂直方向の力積(=運動量変化)は
\[p_\perp \simeq F_L t \simeq \frac{e B \lambda_B}{c} \tag{2}\]のように計算できます。 ここから、下図のように定義される、観測者視線方向からの電子の軌道のずれ角\(\alpha\)は
\[\alpha \simeq \frac{p_\perp}{p} \simeq \frac{eB \lambda_B}{m_e c^2 \gamma} \tag{3}\]のようになります。 ここで、相対論的ビーミングの放射コーンの角度\(\Delta \theta \simeq 1 / \gamma\)とこの比を\(\delta\)と定義しましょう。 すると
\[\delta \equiv \frac{\alpha}{\Delta \theta} = \frac{eB \lambda_B}{m_e c^2} \underbrace{=}_{(1)} \frac{\gamma \lambda_B}{r_L} \simeq \frac{\gamma }{k_B r_L}\tag{4}\](4)式の途中式からわかるように、\(\delta\)は\(B, \lambda_B\)にしか依存しません。 またさらに扱いやすいように、最後の変形では\(\lambda_B \simeq k_B^{-1}\)のように波数を用いて表現をしました。
さて、ここからは具体的にスペクトルを求める問題設定を考えていきましょう。 軌道のズレが非常に小さい場合、観測者は放射コーンを常に見続けることになります。 これにより、シンクロトロン放射とは違ったスペクトルが観測されるはずです。
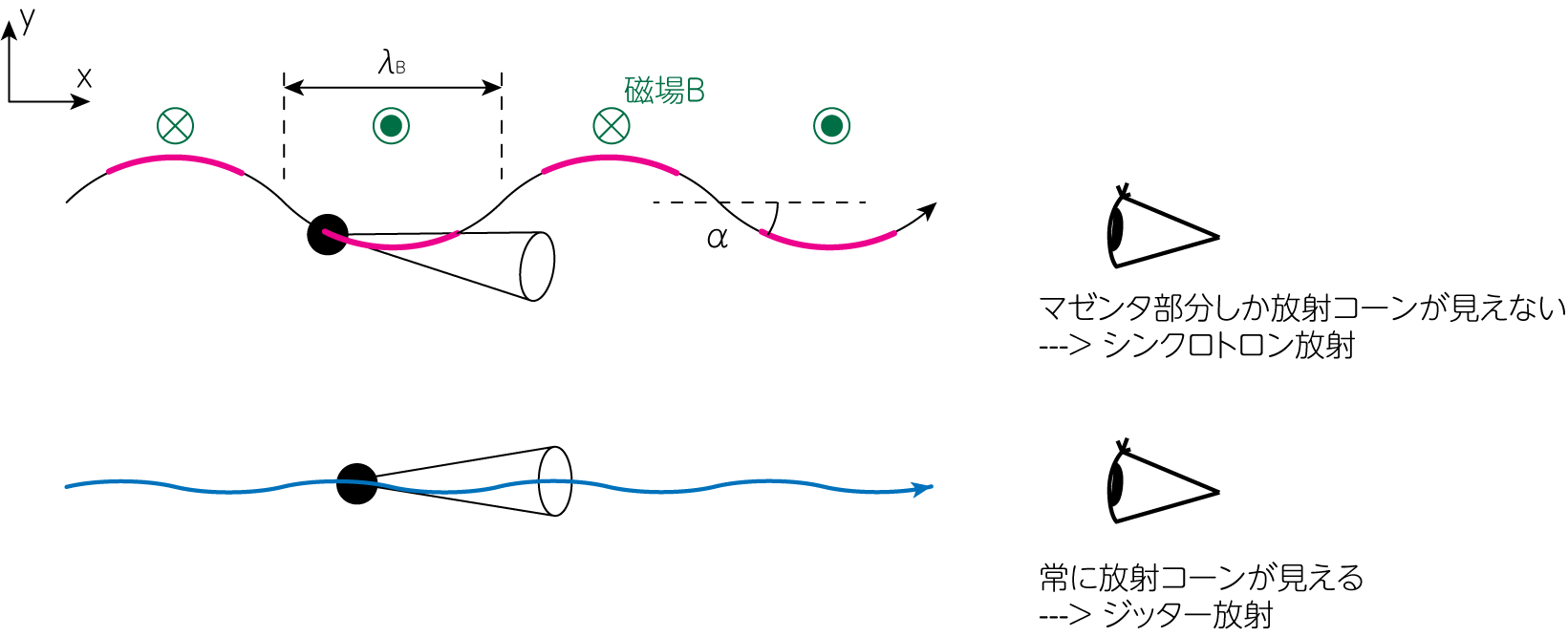
この議論から、今回扱う問題は\(\delta \ll 1\)のような状況であるとわかります。 このように「細かく振動する(jittering)ような軌道からの放射」という意味をこめて、これをジッター放射(jitter radiation)と呼びます。
スペクトル導出
それではスペクトルを導出していきましょう。 超相対論的電子が出す放射の電場は、輻射場のフーリエスペクトルより
\[\hat{\mathbf{E}}(\mathbf{r}, \omega) = \frac{-e}{2\pi c^2 R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \frac{\mathbf{n} \times \{(\mathbf{n} - \boldsymbol{\beta}) \times \hat{\mathbf{a}}_{\omega'}\}}{\kappa^2} \tag{5}\]です。 ここで\(\kappa = 1 -\mathbf{n} \cdot \boldsymbol{\beta}, \hat{\mathbf{a}}_{\omega'} = \int_{-\infty}^\infty \mathbf{a} e^{i\omega' t} dt\)です。 また\(\omega' = \omega (1-\frac{\mathbf{r}_0 \cdot \mathbf{n}}{ct'})\)ですが、以降では電子の運動は等速直線運動であると考えて\(\omega' = \omega (1 - \frac{\mathbf{v} \cdot \mathbf{n}}{c}) = \omega \kappa\)であるとします。 これより、単位立体角・単位周波数あたりの放射エネルギーは
\[\frac{dW}{d\omega d\Omega} = c R^2 \vert \hat{\mathbf{E}} (\omega) \vert^2 = \frac{e^2}{4\pi^2 c^3} \frac{\vert \mathbf{n} \times \{(\mathbf{n} - \boldsymbol{\beta}) \times \hat{\mathbf{a}}_{\omega'}\} \vert^2 }{\kappa^4} = \frac{e^2}{4\pi^2 c^3} \left( \frac{\omega}{\omega'} \right)^4 \left| \mathbf{n} \times \left\{ \left( \mathbf{n} - \boldsymbol{\beta} \right) \times \hat{\mathbf{a}}_{\omega'} \right\} \right|^2 \tag{6}\]のようになります。 これを全立体角で積分します。 計算にあたり、近似を施しましょう。 \(\mathbf{n} \cdot \boldsymbol{\beta} = \frac{v}{c} \cos \theta\)のように、\(\mathbf{n}\)と\(\mathbf{v}\)の成す角度を\(\theta\)とします。 このとき\(\theta \simeq \Delta \theta \ll 1\)で十分に小さいとすると
\[\begin{align} \kappa &= 1 - \frac{v}{c} \cos \theta \simeq 1 - \frac{v}{c} \left( 1 - \frac{\theta^2}{2}\right) \underbrace{\simeq}_{v/c \sim 1} 1 - \frac{v}{c} + \frac{\theta^2}{2} \simeq \frac{1}{2} \left\{ 2 \left( 1 - \frac{v}{c} \right) + \theta^2 \right\} \notag \\ &\underbrace{\simeq}_{1+\frac{v}{c} \sim 2} \frac{1}{2} \left\{ \left( 1 + \frac{v}{c} \right) \left( 1 - \frac{v}{c} \right) + \theta^2 \right\} = \frac{1}{2} \left( 1 - \frac{v^2}{c^2} + \theta^2 \right) = \frac{1}{2} (\gamma^{-2} + \theta^2) \tag{7} \end{align}\]のように近似することができます。 以上より
\[\omega' = \omega \kappa \ \Longrightarrow \ d\omega' = \omega \theta d\theta \tag{8}\]を得ます。 これを用いれば、全立体角積分は\(d\Omega = \sin \theta d\theta d\phi \simeq \theta d\theta d\phi = d\phi d\omega' / \omega\)のように変数変換されます。 積分範囲は\(\theta: 0 \rightarrow \pi\)から\(\omega': \omega/2\gamma^2 \rightarrow \omega (\gamma^{-2} + \pi^2) / 2\)となりますが、相対論的ビーミング効果から\(\theta\)が大きな部分での寄与はゼロとなるはずです。 したがって、積分範囲の上限は無限大にしても差し支えありません。 よって
\[\begin{align} \frac{dW}{d\omega} &= \frac{e^2}{2\pi c^3} \int_{\omega / 2\gamma^2}^\infty \left( \frac{\omega}{\omega'} \right)^4 \left| (\mathbf{n} \cdot \hat{\mathbf{a}}_{\omega'}) \mathbf{n} - \hat{\mathbf{a}}_{\omega'} - (\mathbf{n} \cdot \hat{\mathbf{a}}_{\omega'}) \boldsymbol{\beta} + (\mathbf{n} \cdot \boldsymbol{\beta}) \hat{\mathbf{a}}_{\omega'} \right|^2 \frac{d\omega'}{\omega} \notag \\ &= \frac{e^2 \omega^3}{2\pi c^3} \int_{\omega / 2\gamma^2}^\infty \frac{\vert \hat{\mathbf{a}}_{\omega'} \vert^2}{\omega'^4} \left| 1 - \mathbf{n} \cdot \boldsymbol{\beta} \right|^2 d\omega' \tag{9} \end{align}\]のようになります。 ここで軌道はほぼ直線で、電子にかかる加速度は常に垂直である(\(\mathbf{n} \cdot \hat{\mathbf{a}} \sim 0\))という近似を用いました。 さらに
\[\mathbf{n} \cdot \boldsymbol{\beta} = \beta \cos \theta \simeq \beta \left( 1 - \frac{\theta^2}{2}\right) \underbrace{\simeq}_{(7)} \beta \left( 1 - \frac{\omega'}{\omega} + \frac{1}{2\gamma^2}\right) \tag{10}\]のような近似を行い、ここに\(\beta \sim 1\)を代入すれば
\[\left| 1 - \mathbf{n} \cdot \boldsymbol{\beta} \right|^2 \simeq \left( -\frac{\omega'}{\omega} + \frac{1}{2\gamma^2} \right)^2 = \frac{\omega'^2}{\omega^2} - \frac{\omega'}{\omega \gamma^2} + \frac{1}{4\gamma^4} \tag{11}\]となります。最終的に
\[\frac{dW}{d\omega} = \frac{e^2 \omega}{2\pi c^3} \int_{\omega/ 2\gamma^2}^\infty \frac{\vert \hat{\mathbf{a}}_{\omega'} \vert^2}{\omega'^2} \left( 1 - \frac{\omega}{\omega' \gamma^2} + \frac{\omega^2}{4 \omega'^2 \gamma^4}\right) d\omega' \tag{12}\]を得ます。 第一項は電子軌道の微小な振動によるもの、第二・第三項は相対論的ビーミングと組み合わさった輻射場の角度構造に起因する補正です。
ランダウ・リフシッツなどの文献では、第三項の分母が2になる...近似の仕方にミス(?_?)
べき乗分布磁場でのスペクトル計算
(12)式に磁場の情報、そしてそこから計算される加速度を代入すれば、スペクトルが求まります。 軌道のずれ角と問題設定での図より、今の問題設定では\(\mathbf{v} \simeq c \mathbf{e}_x, \mathbf{B} = B \mathbf{e}_z, \dot{\mathbf{p}} = m_e \gamma a \mathbf{e}_y\)のようでした。 これらより
\[m_e \gamma a \mathbf{e}_y = \frac{-e}{c} \mathbf{v} \times \mathbf{B} \ \Longrightarrow \ a = \frac{eB}{m_e \gamma} \tag{13}\]のように加速度が求まります。 (12)式で用いられているのは、加速度をフーリエ変換したものです。 よって、スペクトル計算に必要となるのは
\[\hat{a}_{\omega'} = \frac{e \hat{B}_{\omega'}}{m_e \gamma} = \frac{e \hat{B}_{k'}}{m_e c \gamma} \tag{14}\]です。 あとは磁場の空間分布をフーリエ変換した\(\hat{B}_{k'}\)を入れれば良いことがわかります。 一般的なものとして、磁場強度の2乗(すなわち磁場のエネルギー)の空間分布が
\[\hat{B}_k^2 = C_k k^{-\mu} \tag{15}\]のようにべき乗で与えられるとしましょう。 ここで\(\mu\)は正の数であるとします。 さらに電子の運動が超相対論的であるとして、(12)式の第二・第三項は無視すると
\[\frac{dW}{d\omega} \simeq \frac{e^2 \omega}{2\pi c^3} \int_{\omega / 2\gamma^2}^\infty \frac{e^2}{m_e^2 c^2 \gamma^2} \frac{\hat{B}_{k'}^2}{\omega'^2} d\omega' \underbrace{=}_{\omega' = c k'} \frac{e^4 \omega}{2 \pi m_e^2 c^5 \gamma^2} \int_{\omega / 2\gamma^2}^\infty \frac{C_k c^\mu \omega'^{-\mu}}{\omega'^2} d\omega' \propto \omega^{-\mu} \tag{16}\]のようになります。 すなわちジッター放射のスペクトルは、その超相対論的電子が通過してきた磁場分布をそのまま反映していることがわかります。 これは、トムソン散乱では入射電磁波と散乱電磁波の振動数が同じになるように、電子は乱れた電磁場の周波数に対応した電磁波を放射していることから理解できます。
定性的な導出
ここまではなるべく厳密に数式を変形することでスペクトルの導出を行いましたが、ざっくりとした考えからジッター放射スペクトルを導出してみましょう。 超相対論的な電子が乱れた電磁場中を運動すると、電子静止系でこれを見ることにします。 すると電子の速度は\(v \sim c\)のため、電子静止系では乱れた電磁場が電子に向かって光速度\(c\)で向かってくることになります。 つまり、これは仮想的なパルス状の電磁波(光子)であると解釈することができ、この仮想光子を逆コンプトン散乱する現象である、と考えることができます。
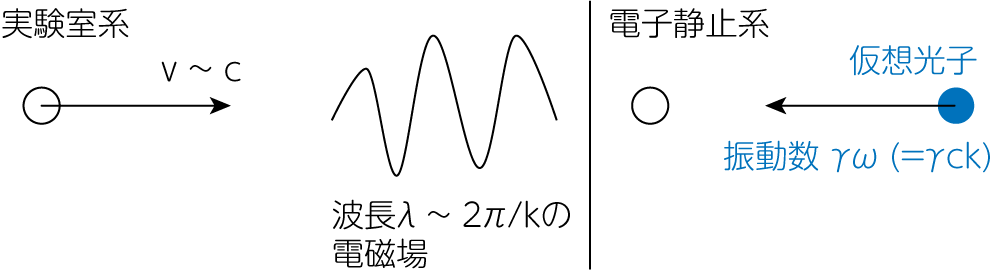
振動数\(\omega = ck\)の光子がローレンツ変換により、電子静止系では\(\gamma \omega\)となります。 さらにそれを正面に跳ね返すことを考え、再び実験室系にローレンツ変換すると、散乱後の光子の振動数は\(\gamma^2 \omega\)となります。 トムソン散乱を例に出して説明したように、電子は乱れた電磁場の周波数に対応した放射を出していることがわかります。
γ線バーストや宇宙ジェットへの応用
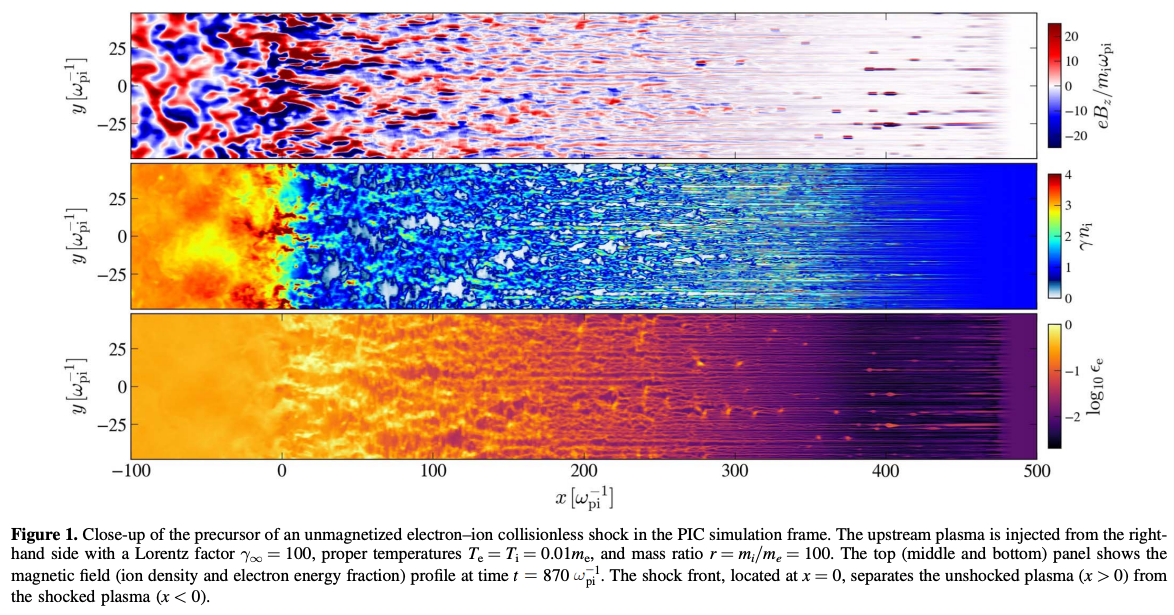
γ線バーストや宇宙ジェットは、磁場が関係する宇宙現象としてよく知られています。 しかしシンクロトロン放射では再現できないスペクトルがあり、その説明としてジッター放射が研究されてきました。 γ線バーストや宇宙ジェットで形成される衝撃波面では、ワイベル不安定性(Weibel instability)と呼ばれる磁場生成機構が働いていると考えられています。 これによりできた乱流電磁場中を、衝撃波面で生成された超相対論的電子が駆け抜けることで、ジッター放射が起こるだろうとされています。 上述のスペクトル導出の議論は、超相対論的電子がほぼ直線軌道を描くという近似の下で導出されたものでした。
しかし、シンクロトロン放射とジッター放射の間のような軌道を描く場合、その電子に対しては直線近似を適用することはできません。 ジッター放射だけでは説明できない現象が、γ線バーストや宇宙ジェットにはまだまだ隠れているのです。
参考文献
[1] Medvedev, 2000, “Theory of “Jitter” Radiation from Small-Scale Random Magnetic Fields and Prompt Emission from Gamma-Ray Burst Shocks”
[2] Workman et al., 2008, “Jitter radiation in gamma-ray bursts and their afterglows: emission and self-absorption”
[3] Vanthieghem et al., 2022, “Origin of Intense Electron Heating in Relativistic Blast Waves”
[4] Dermer & Menon, “High Energy Radiation from Black Holes: Gamma Rays, Cosmic Rays and Neutrinos”
[5] ランダウ & リフシッツ, “場の古典論”
[6] 中村文隆, 鶴剛, 長田哲也, 藤沢健太, 梅村雅之, 福江純, “放射素過程の基礎”
[7] 寺木悠人, 修士論文, “乱れた磁場中を運動する相対論的粒子からの放射”
[8] 寺木悠人, “乱れた電磁場中を運動する相対論的電子からの放射”