Table of contents
クリーク被覆問題 (Clique cover problem)
ここではクリーク被覆問題の定式化について、忘れないようにメモしておきます。
概要
この問題は、あるグラフが与えられたときに何個のクリーク(完全グラフ)に分割されるかを考える問題です。この問題はNP完全として知られます。
完全グラフ
完全グラフ(complete graph)とは、異なる2点が全て隣接しているグラフ構造のことです。ただしループや多重辺は含みません。以下は頂点数4の完全グラフの例です。
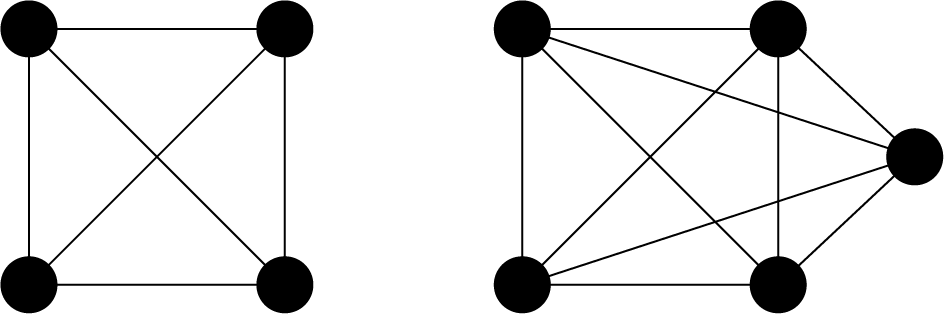
頂点数\(N\)の完全グラフは、数学記号で\(K_N\)と表されます。
\(K_N\)はそこに含まれる2点を選んだときに、その2点が必ず辺で結ばれているような構造を持ちます。すると辺の数は\(N\)個の頂点から2つを選ぶ組合せの数\({}_N C_2 = \frac{1}{2} N (N-1)\)だけあることがわかります。
数理モデル
(量子)アニーリングで最適化問題を解くためには、数理モデルが必要です。ここでは以下の考え方から、クリーク被覆問題を数式で表すことを考えます。
バイナリ変数
頂点\(v\)が\(c\)番目のクリークに属するとき\(x_{v, c} = 1\)、そうでないとき\(x_{v, c}=0\)となるような[0, 1]のバイナリ変数\(x_{v, c}\)を考えます。クリークに分ける操作を、頂点を塗り分ける操作と考えた方がイメージが掴みやすいかもしれません。
制約: 1つの頂点は1つの色しか選択できない
これを数式で表現すると
\[\sum_{c=0}^{C-1} x_{v, c} = 1 \quad (\forall v) \tag{2}\]ここで\(C\)は、塗り分けたい色の総数です。
目的関数: 完全グラフからの差を最小化する
色\(c\)に塗り分けられた部分の頂点数を\(N_c(=\sum_{v} x_{v, c})\)とすると、この頂点たちが完全グラフを形成しているなら、その辺の数は\(\frac{1}{2} N_c (N_c -1)\)となります。しかし、色\(c\)に塗り分けられた頂点が形成する実際の辺の数は\(\sum_{(i, j) \in E} x_{i, c} x_{j, c}\)で表されます。\(E\)はグラフに存在する辺の集合です。今の問題設定から、色\(c\)に塗り分けられた頂点はなるべく完全グラフを形成してほしいため、この差が0に近いほど綺麗にグラフがクリークに分けられていることになります。よって目的関数を
\[\mathrm{obj} = \sum_{c=0}^{C-1} \left\{ \frac{1}{2} \left( \sum_{v =0}^{V-1} x_{v, c}\right) \left( \sum_{v =0}^{V-1} x_{v, c} -1 \right) - \sum_{(i, j) \in E} x_{i, c} x_{j, c} \right\} \tag{3}\]のように定めます。ここで\(V\)は考えているグラフの頂点数です。
ハミルトニアン
(2), (3)式から、この最適化問題のQUBOハミルトニアンは
\[H = \mathrm{obj} + \lambda \sum_{v=0}^{V-1} \left( \sum_{c=0}^{C-1} x_{v, c} -1\right)^2 \tag{4}\]ここで\(\lambda\)は(2)式の制約の重みを表す定数(未定乗数)です。
参考文献
[1] Lucas, 2014, “Ising formulations of many NP problems”
[2] T-Wave website, “クリーク被覆問題をD-Waveマシンで解く”