点源爆発の自己相似解 (Sedov-Taylor solution)

点源爆発の自己相似解のことをSedov-Taylor解と呼び、厳密解が知られています。中心から爆発によって供給された高音・高圧のガスは周りの低温のガスをかき集めながら膨張します。形成された衝撃波は、衝撃波でのジャンプ条件(ランキン・ユゴニオ条件)を満たしながら広がっていきます。

球対称での基礎方程式

球対称なので\(\frac{\partial}{\partial \theta} = \frac{\partial}{\partial \varphi} = 0, v_\theta = v_\varphi = 0\)とします。すると基礎方程式は

\[\frac{\partial \rho}{\partial t} + \frac{1}{r^2} \frac{\partial }{\partial r}(r^2 \rho v_r) = 0\] \[\frac{\partial v}{\partial t} + v \frac{\partial v}{\partial r} + \frac{1}{\rho}\frac{\partial p}{\partial r} = 0\] \[\frac{\partial }{\partial t}\left(\frac{p}{\rho^\gamma} \right) + v_r \frac{\partial }{\partial r} \left(\frac{p}{\rho^\gamma}\right) = 0\]

のように書くことができます。

相似解を求める

最初から相似解を用いた解を模索します。無次元量\(\xi\)を

\[\xi = A r^a t^b \tag{1}\]

と定義し、\(\rho, v_r, p\)が\(\xi\)のみに依存する解を求めます。解の境界(爆風の衝撃波面)の位置を\(R(t)\)とすると

\[\xi_0 = A (R(t))^a t^b\]

を衝撃波面の位置を表すものとして導入します。さらにパラメータとして\(\lambda = \xi / \xi_0\)を導入します。爆風の通過した範囲は\(\lambda = 0\sim 1\)になっているはずです。
方程式を無次元化しましょう。\(\rho, v_r, p\)の無次元量として\(\rho^\ast, v_r^\ast, p^\ast\)とすると

\[v_r = v^\ast \frac{r}{t}, \ \rho = \rho^\ast \rho_0, \ p = p^\ast \rho_0 \left( \frac{r}{t}\right)^2\]

となります。偏微分はそれぞれ

\[\frac{\partial }{\partial t} = \frac{\partial \lambda}{\partial t} \frac{\partial }{\partial \lambda} = \frac{b\lambda}{t} \frac{\partial }{\partial \lambda}\] \[\frac{\partial }{\partial r} = \frac{\partial \lambda}{\partial r} \frac{\partial }{\partial \lambda} = \frac{a \lambda}{r} \frac{\partial }{\partial \lambda}\]

のように書き換えられます。

連続の式より

\[\begin{align} &\frac{\partial \rho_0 \rho^\ast}{\partial t} + \frac{1}{r^2} \frac{\partial }{\partial r} \left( r^2 \rho_0 \rho^\ast \frac{r}{t} v_r^\ast \right) = 0 \notag \\ &\Longrightarrow \ \frac{\partial \rho^\ast}{\partial t} + \frac{1}{r^2 t} \frac{\partial }{\partial r} (\rho^\ast v_r^\ast r^3 = \frac{\partial \rho^\ast}{\partial t} + \frac{1}{r^2 t} \left( 3r^2\rho^\ast v_r^\ast + r^3 v_r^\ast + r^3 \rho^\ast \frac{\partial v_r^\ast}{\partial r} \right) = 0 \notag \\ &\Longrightarrow \ \frac{b\lambda}{t} \frac{\partial \rho^\ast}{\partial \lambda} + \frac{3\rho^\ast v_r^\ast}{t} + \frac{r v_r^\ast}{t} \frac{a\lambda}{r} \frac{\partial \rho^\ast}{\partial \lambda} + \frac{r\rho^\ast}{t} \frac{a \lambda}{r} \frac{\partial v_r^\ast}{\partial \lambda} = 0 \notag \\ &\Longrightarrow \ 3v_r^\ast + (b+av_r^\ast) \frac{\partial \ln \rho^\ast}{\partial \ln \lambda} + a\frac{\partial v_r^\ast}{\partial \ln \lambda} \notag \end{align}\]

運動方程式より

\[\begin{align} &\frac{\partial }{\partial t} \left(v_r^\ast \frac{r}{t} \right) + v_r^\ast \frac{r}{t} \frac{\partial }{\partial r} \left( v_r^\ast \frac{r}{t} \right) + \frac{1}{\rho_0 \rho^\ast} \frac{\partial }{\partial r} \left( p^\ast \rho_0 \frac{r^2}{t^2}\right) \notag \\ &= -\frac{v_r^\ast r}{t^2} + \frac{r}{t} \frac{\partial v_r^\ast}{\partial t} + \frac{r v_r^{\ast 2}}{t^2} + \frac{v_r^\ast r^2}{t^2} \frac{\partial v_r^\ast}{\partial r} + \frac{r^2}{\rho^\ast t^2} \frac{\partial p^\ast}{\partial r} + \frac{2r}{\rho^\ast t^2} p^\ast = 0 \notag \\ &\Longrightarrow \ -v^\ast + b\lambda \frac{\partial v_r^\ast}{\partial \lambda} + v_r^{\ast 2}+ v_r^\ast a \lambda \frac{\partial v_r^\ast}{\partial \lambda} + \frac{a\lambda}{\rho^\ast} \frac{\partial p^\ast}{\partial \lambda} + \frac{2p^\ast}{\rho^\ast} = 0 \notag \\ &\Longrightarrow \ v_r^\ast (v_r^\ast -1) + (b+av_r^\ast) \frac{\partial v_r^\ast}{\partial \ln \lambda} + \frac{2p^\ast}{\rho^\ast} + \frac{a}{\rho^\ast} \frac{\partial p^\ast}{\partial \ln \lambda} \notag \end{align}\]

エネルギー方程式より

\[\begin{align} &\frac{\partial }{\partial t} \left( \frac{p}{\rho^\gamma} \right) + v_r \frac{\partial }{\partial r} \left(\frac{p}{\rho^\gamma} \right) = \frac{\partial }{\partial t} \left(\frac{p^\ast rho_0 r^2 / t^2}{\rho^{\ast \gamma} \rho_0^\gamma }\right) + v_r^\ast \frac{r}{t} \frac{\partial }{\partial r} \left( \frac{p^\ast \rho_0 r^2/t^2}{\rho^{\ast \gamma} \rho_0^\gamma}\right) \notag \\ &= \frac{\rho_0 r^2}{\rho_0^\gamma} \left\{ \frac{-2}{t^3} \frac{p^\ast}{\rho^{\ast \gamma}} + \frac{1}{t^2} \frac{\partial }{\partial t} \left(\frac{p^\ast}{\rho^{\ast \gamma}} \right)\right\} + \frac{\rho_0}{\rho_0^\gamma} v_r^\ast \frac{r}{t^3} \left\{ 2r\frac{p}{\rho^{\ast \gamma}} + r^2 \frac{\partial }{\partial r} \left(\frac{p^\ast}{\rho^{\ast \gamma}} \right)\right\} = 0 \notag \\ &\Longrightarrow \ -2 \frac{p^\ast}{\rho^{\ast \gamma}} + b\lambda \frac{\partial }{\partial \lambda} \left( \frac{p^\ast}{\rho^{\ast \gamma}} \right) + v_r^\ast \left(\frac{2p^\ast}{\rho^{\ast \gamma}} + a\lambda \frac{\partial }{\partial \lambda} \left( \frac{p^\ast}{\rho^{\ast \gamma}} \right) \right)= 0 \notag \\ &\Longrightarrow \ 2(v_r^\ast -1)\frac{p^\ast}{\rho^{\ast \gamma}} + \frac{b\lambda}{\rho^{\ast \gamma}} \frac{\partial p^\ast}{\partial \lambda} + b\lambda (-\gamma) \rho^{\ast, -\gamma-1} \frac{\partial \rho^\ast}{\partial \lambda} + a\lambda v_r^\ast \frac{1}{\rho^{\ast \gamma}} \frac{\partial p^\ast}{\partial \lambda} + a\lambda v_r^\ast p^\ast (-\gamma) \rho^{\ast, -\gamma-1} \frac{\partial \rho^\ast}{\partial \lambda} = 0 \notag \\ &\Longrightarrow \ 2(v_r^\ast -1) + (b+av_r^\ast) \frac{\partial ln p^\ast}{\partial \ln \lambda} -\gamma (b+av_r^\ast) \frac{\partial \ln \rho^\ast}{\partial \ln \lambda} = 0 \notag \end{align}\]

これらの微分方程式を境界条件のもとで解けば良いことがわかります。しかし、これを解くことは難しいので、特徴のある量だけを取り出して説明することにしましょう。
独立変数\(r, t\)と系のパラメータ\(\rho_0, E_0\)から無次元量を作ります。

\[\xi = \rho_0^\alpha E_0^\beta r^\gamma t^\delta\]

この式の単位は\({\rm g}^{\alpha}{\rm cm}^{-3\alpha}{\rm g}^{\beta}{\rm cm}^{2\beta} {\rm s}^{-2\beta} {\rm cm}^{\gamma} {\rm s}^{\delta}\)より

\[\left\{ \begin{array}{ll} \alpha + \beta = 0\\ -3\alpha + 2\beta + \gamma = 0 \\ -2\beta + \delta = 0 \end{array} \right. \ \Longrightarrow \ \alpha = \frac{1}{5} \gamma, \ \beta = -\frac{1}{5} \gamma , \ \delta = -\frac{2}{5} \gamma\]

\(\gamma=1\)とすると

\[\xi = \left(\frac{\rho_0}{E_0}\right)^{1/5} r t^{-2/5}\]

(1)式と比較すると

\[a = 1, \ b= -\frac{2}{5} , \ A = \left(\frac{\rho_0}{E_0}\right)^{1/5}\]

よって衝撃波の半径は

\[R(t) = \xi_0 \left(\frac{\rho_0}{E_0}\right)^{1/5} t^{2/5}\]

そしてその膨張速度は

\[D(t) = \frac{dR}{dt} = \frac{2}{5} \xi_0 \left(\frac{\rho_0}{E_0}\right)^{1/5} t^{-3/5} = \frac{2}{5} \frac{R(t)}{t}\]

また、衝撃波面\(R(t) (\lambda=1)\)におけるランキン・ユゴニオの関係式より

\[\rho_1 = \frac{\gamma + 1}{\gamma-1}\rho_0\] \[v_1 = D(t) - \frac{\gamma - 1}{\gamma+1} D(t) = \frac{2}{\gamma+1} D(t) = \frac{4}{5} \frac{1}{\gamma + 1} \xi_0 \left(\frac{\rho_0}{E_0}\right)^{1/5} t^{-3/5}\] \[p_1 = \frac{2}{\gamma +1} \rho_0 D^2(t) = \frac{8}{25} \frac{\rho_0}{\gamma +1}\xi_0^2 \left(\frac{\rho_0}{E_0}\right)^{2/5} t^{-6/5}\]

などを得ます。

数値計算

最後に数値計算から得られる各物理量の分布を示します。

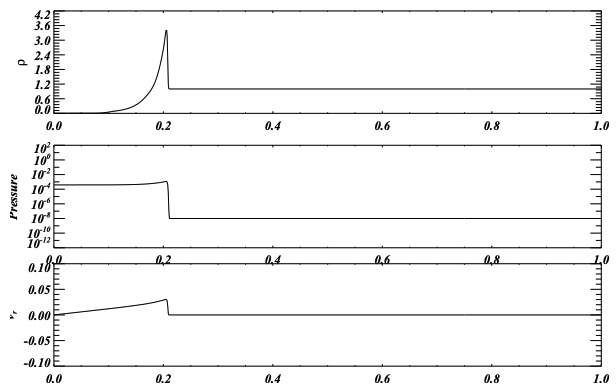上から順に密度・圧力・動径方向の速度分布上から順に、密度、圧力、動径方向の速度分布図。