Table of contents
偏光
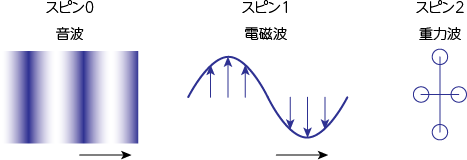
ベクトル波とスピン
電磁波はその電場または磁場成分を指定すれうばその物理状態が指定されます。物質にエネルギーを伝えるのは電場成分であるため、通常は電場のみを扱います。
電場は進行方向に垂直な面内のベクトルです。ここで「ベクトルである」という厳密な意味は「進行方向を軸として座標を一回転させると、一回だけ元に戻る」ということにより定義されます。したがって電磁波はベクトルであると言えます。これをスピンが1である、というように呼びます。
他にもスピン2の例としては重力波が挙げられます。これはベクトルではなくテンソルです。スピン0は例外で、任意の無限小回転に対して不変なもの、すなわち一回転させると無限回元に戻るものを意味します。このような波動をスカラーと呼びます。音波などの縦波がその例です。
以下は電磁波のベクトル性を反映した物理量である、偏光状態についてメモしたものです。
単色電磁波の偏光状態
角振動数\(\omega\)の偏光状態について調べてみましょう。ここで電磁波の進行方向を\(z\)軸に取ります。その位相を\(\tau=\omega t - kz\)と表すと、任意の電磁波の電場成分は以下のように書けます。
\[\left\{ \begin{array}{c} E_x = a_1 \cos (\tau + \delta_1) \\ E_y = a_2 \cos (\tau + \delta_2) \end{array} \right.\]\(\cos (\tau + \delta_1) = \cos \tau \cos \delta_1 - \sin \tau \sin \delta_1\)などより、上式の2つの電場を
\[\left( \begin{array}{c} \frac{E_x}{a_1} \\ \frac{E_y}{a_2} \end{array} \right) = \left( \begin{array}{cc} \cos \delta_1 & - \sin \delta_1 \\ \cos \delta_2 & - \sin \delta_2 \end{array} \right) \left( \begin{array}{c} \cos \tau \\ \sin \tau \end{array} \right) \tag{1}\]のように行列を用いた1つの式にまとめて書くことができます。このとき、(1)式に現れた行列を\(A\)とすると、その逆行列は
\[A^{-1} =\frac{1}{-\cos\delta_1\sin\delta_2 + \cos \delta_2 \sin\delta_1} \left( \begin{array}{cc} -\sin \delta_2 & \sin \delta_1 \\ -\cos \delta_2 & \cos \delta_1 \end{array} \right) =\frac{1}{\sin \delta} \left( \begin{array}{cc} -\sin \delta_2 & \sin \delta_1 \\ -\cos \delta_2 & \cos \delta_1 \end{array} \right) \tag{2}\]です。ここで\(\delta \equiv \delta_2-\delta_1\)としました。さらにこの転置行列を求めましょう。
\[(A^{-1})^\top = \frac{1}{\sin \delta} \left( \begin{array}{cc} -\sin \delta_2 & -\cos \delta_2 \\ \sin \delta_1 & \cos \delta_1 \end{array} \right) \tag{3}\](1)式に戻り、\(X \equiv E_x / a_1, Y \equiv E_y / a_2\)のようにすると
\[\left( \begin{array}{c} X \\ Y \end{array}\right) = A \left( \begin{array}{c} \cos \tau \\ \sin \tau \end{array}\right) \ \underbrace{\Longrightarrow}_{A^{-1} \times} \ A^{-1} \left( \begin{array}{c} X \\ Y \end{array}\right) = \left( \begin{array}{c} \cos \tau \\ \sin \tau \end{array}\right)\]これの全体を転置させたものは
\[(X, Y) (A^{-1})^\top = (\cos \tau, \sin \tau)\]より、2つの内積を取ると
\[(X, Y) (A^{-1})^\top A \left( \begin{array}{c} X \\ Y \end{array}\right) = (\cos \tau, \sin \tau) \left( \begin{array}{c} \cos \tau \\ \sin \tau \end{array}\right) = \cos^2 \tau + \sin^2 \tau = 1 \tag{4}\]この最左辺に現れた行列部分を計算しましょう。(2), (3)式より
\[\begin{align} (A^{-1})^T A^{-1} &= \frac{1}{\sin^2 \delta} \left( \begin{array}{cc} -\sin \delta_2 & -\cos \delta_2 \\ \sin \delta_1 & \cos \delta_1 \end{array} \right) \left( \begin{array}{cc} -\sin \delta_2 & \sin \delta_1 \\ -\cos \delta_2 & \cos \delta_1 \end{array} \right) = \frac{1}{\sin^2 \delta} \left( \begin{array}{cc} 1 & -\cos \delta \\ -\cos \delta & 1 \end{array} \right) \notag \\ &\equiv \frac{1}{\sin^2 \delta} B \tag{5} \end{align}\]となります。最後の行列部分を\(B\)と定義しました。では、さらにこの行列\(B\)の固有値\(\lambda\)・固有ベクトル\(\mathbf{u}\)を求めましょう。
\[B \mathbf{u} = \lambda \mathbf{u} \ \Longrightarrow \ (B-\lambda I) \mathbf{u} = \mathbf{0}\]\(I\)は2x2の単位行列です。逆行列\((B- \lambda I)^{-1}\)が存在するとき、\(\mathbf{u}=\mathbf{0}\)となり、これは不適です。よって逆行列が存在しない条件として
\[\begin{align} &\mathrm{det} (B-\lambda I) = \left| \begin{array}{cc} 1-\lambda & -\cos \delta \\ -\cos \delta & 1-\lambda \end{array}\right| =(1-\lambda)^2 -\cos^2 \delta = \lambda^2 -2\lambda + \sin^2 \delta = 0 \notag \\ &\Longrightarrow \ \lambda = \frac{2 \pm \sqrt{4 - 4 \sin^2 \delta}}{2} = 1 \pm \cos \delta \notag \end{align}\]\(|\cos \delta| \leq 1\)より、固有値\(\lambda\)は\(\delta\)に関わらず、2つとも正の値をとります。
行列\(B\)の固有値をそれぞれ\(\lambda_1 = 1+\cos \delta, \lambda_2 = 1-\cos \delta\)とおきましょう。また\(\lambda_1, \lambda_2\)に対応する固有ベクトルをそれぞれ\(\mathbf{u}_1 =(a, b), \mathbf{u}_2=(c, d)\)とします。
よって規格化された固有ベクトルは
\[\mathbf{u}_1 = \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ -1 \end{array} \right)\] \[B \mathbf{u}_2 = \left( \begin{array}{cc} 1 & - \cos \delta \\ - \cos \delta & 1 \end{array} \right) \left( \begin{array}{c} c \\ d \end{array} \right) = \left( \begin{array}{c} c - d\cos \delta\\ d- c\cos \delta \end{array} \right) = \lambda_2 {\bf u}_2 = \left( \begin{array}{c} c- c\cos \delta \\ d- d \cos \delta \end{array} \right) \ \Longrightarrow \ c= d\]よって規格化された固有ベクトルは
\[\mathbf{u}_2 = \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ 1 \end{array} \right)\]次に行列\(B\)の対角化を考えます。対角化させるためのユニタリ行列を\(U\)とすると、2つの固有ベクトルより
\[U = \frac{1}{\sqrt{2}}\left( \begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array} \right) \tag{6}\]そして
\[U^{-1} = \frac{1}{\frac{1}{\sqrt{2}} |1\cdot 1 - 1 \cdot (-1)|} \left( \begin{array}{cc} 1 & -1\\ 1 & 1 \end{array} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & -1\\ 1 & 1 \end{array} \right) = U^T \tag{7}\]以上から
\[U^{-1} B U = \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right) \ \Longrightarrow \ B = U \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right) U^{-1} \tag{8}\]のようになります。(8)式を(4)式に代入すると
\[\frac{1}{\sin^2 \delta} (X, Y) U \left( \begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right) U^{-1} \left( \begin{array}{c} X \\ Y \end{array} \right) = 1\]ここで
\[\left( \begin{array}{c} \xi \\ \eta \end{array} \right) = U^{-1} \left( \begin{array}{c} X \\ Y \end{array} \right)\]とおくと
\[(\xi, \eta) = \left( U^{-1} \left( \begin{array}{c} X \\ Y \end{array} \right) \right)^T = (X, Y) (U^{-1})^T \underbrace{=}_{(7)} (X, Y) U\]より
\[(\xi, \eta) \left( \begin{array}{cc} \lambda_1 & 0\\ 0 & \lambda_2 \end{array} \right) \left( \begin{array}{c} \xi \\ \eta \end{array}\right) = \lambda_1 \xi^2 + \lambda_2 \eta^2 = \sin^2 \delta = (1-\cos \delta) (1+\cos \delta)\]ここから\(\delta = 0, 2\pi, 4\pi, \dots\)のときは\(\xi=0\)、\(\delta = \pi, 3\pi, \dots\)のときは\(\eta=0\)となります。よって
\[\left\{ \begin{array}{ll} \xi = 0 & (\delta = 2n\pi) \\ \eta = 0 & (\delta = (2n+1)\pi) \\ \frac{\xi^2}{1-\cos \delta} + \frac{\eta^2}{1+ \cos \delta} = 1 & ({\rm otherwise}) \end{array} \right. \tag{9}\]のようになります。ただし\(n=0, 1, 2, \dots\)です。
楕円偏光
これまでの議論から、\(\delta\)が特定の値とき以外は\(\xi, \eta\)は楕円を描くことがわかります。
この\(X, Y\)および\(\xi, \eta\)を図から理解すると以下のようになります。
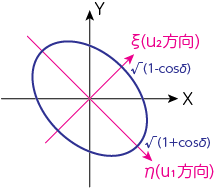
(9)式から、\(\xi, \eta\)平面内では電磁波の状態は一般に楕円で表されることがわかります。\(\xi, \eta\)は\(X, Y\)にそれぞれユニタリ変換を施したものなので、電磁波の状態は\(XY\)平面内でも楕円のままです。
このとき電磁波は楕円偏光であるといいます。
直線偏光と円偏光
以下では電場の\(x, y\)成分の位相差\(\delta\)によって偏光状態がどのように変化するかを見ていきましょう。以下では簡単のため\(a_1 = a_2 = a\)とします。
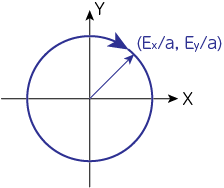
\(\delta = \pi/2\)のとき
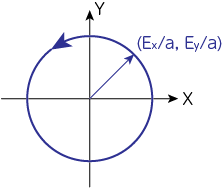
(9)式より\(\xi^2+\eta^2=1\)から、これは真円を描きます。これを円偏光状態と呼びます。ではこの円偏光はどちら回りになるでしょうか。
元々の問題設定から
のように式変形されます。これは下図のように時計回りであることがわかります。これを右回り円偏光と呼びます。
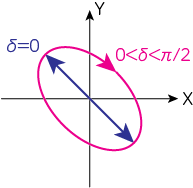
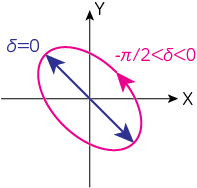
\(\delta=0\)のとき
(9)式より\(\xi = 0\)となり、これは\(\eta\)方向の直線であることがわかります。これを直線偏光と呼びます。
実際の電場成分で考えると、\(0<\delta<\pi/2\)の範囲では、\(\delta\)が減少するにしたがって右回りの楕円偏光になることがわかります。
\(\delta=- \pi/2\)のとき
(9)式より、再び\(\xi^2 + \eta^2=1\)から、これは円偏光になります。実際の電場成分を考えると
\[E_x = a \cos (\tau + \delta_1), \quad E_y = a \sin (\tau + \delta_1)\]より、この電場ベクトルは下図のような反時計回りであることがわかります。これを左回り円偏光と呼びます。
\(\delta\)が\(-\pi/2 < \delta < 0\)のときには、左回りの楕円偏光となります。
右回り・左回りの定義とヘリシティー
円偏光の右回り・左回りは見方に依存した定義で、客観性を欠く表現です。実際、業界によって同じ右回りで全く逆の回り方を指しています。例えば光学業界では、電磁波が進んでくる方向に向かって時計回りを右回りと定義します。これは電磁波を受け取る観測者の立場にたった定義です。観測者が電磁波(光子)と同じ速度(光速度)で動くことはできないため、外から見る人間の立場に立たざるを得ないとも言えるでしょう。一方、プラズマ業界では、波や粒子の進行方向に右ねじが進方向を右回りと定義しています。プラズマで扱う粒子が主に質量を持った粒子かつ観測者によって粒子の進行方向が異なる可能性があるため、このような定義の方が便利ということを反映したものです。
これらの事情から業界によって定義が異なっていますが、場合によっては業界を越えてより客観的な定義を用いた方が便利な場合があります。それが
のように定義されるヘリシティ(helicity)です。ここで\(\mathbf{s}\)は円偏光電磁波のスピンベクトル、\(\mathbf{k}\)は波数ベクトルです。円偏光電磁波のスピンベクトルの向きは、偏光ベクトルの回転方向に右ねじを回転したときにねじが進む方向として定義されます。ヘリシティは正か負かのみ意味があり、電磁波の進行方向とスピンの向きが同じとき(左回り)を正、逆(右回り)を負のヘリシティと定義します。
量子力学の話題
電磁波(光子)のヘリシティや角運動量(スピン)といった話題を学ぶと、量子力学の遷移により放出される光子の数などに言及することができます。光子のスピン角運動量は\(\mp \hbar\)ということが知られています。この知識を踏まえた上で、以下のような中性水素における電子のエネルギー準位の遷移について考えてみましょう。
\[n=2, \ell=0 \ \longrightarrow \ n = 1, \ell=0\]ここで\(n\)はエネルギー準位を表す整数(主量子数、\(n=1\)が基底状態で\(n=2\)が第一励起状態など)、そして\(\ell\)は軌道角運動量を表す自然数(方位量子数、\(\ell=0\)が角運動量0の状態)です。よってこれは角運動量が0の状態から、再び0の状態へと遷移していることがわかります。
\(n=2 \rightarrow 1\)のエネルギー差に相当するエネルギー\(E = h\nu\)を持つ光子を出さなくてはいけません。ここで角運動量\(\hbar\)の光子一個を放出したと考えましょう。すると遷移前後の角運動量の関係は
となり、遷移前後で角運動量が保存していないことがわかります。よって角運動量保存を満たすような遷移にするためには\(-\hbar\)の光子も同時に放出しなければならないことがわかります。
光子を2個出さなければならないことから、この遷移は起こりにくく、これを禁制遷移と呼びます。