Table of contents

2体緩和
参考文献

2体緩和

ここでは、銀河や球状星団のように多数の恒星からなる系の中を運動する1つの天体に着目します。この天体が、系の中の個別の恒星との近接相互作用により運動に対して大きな影響を受けるまでの時間(緩和時間)を大雑把に見積もってみましょう。

2体問題からの洞察

緩和時間とはその名の通り、緩和を受けるまでにかかる時間のことです。重力によって相互作用を及ぼしあう恒星が存在するとき、それらは衝突によって運動エネルギーが交換されることで熱力学的に緩和し、熱平衡に向かって分布関数が進化していきます。もともとの(その系に似つかわしくないような大きな)速度を持つ恒星が系に存在していたとしても、その系の中を運動していく途中で他の恒星から重力相互作用を受け、次第に速度が変化していきます。ある程度の時間が経つと、その恒星はその系に相応しい速度を持って運動するようになり、晴れて系の仲間入りとなるわけです。
ここでは衝突パラメータ\(b\)ですれ違う2つの天体1, 2を考えましょう。この2つの天体はどちらも同じ質量\(m\)を持っているとします。定式化を簡単にするため、天体2の静止系において、天体1が十分遠くから初速度\(v\)で\(x\)方向に飛んでくる場合を考えます。天体1は無限遠から天体2に接近し、再び無限遠に飛び去ると考えると、天体1の軌道は双曲線となります。

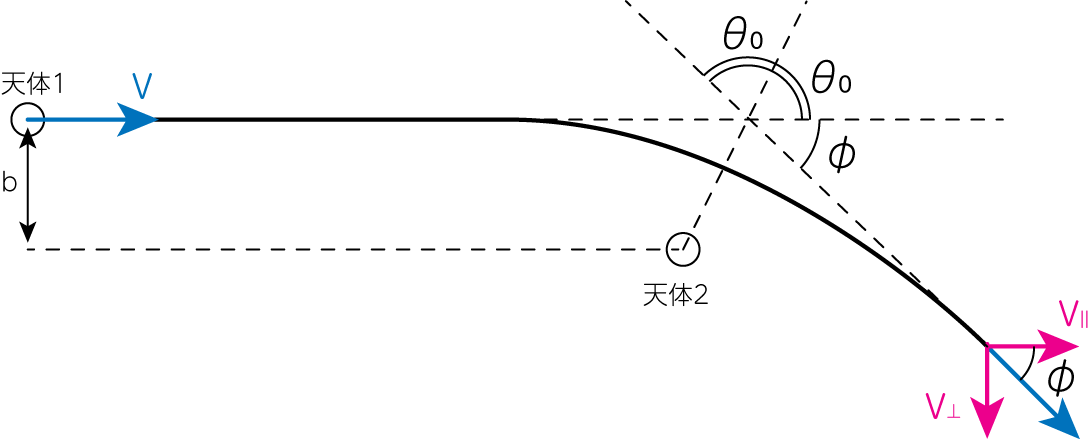
この軌道は2体問題から

\[r = \frac{\frac{h^2}{GM}}{1 + \frac{h^2 B}{GM} \cos (\theta - \theta_0)} \tag{1}\]

となります。ここで\(h\)は角運動量、\(M = m + m\)はこの2体系全体の質量、そして\(B, \theta_0\)はそれぞれ初期条件などから決まる定数です。上図より

\[\phi + 2 \theta_0 = \pi \ \Longrightarrow \ \theta_0 = \frac{\pi - \phi}{2} \tag{2}\]

\(\theta=\pi\)のとき\(r \rightarrow \infty\)より、(1)式の分母が0になることを用いると

\[1 + \frac{h^2 B}{GM} \cos \left( \pi - \frac{\pi - \phi}{2} \right) = 1 + \frac{h^2B}{GM} \cos \left( \frac{\phi}{2} + \frac{\pi}{2}\right) = 1 - \frac{h^2 B}{GM} \sin \frac{\phi}{2} = 0 \ \Longrightarrow \ \sin \frac{\phi}{2} = \frac{GM}{h^2 B} \tag{3}\]

さらに図より

\[v_\perp = v \sin \phi = 2 v \sin \frac{\phi}{2} \cos \frac{\phi}{2} = 2 v \frac{GM}{h^2 B} \sqrt{1-\frac{G^2 M^2}{h^4 B^2}} \tag{4}\]

となります。\(h, B\)が定まっていないため、これを\(v, b\)で表してみましょう。 2体問題において\(h\)は保存量なので、無限遠にいた初期条件から求めます。すると上図より

\[h = \vert \mathbf{r} \times \mathbf{v} \vert = bv \tag{5}\]

です。さらに[2体問題の(20)式]から

\[B = \sqrt{\frac{2E}{h^2} + \frac{G^2 M^2}{h^4}}\]

と求まっているのでした。ここで\(E\)は天体1の全エネルギーです。2体問題においては全エネルギーも保存するため、無限遠にいた初期条件から\(E = v^2 / 2\)となります。よって

\[B = \sqrt{\frac{1}{b^2} + \frac{G^2 M^2}{b^4 v^4}} \tag{6}\]

のようになります。これらを(4)式に代入すると

\[v_\perp = \frac{2v GM}{b^2 v^2} \frac{v^2 b^2}{\sqrt{G^2 M^2 + v^4 b^2}} \frac{v^2 b}{\sqrt{G^2 M^2 + v^4 b^2}} = \frac{2 v^3 b G M}{G^2 M^2 + v^4 b^2} = \frac{2 b v^3}{G M} \frac{1}{1+\frac{v^4 b^2}{G^2 M^2}} \equiv \delta v_\perp \tag{7}\]

のように求まります。初期には垂直方向成分がゼロだったことから、天体2との相互作用により生じた変化分という意味をこめて、最後に\(\delta v_\perp\)と定義しています。また運動量保存則から、天体1だけでなく、天体2にも\(\delta v_\perp\)の速度変化がもたらされます。

多粒子との衝突に拡張と緩和時間

これまでは天体2が静止している座標系において、天体1が無限遠から入射してきた場合を考えてきました。今度はこれを任意の粒子数に拡張させましょう。下図のようにある天体が静止している系において、無限遠から個数密度\(n\)で天体を入射させます。簡単のため、天体の質量は全て\(m\)、また入射してくる天体達の速度も\(v\)で一定であるとします。

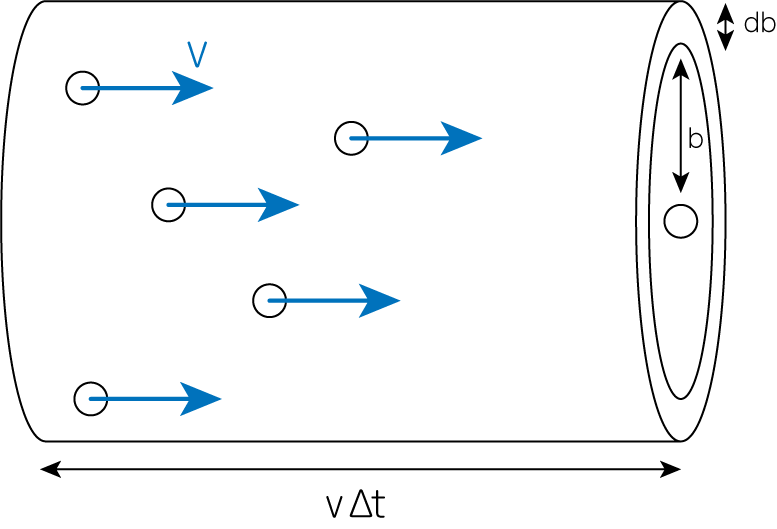
時間間隔\(\Delta t\)の間にインパクトパラメータが\(b \sim b+db\)で入射してくる天体の数は、微小幅\(db\)の円柱の体積より\(2 \pi b \cdot db \cdot v\Delta t \cdot n\)となります。これら一つ一つが(7)式の速度変化を静止している天体にもたらすと考えると、その速度変化の総和\(\vert \delta v_\perp \vert^2\)は

\[\vert \delta v_\perp \vert^2 = 2\pi b db v \Delta t n \frac{4 b^2 v^6}{G^2 M^2} \frac{1}{\left( 1+\frac{v^4 b^2}{G^2 M^2}\right)^2} \tag{8}\]

のようになります。

2乗和を考えたのは、そのままでは様々な方向からの入射によりそれらがキャンセルするためです。2乗和から積算値を考えることで、速度がどの程度のタイムスケールで変化したのかを探ることができます。

分母の\((\cdots)^2\)部分がややこしいため、ここで\(\frac{v^4 b^2}{G^2 M^2} \gg 1\)という近似を用います。これは

\[\frac{v^2}{b} \gg \frac{GM}{b^2} \tag{9}\]

のように変形することができます。左辺は天体からの距離が\(b\)のときに受ける遠心力、右辺は距離\(b\)で受ける重力です。するとこの式は遠心力が重力よりもすごく大きく、双曲線運動で飛び去っていくことに対応しています。もし\(\frac{v^2}{b} \simeq \frac{GM}{b^2}\)であれば、これは遠心力と重力がほぼ釣り合っているような円運動を意味します。

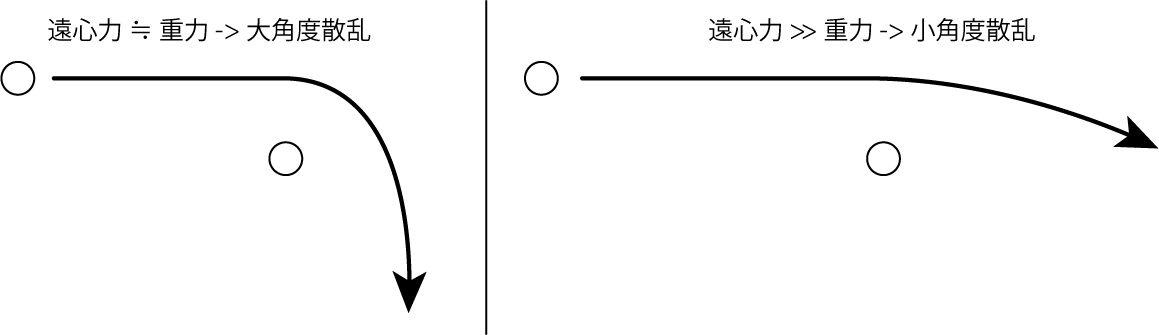
以上の議論から、この問題設定では分母の1を無視する近似が正しいことがわかります。よって

\[\vert \delta v_\perp \vert^2 \simeq \frac{8\pi b^3 db v^7 \Delta t n}{G^2 M^2} \frac{G^4 M^4}{v^8 b^4} = \frac{8\pi n G^2 M^2 \Delta t}{vb} db \tag{10}\]

これを\(b\)について積分すれば、様々な衝突パラメータですれ違う天体から受ける速度変化を合計することができます。積分範囲を\([b_\mathrm{min}, b_\mathrm{max}]\)のように考えると

\[\vert \delta v_\perp \vert^2 = \frac{8\pi n G^2 M^2 \Delta t}{v} \int_{b_\mathrm{min}}^{b_\mathrm{max}} \frac{1}{b} db = \frac{8\pi n G^2 M^2 \Delta t}{v} \ln \left( \frac{b_\mathrm{max}}{b_\mathrm{min}} \right) \tag{11}\]

と計算されます。ここで\(\Lambda \equiv \frac{b_\mathrm{max}}{b_\mathrm{min}}\)と定義し、(11)式に出てきた\(\ln \Lambda\)をCoulomb logarithmと呼びます。この部分は対数の依存性しかないため、そこまで大きな寄与を与えません。しかし(9)式の仮定から\(b_\mathrm{min} \sim \frac{GM}{v^2}\)、そして\(R\)を系のサイズとすると\(b_\mathrm{max} \sim R\)のように考えることができます。よって

\[\ln \Lambda \simeq \ln \left( \frac{R v^2}{GM} \right) \tag{12}\]

のように見積もることができます。
(11)式から\(\vert \delta v_\perp \vert^2 \simeq v^2\)となるまでにかかる時間を求めてみましよう。

\[\Delta t = \frac{v^3}{8\pi n G^2 M^2 \ln \Lambda} \equiv t_\mathrm{relax} \tag{13}\]

の\(t_\mathrm{relax}\)を緩和時間(relaxation time)と呼びます。これは天体が他の多数の天体とすれ違うことで、天体の速度が元の速度\(v\)の大きさと同程度変化するまでにかかる時間を表します。

横断時間との比較

ここで天体が系を横切るのにかかる典型的なタイムスケール(crossing timescale)を考えましょう。これは大雑把に

\[t_\mathrm{cross} \simeq \frac{R}{v} \tag{14}\]

と計算できます。すると(13)式と(14)式の比は

\[\frac{t_\mathrm{relax}}{t_\mathrm{cross}} \simeq \frac{v^4}{8\pi n G^2 M^2 R \ln \Lambda} \tag{15}\]

ここでビリアル定理より、系全体の質量を\(M_0\)とすると

\[v^2 \simeq \frac{G M_0}{R} \tag{16}\]

のように計算されます。これを(15)式に用いると

\[\frac{t_\mathrm{relax}}{t_\mathrm{cross}} \simeq \frac{\frac{M_0^2}{M^2}}{8\pi n R^3 \ln \Lambda} \tag{16}\]

ここで\(M = 2m\)は、2体問題を考えたときの2天体の質量の合計でした。ここではさらに大雑把に系全体の天体数を\(N \simeq M_0 / M\)とします。そして系が球形をしていると考え、数密度を\(n = \frac{N}{\frac{4\pi}{3} R^3}\)と計算すると

\[\frac{t_\mathrm{relax}}{t_\mathrm{cross}} \simeq \frac{N}{6 \ln \Lambda} \underbrace{\simeq}_{(12), (16)} \frac{N}{6 \ln N} \tag{17}\]

を得ます。

途中の近似の仕方や導出過程には様々な手法があり、それらによっては分母の係数6が8になったりします。

(17)式の右辺を\(n_\mathrm{relax}\)と定義すれば、この式は\(t_\mathrm{relax} \simeq n_\mathrm{relax} t_\mathrm{cross}\)と書けます。この式から、\(n_\mathrm{relax}\)は天体の運動が緩和するまでに必要な横断回数を表します。

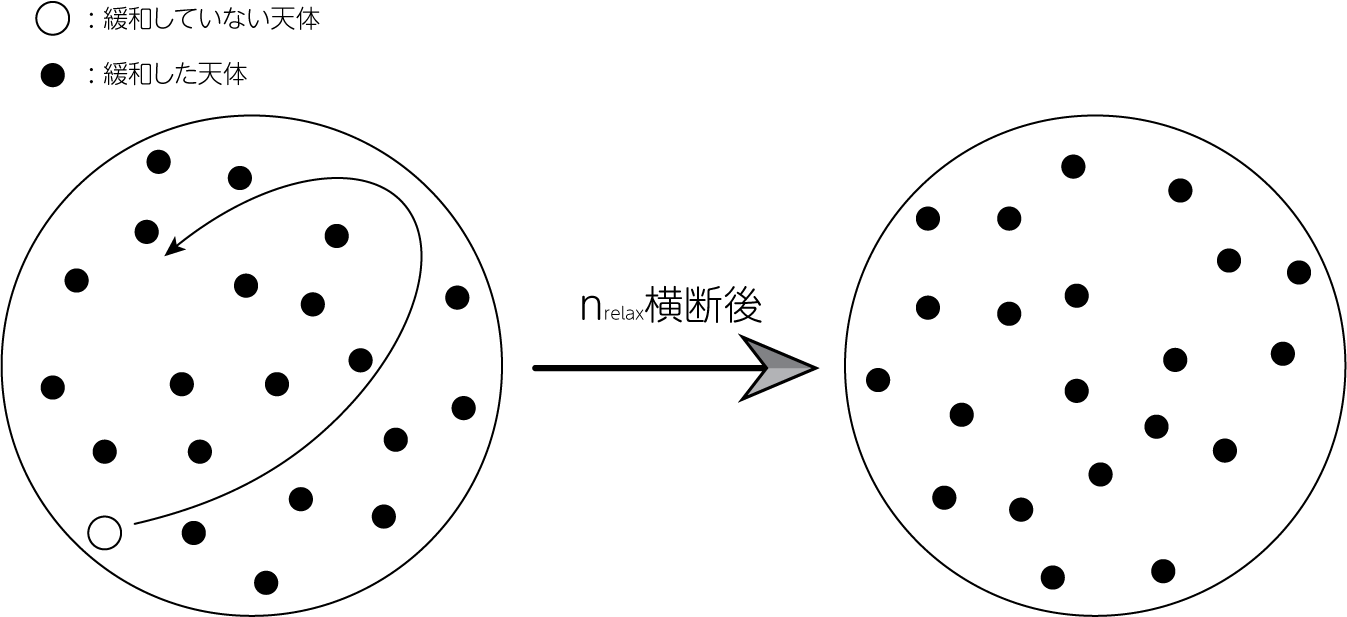
応用: 宇宙に存在する重力多体系は緩和しているか？

(17)式を用いれば、宇宙に存在する星団や銀河などの多体系はすでに緩和して落ちついた状態にあるかどうかを判別することができます。下表は様々な系に対して、それを構成する天体の典型的な速度\(v\)・系の典型的サイズ\(R\)・典型的な天体要素数\(N\)から、\(n_\mathrm{relax}, t_\mathrm{cross}, t_\mathrm{relax}\)を算出したものです。

天体	\(v \ [\mathrm{km/s}]\)	\(R \ [\mathrm{pc}]\)	\(N\)	\(t_\mathrm{cross} \ [\mathrm{yr}]\)	\(n_\mathrm{relax}\)	\(t_\mathrm{relax} \ [\mathrm{yr}]\)
散開星団	\(1\)	\(1\)	\(10^{2-3}\)	\(10^6\)	\(4-24\)	\(10^7\)
球状星団	\(10\)	\(10\)	\(10^6\)	\(10^6\)	\(10^4\)	\(10^{10}\)
銀河中心部	\(10^2\)	\(1\)	\(10^7\)	\(10^4\)	\(10^5\)	\(10^9\)
銀河全体	\(10^2\)	\(10^4\)	\(10^{11}\)	\(10^8\)	\(10^8\)	\(10^{16}\)
銀河団	\(10^3\)	\(10^6\)	\(10^3\)	\(10^9\)	\(24\)	\(10^{10}\)

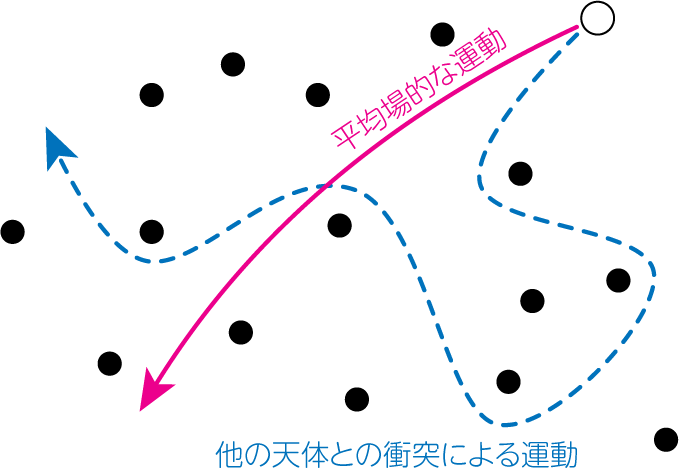
この表の一番右の列に着目しましょう。散開星団は10Myr程度で緩和することがわかりますが、球状星団は10Gyr経過しないと緩和しないことがわかります。宇宙年齢が13.8Gyr程度なので、球状星団が宇宙初期に生まれたならばギリギリ緩和しているかどうかという程度とわかります。ただし、球状星団は中心部と外縁部で恒星密度が大きく異なることなどを考慮すると、実は中心部では緩和が効いていることが知られています。銀河中心部の狭い領域は1Gyr程度で緩和していますが、銀河全体を見渡すと\(t_\mathrm{relax} \gg (宇宙年齢)\)より、緩和しているとは言えません。これは逆に、銀河全体のスケールで見ると、短い時間スケール(例えば\(10 t_\mathrm{cross} \sim 1\)Gyr)では個別の星々との相互作用による緩和過程は重要ではなく、多数の恒星によりできる平均場的な重力ポテンシャルに従った運動をすると言えます。

銀河団も球状星団と同じく、10Gyr程度の緩和時間を持ちます。もし宇宙初期から今まで、銀河団どうしの大きな合体によりメンバー銀河の数が大きく増加するなどの劇的な変化が起こっていなければ、\(z=0\)の近傍に存在する銀河団はギリギリ緩和しているかもしれないと言えます。しかし銀河団はその進化過程で多数の合体を経ているため、実際に緩和しているかどうかはその他の観測結果を組み合わせて決める必要があるでしょう。

参考文献

牧野淳一郎, “重力多体系の数値計算”
小久保英一郎, “重力多体系の物理の基礎”