Table of contents
\(\zeta\)関数
ゼータ関数には色々な種類がありますが、普通は宇宙物理の人間が示しているのはリーマンのゼータ関数のことです。これはやはりオイラーによって導入されていました。しかし、後にゲオルグ・フリードリヒ・ベルンハルト・リーマンが大きな貢献をしたことと、その時に好んで\(\zeta\)(ゼータ)を用いて表現ため、この名前がつきました。
定義
ゼータ関数を、ガンマ関数を用いて
\[\zeta (z) = \frac{1}{\Gamma(z)} \int_0^\infty \frac{u^{z-1}}{e^u-1} du\]と定義します。
\[\begin{aligned} \zeta (z) &= \frac{1}{\Gamma(z)} \int_0^\infty \frac{e^{-u} u^{z-1}}{1-e^{-u}} \underbrace{=}_{無限等比級数} \frac{1}{\Gamma(z)} \int_0^\infty e^{-u} u^{z-1} \sum_{k=0}^\infty e^{-ku} du = \frac{1}{\Gamma(z)} \int_0^\infty u^{z-1} \sum_{k=1}^\infty e^{-ku} du \\ &= \frac{1}{\Gamma(z)} \sum_{k=1}^\infty \int_0^\infty u^{z-1} e^{-ku} du \end{aligned}\]\(v = ku\)とおくと
\[\zeta (z) = \frac{1}{\Gamma(z)} \sum_{k=1}^\infty \int_0^\infty (v/k)^{z-1} e^{-v} \frac{dv}{k} = \frac{1}{\Gamma(z)} \sum_{k=1}^\infty \frac{1}{k^z} \underbrace{\int_0^\infty v^{z-1} e^{-v} dv}_{=\Gamma(z)} = \sum_{k=1}^\infty \frac{1}{k^z}\]となります。ガンマ関数で表現されていたゼータ関数が、整数の逆数の無限和で表現されることがわかりました。
では実際のガンマ関数の値はどのようなものになるでしょうか。\(\zeta(1), \zeta(2), \zeta(4)\)の値を具体的に求めてみましょう。
\(\zeta (1)\)の計算
関数\(f(x) = 1/x (x>0)\)を考えてみましょう。ある正の整数\(k\)に対して
\[\int_k^{k+1} \frac{1}{x} dx \lt \int_{k}^{k+1} \frac{1}{k} dx = \frac{1}{k} [x]_k^{k+1} = \frac{1}{k}\]であることがわかります(下図参照)。
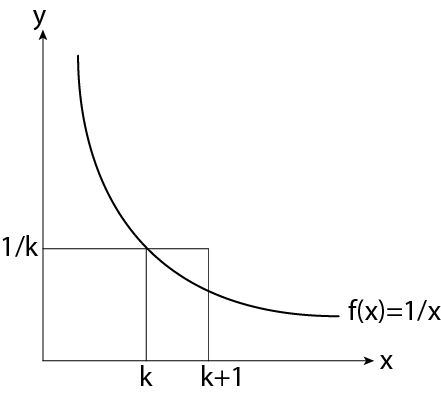
\(\sum_{k=1}^n\)で和をとると、最左辺は
\[\int_1^{n+1} \frac{1}{x} dx = [\ln x]_1^{n+1} = \ln (n+1)\] \[\therefore \ln (n+1) \lt \sum_{k=1}^n \frac{1}{k}\]この両辺を\(\lim_{n\rightarrow \infty}\)とすると\(\zeta(1) = \infty\)であることがわかります。
\(\zeta (2)\)の計算
唐突ですが\(y=x^2 (-\pi \leq x \leq \pi)\)が繰り返されている周期関数\(f(x)\)をフーリエ級数で表現することを考えましょう。
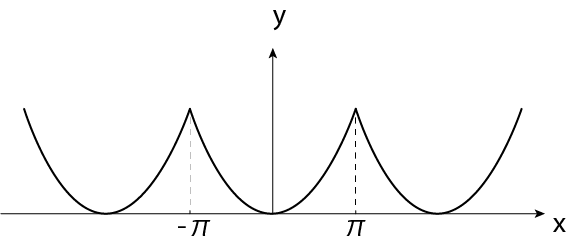
以上より
\[f(x) = \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4}{n^2} (-1)^n \cos nx\]フーリエ級数の公式より係数\(a_0\)は\(1/2\)したものを足していることに注意しましょう。ここに\(x=\pi\)を代入すると
\[\pi^2 = \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4}{n^2}(-1)^{2n} = \frac{\pi^2}{3} + 4\zeta(2) \ \Longrightarrow \ \therefore \ \zeta(2) = \frac{\pi^2}{6}\]これはバーゼルの問題と呼ばれており、他にも解法が存在します。ご自身で探求されるのも良いでしょう。
\(\zeta (4)\)の計算
同様に\(y=x^4 (-\pi \leq x \leq \pi)\)が繰り返されている周期関数\(f(x)\)をフーリエ級数で表現することを考えましょう。
\[a_0 = \frac{1}{\pi} \int_{-\pi}^\pi x^4 dx = \frac{1}{5\pi} [x^5]^\pi_{-\pi} = \frac{2\pi^4}{5}\] \[\begin{aligned} a_n &= \frac{1}{\pi} \int_{-\pi}^\pi x^4 \cos nx dx = \frac{1}{\pi} \left[ \frac{1}{n} x^4 \sin n x \right]_{-\pi}^\pi - \frac{4}{n\pi} \int_{-\pi}^\pi x^3 \sin nx dx \\ &= \frac{4}{n\pi} \left[ \frac{1}{n} x^3 \cos nx \right]_{-\pi}^\pi - \frac{12}{n^2} \underbrace{\frac{1}{\pi}\int_{-\pi}^\pi x^2 \cos nx dx}_{\zeta(2)での計算より} = \frac{8\pi^2}{n^2} (-1)^n - \frac{48}{n^4} (-1)^n \end{aligned}\] \[b_n = \frac{1}{2\pi} \int_{-\pi}^\pi x^4 \sin nx dx \underbrace{=}_{奇関数} 0\]以上より
\[f(x) = \frac{\pi^4}{5} + \sum_{n=1}^\infty \left( \frac{8\pi^2}{n^2} -\frac{48}{n^4} \right) (-1)^n \cos nx\]ここに\(x=\pi\)を代入すると
\[\pi^4 = \frac{\pi^4}{5} + \sum_{n=1}^\infty \left( \frac{8\pi^2}{n^2} -\frac{48}{n^4} \right) (-1)^{2n} = \frac{\pi^4}{5} + 8\pi^2 \zeta(2) - 48 \zeta(4) \ \Longrightarrow \ \therefore \ \zeta(4) = \frac{\pi^4}{90}\]参考文献
- 数理系のための基礎と応用 微分積分II -理論を中心に-, 金子
- 解析入門I, 杉浦
- 物理数学, 高橋
- 物理数学I, 福山, 小形
- 2017 大学入試短期集中ゼミ数学 III, 福島 國光
- 高校数学の美しい物語
- Wolfram MathWorld