チェビシェフ多項式

多項式の導出

突然ですが、以下の積分について考えましょう。

\[\frac{1}{\pi} \int_0^\pi \cos m \theta \cos n \theta d\theta \qquad (m, n \in \mathbb{Z})\]

これは\(m, n\)によってその積分値が変わるので、場合分けが必要です。まずは\(m \neq n\)の場合について計算しましょう。

\[\frac{1}{\pi} \int_0^\pi \cos m \theta \cos n \theta d \theta = \frac{1}{\pi} \int_0^\pi \frac{\cos (m+n) \theta + \cos (m-n) \theta}{2} d\theta = \frac{1}{2\pi} \left[ \frac{\sin (m+n) \theta}{m+n} - \frac{\sin (m-n) \theta}{m-n}\right]_0^\pi = 0\]

次に\(m = n\)のときです。

\[\frac{1}{\pi} \int_0^\pi \cos^2 m \theta d\theta = \frac{1}{\pi} \int_0^\pi \frac{\cos 2m\theta + 1}{2} d\theta = \frac{1}{2\pi} \left[ \frac{\sin 2m\theta}{2m} + \theta\right]_0^\pi = \frac{1}{2}\]

同様に\(n=-m\)のときも

\[\frac{1}{\pi} \int_0^\pi \cos m \theta \underbrace{\cos (-m) \theta}_{=\cos m\theta} d\theta = \frac{1}{2}\]

と計算できます。最後に\(m=n=0\)の場合、すなわちコサインが常に1の場合には、この積分値は1となります。以上から

\[\frac{1}{\pi} \int_0^\pi \cos m \theta \cos n \theta d\theta = \frac{\delta_{mn} + \delta_{m, -n}}{2} \tag{1}\]

ここで\(x = \cos \theta \ (d\theta = -dx/ \sqrt{1-x^2})\)のように変数変換を行いましょう。さらに

\[T_m (x) \equiv \cos m \theta = \cos ( m \cos^{-1} x) \tag{2}\]

を定義しておくと、(1)式は

\[\int_{-1}^1 \frac{T_m(x) T_n(x)}{\sqrt{1-x^2}} dx = \left\{ \begin{array}{cc} 0 & (m \neq n) \\ \pi / 2 & (m = n > 0) \\ \pi & (m=n=0) \end{array} \right. \tag{3}\]

\(T_{-m}(x) = T_m (x)\)の偶関数性から、(3)式では\(m, n \geq 0\)のみを考えることにしています。(2)式で定義される\(T_m(x)\)を\(m\)次のチェビシェフ多項式と呼びます。また(3)式より関数列\(\{T_m(x)\}\)は\(\sqrt{1-x^2}\)を重みとする直交関数の組であるとわかります。

漸化式と微分方程式

それではこの多項式が満たす漸化式を証明しておきましょう。そこで以下の計算を行います。

\[\begin{aligned} e^{i(n+1)\theta} + e^{i(n-1)\theta} &= \cos (n+1) \theta + i \sin (n+1) \theta + \cos (n-1) \theta + i \sin (n-1) \theta \\ &= \cos n \theta \cos \theta - \sin n \theta \sin \theta + \cos n \theta \cos \theta + \sin n \theta \sin \theta \\ & \qquad \qquad + i (\sin n \theta \cos \theta + \sin \theta \cos n \theta + \sin n \theta \cos \theta - \sin \theta \cos n \theta)\\ &= 2 \cos n \theta \cos \theta + 2i \sin n\theta \cos \theta \end{aligned}\]

\(x = \cos \theta\)であることに注意しながら、この両辺の実部のみを比較すると

\[T_{n+1} (x) + T_{n-1} (\theta) = 2x T_n(x) \tag{4}\]

という漸化式を得ます。
チェビシェフ多項式が満たす微分方程式について証明しましょう。\(T_n (x) = \cos n \theta\)より、この多項式は\(\frac{d^2 y}{d\theta^2} + n^2 y = 0\)の解であることを心に留めておくと

\[\frac{d}{d\theta} = \frac{dx}{d\theta} \frac{d}{dx} = -\sin \theta \frac{d}{dx}\] \[\frac{d^2}{d\theta^2} = \frac{dx}{d\theta} \frac{d}{dx} \left( \frac{dx}{d\theta} \frac{d}{dx} \right) = - \sin \theta \frac{d}{dx} \left( - \sin \theta \frac{d}{dx}\right) = \sin^2 \theta \frac{d^2}{dx^2} + \sin \theta \left( \frac{d}{dx} \sin \theta \right) \underbrace{=}_{\sin \theta = \sqrt{1-x^2}} (1-x^2) \frac{d^2}{dx^2} - x \frac{d}{dx}\]

より

\[(1-x^2) T_n'' - x T_n' + n^2 T_n = 0 \tag{5}\]

となります。\((1-x^2) y'' - xy' + n^2 y=0\)をチェビシェフの微分方程式と呼びます。さらに\(\frac{d}{dx} = - \frac{1}{\sin \theta} \frac{d}{d\theta}\)より

\[(1-x^2) T_n' = n \sin \theta \sin n\theta = - \frac{n}{2} \{ \cos (n+1) \theta - \cos (n-1) \theta \} = -\frac{n}{2} (T_{n+1} - T_{n-1})\]

です。ここに(4)式を用いると

\[(1-x^2) T_n' = -nx T_n + n T_{n-1} \tag{6}\]

という微分漸化式を満たすことを証明することもできました。

具体的な形とその性質

チェビシェフ多項式の具体的な関数形は以下のように表されます。

\[T_0(x) = 1, \quad T_1(x) = x, \quad T_2(x) = 2x^2-1, \quad T_3 (x) = 4x^3 -x, \quad T_4(x) = 8x^4-8 x^2+1\]

以下にいくつかの\(n\)に対するチェビシェフ多項式を図示するPythonスクリプトを示します。

#!/usr/bin/env python3 

import numpy as np
import matplotlib.pyplot as plt
import scipy.special as sc

if __name__ == '__main__':
    # set variables
    ix = 100
    xmin = -1.0
    xmax = 1.0
    nmin = 0
    nmax = 6
    # set x coordinate
    x = np.linspace(xmin, xmax, ix)
    # main loop of plotting Chebyshev polynomials
    for n in range(nmin, nmax):
        ei = sc.eval_chebyt(n, x)
        string = "n={}".format(n)
        plt.plot(x, ei, label=string)
        plt.legend()
    # make plot window
    plt.show()

このスクリプトによって図示された結果h以下のようになります。

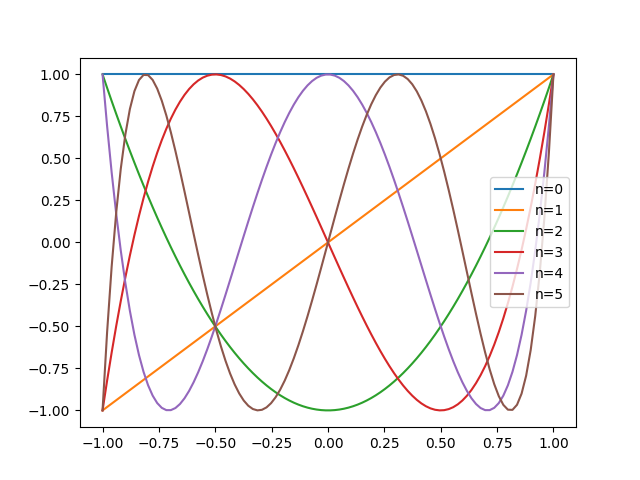
グラフからわかるように、チェビシェフ多項式はその定義域\([-1, 1]\)において\(\\| T_n (x) \\| \leq 1\)を満たします。またこの区間において、比較的均一に分布している様子も見て取れます。このため、ある区間で与えられた関数\(f(x)\)を有限のn次までの\(\{ T_n (x)\}\)を用いて多項式展開で近似を行うと、その結果は他の直交多項式を用いて得られたものよりも小さな誤差で済むことが知られています。より詳しくは、\(\{T_n(x)\}\)のn次までにより関数\(f(x)\)を展開近似した\(F_n(x)\)に対して誤差\(\\| f(x)-F(x)\\|\)の最大値\(\max \\| f(x) - F_n(x)\\|\)が最小となります。このことから、チェビシェフ多項式により展開近似を行ったものが最良の矜持となり、これをチェビシェフ多項式のミニマックス性と呼びます。このような性質のために、チェビシェフ多項式は数値解析において非常に重要な多項式です。

参考文献

[1] 田島, 近藤, “改訂演習工科の数学4, 複素関数”
[2] 中山, “裳華房フィジックスライブリー, 物理数学II”
[3] 福山, 小形, “基礎物理学シリーズ3, 物理数学I”
[4] 伊理正夫, 藤野和建, “数値計算の常識”