地平線
ここでは粒子的地平線(particle horizon)と事象の地平線(event horizon)について記述します。Robertson-Walker計量における固有距離より、光子が\(dt\)秒間に進む固有距離は
\[d\chi = \frac{c dt}{a(t)}\]これを積分したものに\(a(t)\)をかければ、実際に光子が進んだ距離となります。
\[\ell = a \int_{t_1}^{t_2} \frac{c dt}{a(t)} \tag{1}\]粒子的地平線
これは宇宙が始まってから現在までに光子が到達できる最大の距離を表します。よって\(t_1 = 0\)(宇宙の始まり)、\(t_2 = t\)(現在の時刻)のようにしたものを
\[\ell_p = a \int_0^t \frac{c dt}{a} \tag{2}\]粒子的地平線のイメージを掴むために、簡単のため\(a(t) = a_0 t^n\)のような形で考えましょう。関数形から\(n>1\)のとき加速度膨張、\(n<1\)のとき減速膨張と考えられます。
事象の地平線
これは現在の時刻\(t\)から無限大の時間をかけて光が到達することができる距離を表します。よって\(t_1 = t, t_2 = \infty\)のようにしたものを(1)式に代入した
\[\ell_\mathrm{ev} = a \int_t^\infty \frac{c dt}{a} \tag{3}\]が事象の地平線です。
イメージを掴む
以下では簡単のために、宇宙膨張が\(a(t) = a_0 t^n\)のように書かれるとします。このとき
\[\dot{a} = n a_0 t^{n-1} \ \Longrightarrow \ \ddot{a} = n (n-1) a_0 t^{n-2}\]から、\(n>1\)では\(\ddot{a} > 0\)で加速度膨張、\(n<1\)では\(\ddot{a}<0\)で減速膨張に対応することがわかります。
減速膨張宇宙
減速膨張宇宙\((n<1)\)のとき
\[\ell_p = c t^n \int_0^t t^{-n} dt = c t^n \left[ \frac{t^{1-n}}{1-n}\right]_0^t = \frac{c t}{1-n}\] \[\ell_\mathrm{ev} = c t^n \int_t^\infty t^{-n} dt = c t^n \left[ \frac{t^{1-n}}{1-n}\right]_t^\infty = \infty\]粒子的地平線が時間とともに増加していくのは、減速膨張宇宙だからという一言に尽きます。時間とともに宇宙膨張が緩やかになることで、時間をかければ遠方からの光も届くようになるためです。
では減速膨張の場合になぜ事象の地平線が無限大に発散するのか、それは以下のように時空図を用いて理解することができます。
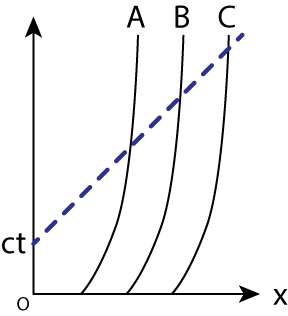
Minkowski座標の時空図中において、最初ある位置に静止していた減速運動をする粒子A, B, Cの世界線を描きます。次に\(x=0\)である時刻\(t\)に静止している観測者からの光円錐を青点線で描きます。すると時間が経過するに従って、粒子A, B, Cの世界線は光円錐内部に入って行くことがわかります。このことから、減速膨張宇宙では無限の時間をかければ情報のやり取りが可能であること、すなわち事象の地平線が無限大になることがわかります。
加速度膨張の場合
加速度膨張宇宙\((n>1)\)のとき
\[\ell_p = c t^n \int_0^t t^{-n} dt = c t^n \left[ \frac{t^{1-n}}{1-n}\right]_0^t = \infty\] \[\ell_\mathrm{ev} = c t^n \int_t^\infty t^{-n} dt = c t^n \left[ \frac{t^{1-n}}{1-n}\right]_t^\infty = \frac{ct}{n-1}\]加速度膨張のときになぜ事象の地平線が有限の値となるのか、これも先程と同様に時空図を用いて理解してみましょう。
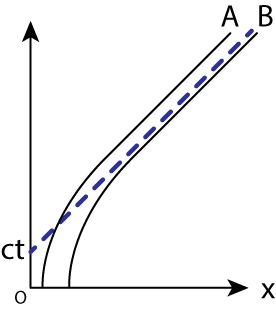
今度は加速度運動をする粒子の世界線を描きます。時刻\(t\)に原点\(x=0\)に静止している観測者が情報のやり取りをできる範囲を光円錐を用いて明確にすると、加速度運動をする粒子も光速度に近づくため、これ以上は交わることなく漸近するような粒子がいることがわかります(例えば粒子Bとは無限の時間をかけても交わることがありません)。よって無限の時間をかけても、有限の広さの範囲しか情報のやり取りをすることができないことを示しています。
よりわかりやすく共動座標で考えると、加速度膨張のときの事象の地平線は
のように時間とともに減少していきます。先程の図で、時間の経過とともに(観測者が\(ct\)軸上を上に動いていくと)遠方の点Bが最初に見えなくなったのち、次に点Aが見えなくなるということから分かる通り、遠方から順に見えなくなっていくことがわかります。
アインシュタイン・ド・ジッター宇宙の場合
このとき\(a(t) = a_0 e^{H t}\)のように書けるので
\[\ell_p = e^{H t} \int_0^t \frac{c dt}{e^{H t}} = \frac{c}{H} (e^{H t} -1)\]のように時間とともに指数関数的に増加します。事象の地平線は以下のようになります。
\[\ell_\mathrm{ev} = e^{H t} \int_t^\infty \frac{cdt}{e^{H t}} = \frac{c}{H}\]です。事象の地平線はハッブル長で一定となります。これは2点間の距離が宇宙の指数関数膨張により引き伸ばされ、この半径を超えるとお互いに情報交換をすることができなくなることを示しています。