自転の効果と恒星風の影響

自転の効果

恒星の自転のように、光子の平均自由行程よりも長い距離スケールの運動は、発光粒子と吸収粒子との間に速度差をもたらしません。よって吸収量、すなわち吸収線の等価幅には影響を及ぼしませんが、吸収線の形を変化させることが知られています。
恒星は自転しているため、表面の各点は私たちに対してそれぞれ異なる視線速度を持ちます。そのため、私たちが観測する吸収線は、それぞれの視線速度に対応するドップラーシフトを受けた吸収線の重ね合わせとなります。

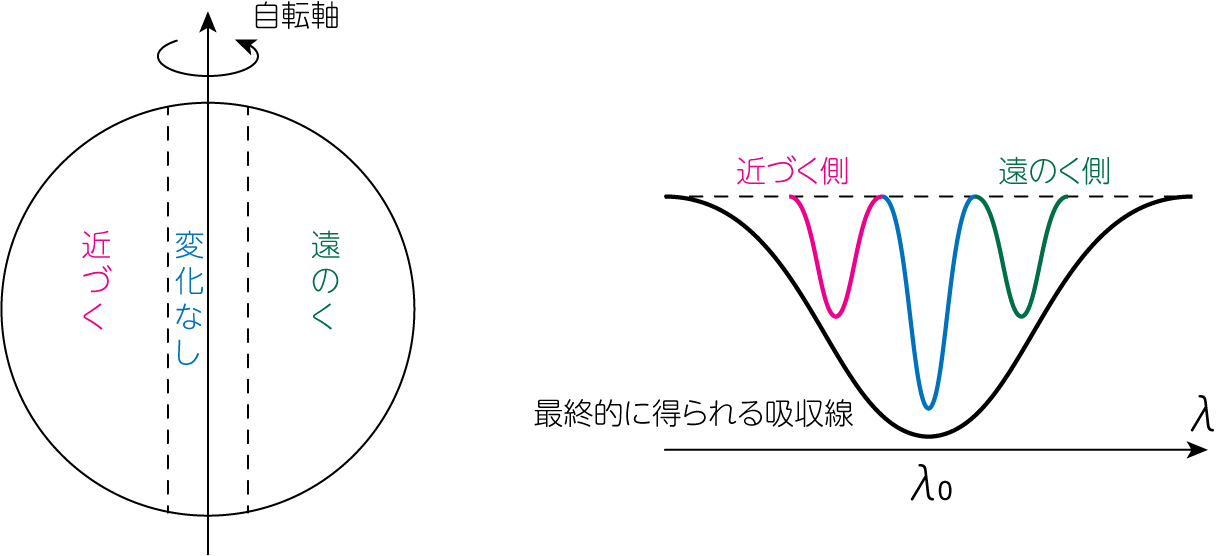
下左図のように、自転軸を\(\theta =0\)の方向とし、私たちの方向を\(\varphi = 0\)とする球座標で考えましょう。

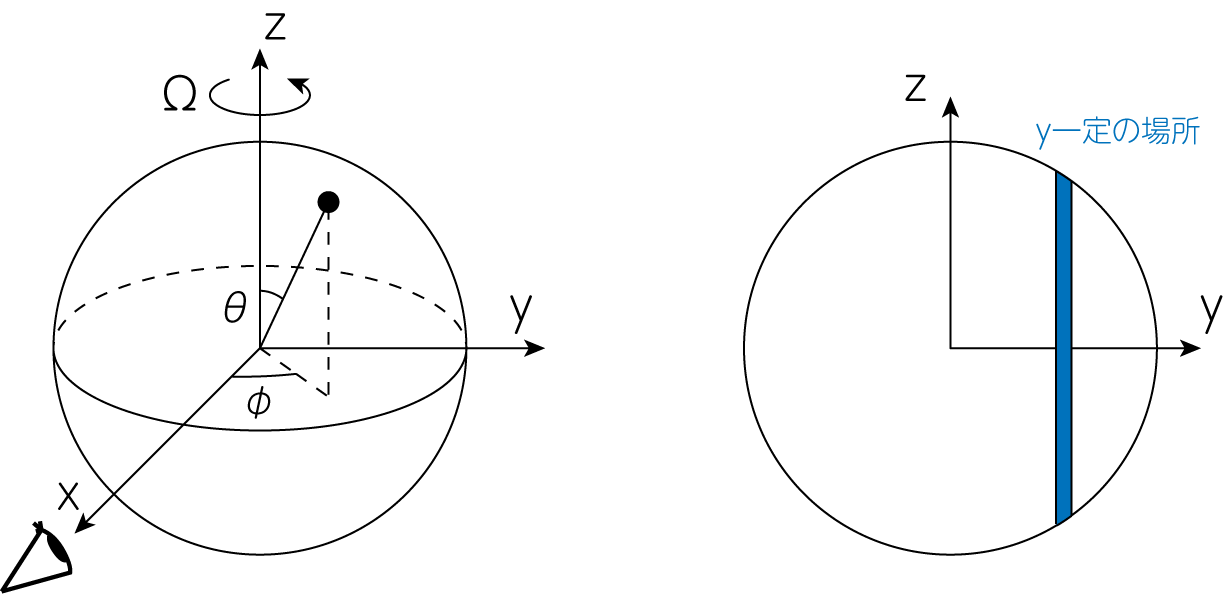
自転角速度を\(\Omega\)、恒星の半径を\(R\)とすると、\((\theta, \varphi)\)で表される恒星表面の各点での自転速度は\(\Omega R \sin \theta\)です。また視線方向は\(\theta = \pi/2\)の位置であるとすると、視線速度は\(\Omega R \sin \theta \sin \varphi\)のようになります。自転軸を\(z\)軸、私たちの方向を\(x\)軸とする直交座標系において、\(y = R \sin \theta \sin \varphi\)より、恒星表面で\(y\)が一定の部分が視線速度一定の領域となります。すなわち、恒星表面を平面に投影したとき、自転軸に平行な直線上で視線速度が一定となります(上右図参照)。
ここまでの議論では、自転軸と視線方向が垂直であると仮定しました。しかし、一般に自転軸と視線方向のなす角度を\(i\)と書くと、視線速度は

\[v_\mathrm{rad} = \Omega R \sin \theta \sin \varphi \sin i = v_\mathrm{eq} y \sin i\]

のように表されます。ここで\(v_\mathrm{eq} \equiv \Omega R\)は、恒星の赤道での自転速度を表します。さらに\(y\)は恒星の半径\(R\)で規格化されているとします。
自転を無視した場合、恒星表面のどこから出てくる光に対しても、ある吸収線の輪郭は同じで\(\phi (\lambda - \lambda_0)\)で表されるとします。このとき、観測される吸収線内でのresidual fluxは

\[\frac{F_\lambda}{F_c} = \frac{\int_{2\pi} \phi(\lambda - \lambda_0) I_c(\theta) \cos \theta d\omega}{\int_{2\pi} I_c (\theta) \cos \theta d\omega} = \phi(\lambda - \lambda_0)\]

のようになります。ここで\(\theta\)は、\(x\)軸方向(視線方向)となす角度で、\(R^2 \cos \theta d\omega\)は恒星表面を平面に投影したときの面積要素を表します。
自転がある場合、恒星表面の各点が私たちに対して視線速度\(v_\mathrm{rad}(y)\)で動いているので、各点での吸収線の中心波長は

\[\lambda_0 + \frac{v_\mathrm{eq} y \sin i}{c} = \lambda_0 + y \Delta \lambda_L \qquad \left( \Delta \lambda_L \equiv \frac{v_\mathrm{eq} \sin i}{c}\right)\]

のようにシフトします。このとき、観測される吸収線内でのフラックスは

\[F_\lambda = \int_{2\pi} \phi (\lambda - \lambda_0 - y \Delta \lambda_L) I_c (\theta) \cos \theta d\omega\]

のように表されます。さらに\(I_c (\theta)\)は、周縁減光パラメータを\(\epsilon\)と書いて

\[I_c (\theta) = I_c (0) \{ 1-\epsilon (1- \cos \theta) \}\]

のように書くことができます。 \(\theta=\pi/2\)、すなわち恒星の赤道では\(I_c (\theta) = I_c (0) (1-\epsilon)\)となることからわかるように、\(0<\epsilon<1\)は周縁減光の強さを表すものです。 \(\epsilon \rightarrow 0\)は周縁減光の影響を考えない極限を表し、\(\epsilon \rightarrow 1\)では強く周縁減光の影響を受けている極限を表します。
ここで、実際の観測に合わせるために、球座標\((\theta, \varphi)\)から、投影面上での直交座標\((y, z)\) (恒星の半径\(R\)で規格化された座標)に変換しましょう。 \(\cos \theta = \sqrt{1-\sin^2 \theta} = \sqrt{1-y^2-z^2}\)の様に表し、さらに球面での積分を投影面での積分\(\cos \theta d\omega = dz dy\)に変換すると

\[\begin{aligned} F_\lambda &= 2 I_c (0) \int_{-1}^1 dy \phi (\lambda - \lambda_0 - y \Delta \lambda_L) \int_0^\sqrt{1-y^2} dz \left( 1-\epsilon + \epsilon \sqrt{1-y^2-z^2} \right) \\ &= I_c (0) \int_{-1}^1 dy \phi (\lambda - \lambda_0 - y \Delta \lambda_L) \left\{ 2(1-\epsilon) \sqrt{1-y^2} + \frac{\pi}{2} \epsilon (1-y^2) \right\} \end{aligned}\]

のように計算されます。一方、連続フラックスは

\[F_c = 2\pi I_c(0) \int_0^{\pi/2} (1-\epsilon + \epsilon \cos \theta) \cos \theta \sin \theta d\theta = \pi I_c (0) \left( 1-\frac{\epsilon}{3}\right)\]

のようになります。したがって、吸収線内のresidual fluxは

\[\frac{F_\lambda}{F_c} = \int_{-1}^1 dy \phi (\lambda-\lambda_0 -y \Delta \lambda_L) G(y) \qquad \left( G(y) \equiv \frac{2(1-\epsilon) \sqrt{1-y^2} + \frac{\pi}{2} \epsilon (1-y^2)}{\pi \left( 1-\frac{\epsilon}{3}\right)}\right)\]

と表されます。 \(G(y)\)は、恒星表面の各点での吸収線を、その場所の視線速度によるドップラーシフトだけ波長をずらして積分することを表しています。 \(\Delta \lambda_L\)に比べて吸収線本来の幅が非常に狭い場合、\(\phi (\lambda - \lambda_0 - y \Delta \lambda_L)\)をデルタ関数で近似すると

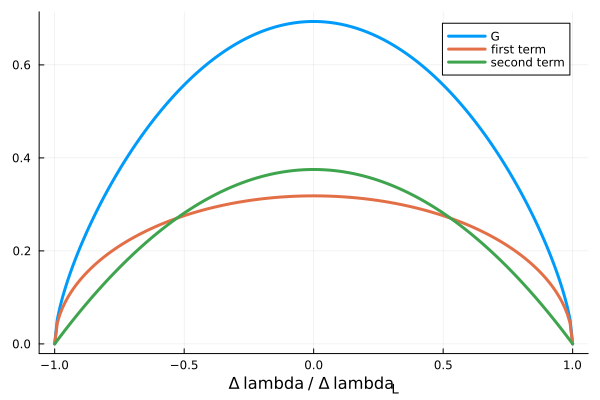
\[\frac{F_\lambda}{F_c} \simeq G(\Delta \lambda / \Delta \lambda_L)\]

となります。ここで\(\Delta \lambda \equiv \lambda - \lambda_0\)です。 \(G(\Delta \lambda / \Delta \lambda_L)\)の形を下図に示します。青線は\(G\)、橙線は第一項、そして緑線は第二項を表します。またこの図は\(\epsilon = 0.6\)として作図を行いました。周縁減光により、視線速度が大きい部分の寄与が小さくなっていることがわかります。

高速自転星のスペクトル線は自転によって広がりますが、このときの吸収線内の各波長は星表面の投影面の\(y\)座標に対応します。すなわち、太陽以外の恒星は点光源としてしか観測されませんが、高速自転星の場合には表面をある程度分解して見ることができると言えるでしょう。大きな黒点や星の振動により表面に温度や速度のむらができている場合、吸収線の輪郭に凸凹が形成され、それが時間とともに移動していく現象が観測されます。この吸収線輪郭の変動から恒星表面の模様を再構築する方法を、ドップラーイメージングと呼びます。

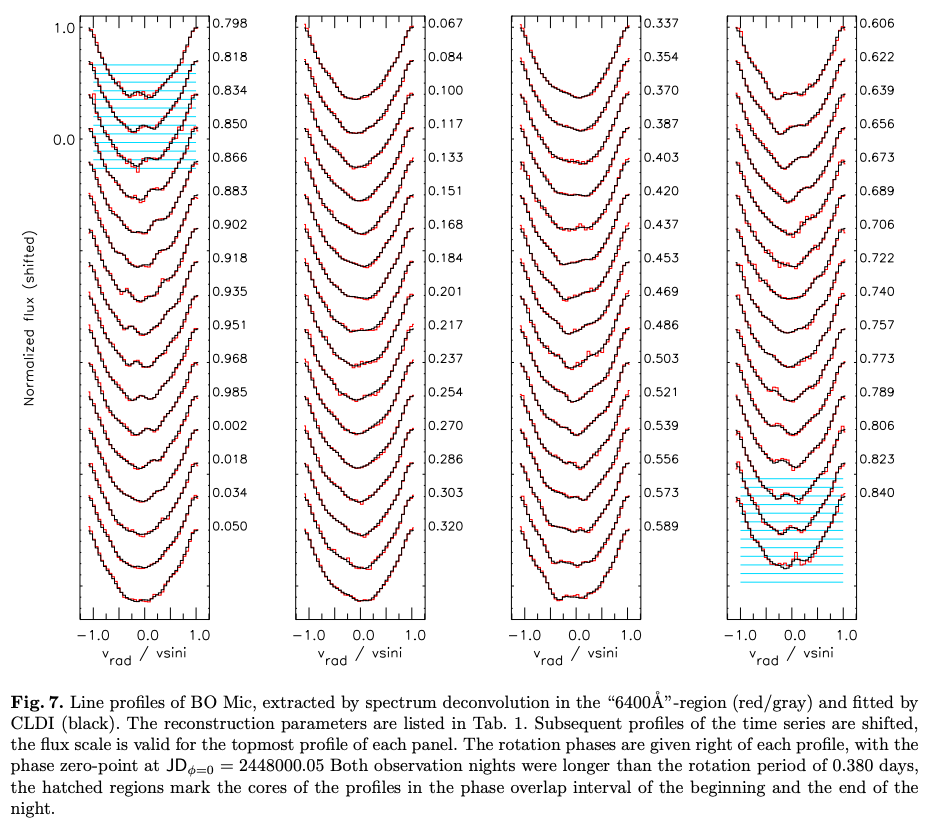
上図はWolter et al., 2005の観測で得られた、若いK型褐色矮星の吸収線の時間変化の様子です。上から下に時間が経過するにつれて、吸収線に存在する凸凹が左から右に移動している様子が伺えます。この凸凹は、恒星表面に存在する黒点(starspots)に起因しており、高速の自転により恒星表面を移動していくためと考えられています。

恒星風の影響: P-Cygni profile

恒星風が強い恒星のスペクトル線には、P-Cygni profileと呼ばれる、吸収成分と輝線成分が組み合わさったものが観測されます。これは吸収線がドップラーシフトにより短波長側に出現することからできる形態です。

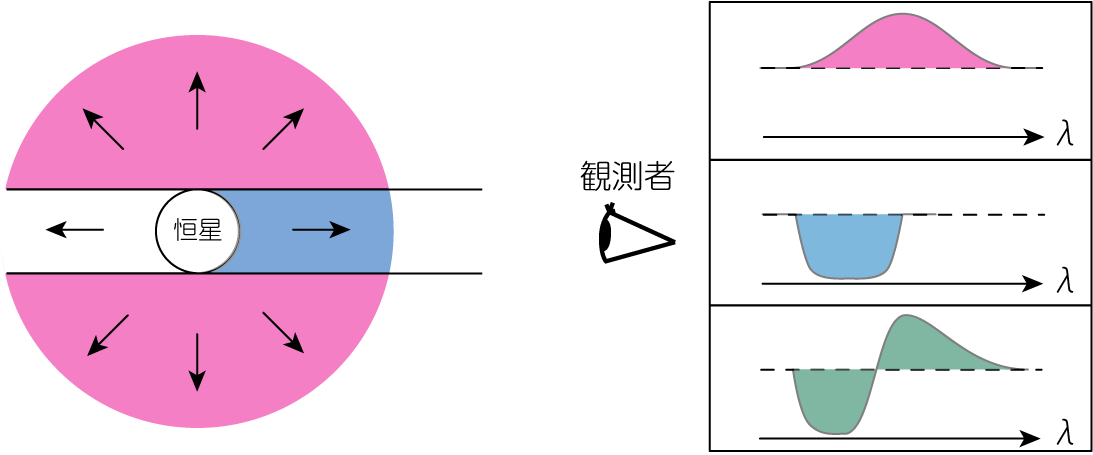
上図左パネルのように、恒星風を右側から見ている状況を考えましょう。するとマゼンダ色部分は輝線を作り、青色部分は恒星を背景にするため吸収線を作ります。また青色部分は観測者に近づくように運動をしているため、短波長側にドップラーシフトした吸収線となります。この2つを重ね合わせると、上図右パネルの緑色で描かれたような、吸収線と輝線からなる特徴的なスペクトルが形成されます。

最近の研究: ブラックホールのアウトフロー

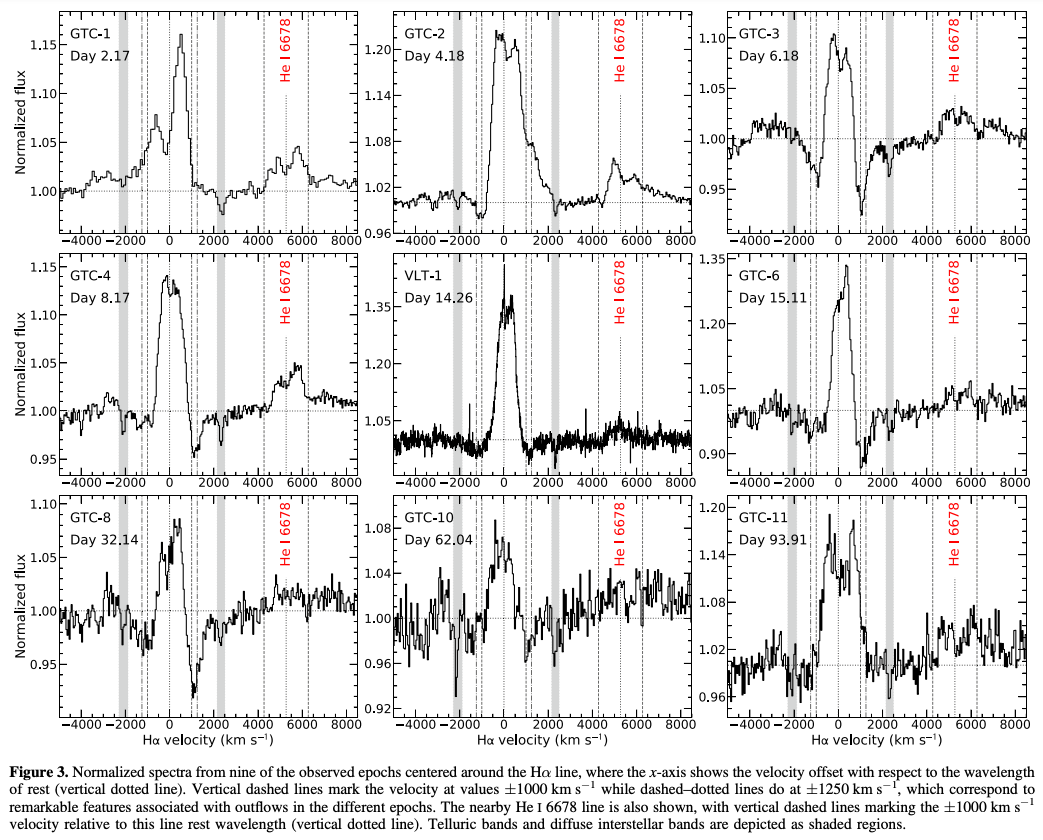
恒星風のようなアウトフローを出しているのは、何も恒星に限った話ではありません。 Sánchez et al., 2022では、ブラックホール候補天体からのアウトバーストを観測しました。このとき観測されたスペクトルには、P-Cygni profileが検出されており、その終端速度はおよそ\(1250 \mathrm{km \ s^{-1}}\)であると結論づけました。この特徴は、ブラックホール降着円盤がハード状態のときに発生したアウトバーストによるものと考えられています。

参考文献

[1] Wolter et al., 2005, “Doppler imaging of Speedy Mic using the VLT, Fast spot evolution on a young K-dwarf star”
[2] Sánchez et al., 2022, “Hard-state Optical Wind during the Discovery Outburst of the Black Hole X-Ray Dipper MAXI J1803-298”
[3] 野本憲一, 定金晃三, 佐藤勝彦, “シリーズ現代の天文学, 恒星”