Table of contents
2体問題
相対座標による表現

まずは万有引力により2つの物体が相互作用しあう系を考えましょう。2つの物体の質量をそれぞれ\(m_a, m_b\)、物体の位置をそれぞれ\(\mathbf{r}_a, \mathbf{r}_b\)とします。すると物体\(a\)に働く重力は
\[\mathbf{F}_a = m \ddot{\mathbf{r}}_a = - G \frac{m_a m_b}{r^2} \frac{\mathbf{r}}{r} \tag{1}\]のように書けます。ここで
\[\mathbf{r} = \mathbf{r}_a - \mathbf{r}_b \tag{2}\]は2つの物体の相対的な位置ベクトルです。以降では2つの物体の重心系を原点とした座標系で考えましょう。すなわち
\[\mathbf{r}_G = \frac{m_a \mathbf{r}_a + m_b \mathbf{r}_b}{m_a + m_b} = \mathbf{0} \ \Longrightarrow \ \mathbf{r}_b = - \frac{m_a}{m_b} \mathbf{r}_a \tag{3}\](2), (3)式より
\[\mathbf{r} = \frac{m_a + m_b}{m_b} \mathbf{r}_a \tag{4}\]これと(1)式より
\[\ddot{\mathbf{r}}_a = - \frac{G (m_a + m_b)}{r^3} \mathbf{r}_a = - \frac{GM}{r^3} \mathbf{r}_a \quad (M \equiv m_a + m_b) \tag{5}\]と書けます。同様に物体\(m_b\)に加わる重力は
\[\ddot{\mathbf{r}}_b = - \frac{GM}{r^3} \mathbf{r}_b \tag{6}\]のように書かれます。(5), (6)式より
\[\ddot{\mathbf{r}}_a - \ddot{\mathbf{r}}_b = - \frac{GM}{r^3} (\mathbf{r}_a - \mathbf{r}_b) \ \underbrace{\Longrightarrow}_{(2)} \ \ddot{\mathbf{r}} = - \frac{GM}{r^3} \mathbf{r} \tag{7}\]となります。
極座標での表現
これまで「\(\mathbf{r}\)は相対座標である」と言うだけで、その形は\((x, y, z)\)のようなデカルト座標であると言うようなことは言ってきませんでした。ここでは\((r, \theta)\)の2次元極座標で考えていきましょう。
\[\dot{\mathbf{r}} = \frac{d}{dt} (r \mathbf{e}_r) = \dot{r} \mathbf{e}_r + r \dot{\theta} \mathbf{e}_\theta \tag{8}\]ここで\(\mathbf{e}_r, \mathbf{e}_\theta\)はそれぞれ\(r, theta\)方向の単位ベクトルです。
\[\ddot{\mathbf{r}} = \ddot{r} \mathbf{e}_r + \dot{r} \dot{\theta} \mathbf{e}_\theta + \dot{r} \dot{\theta} \mathbf{e}_\theta + r \ddot{\theta} \mathbf{e}_\theta + r \dot{\theta} (-\dot{\theta} \mathbf{e}_r) = (\ddot{r} - r \dot{\theta}^2) \mathbf{e}_r + (2\dot{r} \dot{\theta} + r \ddot{\theta}) \mathbf{e}_\theta \tag{9}\]これらより(7)式を\(r, \theta\)方向にそれぞれ分解すると、\(\mathbf{r} = r \mathbf{e}_r\)より
\[\ddot{r} - r\dot{\theta}^2 = - \frac{GM}{r^2} \tag{10}\] \[2 \dot{r} \dot{\theta} + r \ddot{\theta} = 0 \tag{11}\]となります。(11)式の両辺に\(r\)をかけて整理しましょう。
\[2 r \dot{r} \dot{\theta} + r^2 \ddot{\theta} = 0 \ \Longrightarrow \ \frac{d}{dt} (r^2 \dot{\theta}) = 0\]ここから
\[r^2 \dot{\theta} = (一定) = h \tag{12}\]2体問題では\(h\)が保存していることがわかります。特に、単位質量あたりの角運動量である\(h\)をspecific angular momentと呼びます。(12)式を用いると、(10)式は
\[\ddot{r} - \frac{h^2}{r^3} + \frac{GM}{r^2} = 0 \tag{13}\]のように書き直すことができます。(13)式の第二項は遠心力です。
変数変換
ここで\(y = 1/r\)のように変数変換をしましょう。すると時間微分は
\[\frac{d}{dt} = \frac{d}{d\theta} \frac{d\theta}{dt} = \frac{d}{d\theta} \underbrace{\dot{\theta}}_{(12)} = \frac{h}{r^2} \frac{d}{d\theta} = hy^2 \frac{d}{d\theta} \tag{14}\]のように計算されます。よって
\[\frac{dr}{dt} = hy^2 \frac{d}{d\theta} \left( \frac{1}{y}\right) = -h \frac{dy}{d\theta}\]から
\[\frac{d^2 r}{dt^2} = -h \underbrace{\frac{d}{dt}}_{(14)} \frac{dy}{d\theta} = - h^2 y^2 \frac{d^2 y}{d\theta^2}\]となるため、(13)式は
\[- h^2 y^2 \frac{d^2 y}{d\theta^2} - h^2 y^3 + GM y^2 = 0 \ \Longrightarrow \ \frac{d^2 y}{d\theta^2} + y = \frac{GM}{h^2} \tag{15}\]のようになります。この方程式の一般解は特解\(GM/ h^2\)を用いて
\[y = B \cos (\theta - \theta_0) + \frac{GM}{h^2} \tag{16}\]のように書かれます。ここで\(B, \theta_0\)は積分定数です。
楕円軌道
\[r = \frac{1}{B \cos (\theta - \theta_0) + \frac{GM}{h^2}} = \frac{\frac{h^2}{GM}}{1 + \frac{h^2 B}{GM} \cos \theta}\]途中、\(\theta_0 = 0\)としました。以上より
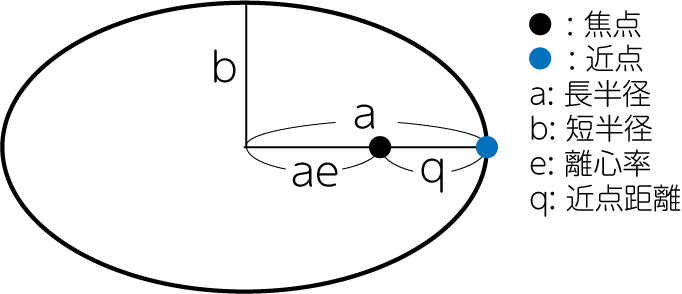
\[r = \frac{a (1-e^2)}{1+e \cos \theta} \quad (a (1-e)^2 = \frac{h^2}{GM}, e = \frac{h^2 B}{GM})\tag{17}\]のように書けば、これは長半径\(a\)と離心率\(e\)の楕円軌道となることがわかります。
積分定数\(B\)を求めるために、(16)式を\(\theta\)で微分しましょう。
\[\frac{dy}{d\theta} = - B \sin (\theta - \theta_0)\]これより
\[B^2 = \left( y - \frac{GM}{h^2}\right)^2 + \left( \frac{dy}{d\theta} \right)^2\]のように計算されます。これを\(r, t\)に戻すと
\[B^2 = \left( \frac{1}{r} - \frac{GM}{h^2}\right)^2 + \frac{\dot{r}^2}{h^2} = \frac{1}{r^2} - \frac{2GM}{h^2 r} + \frac{G^2 M^2}{h^4} + \frac{\dot{r}^2}{h^2} \tag{18}\]ここで全エネルギー
\[E = \frac{1}{2} (v_r^2 + v_\theta^2) - \frac{GM}{r} \underbrace{=}_{(12)} \frac{1}{2} \left( \dot{r}^2 + \frac{h^2}{r^2} \right) - \frac{GM}{r} \tag{19}\]を導入すると、(18)式は
\[B^2 = \frac{2E}{h^2} + \frac{G^2 M^2}{h^4} \tag{20}\]のように書き換えることができます。(20)式より\(E, h\)が決定されれば\(B\)が決定され、(17)式から\(a, e\)が求まることがわかります。
軌道長半径を求める
しかし、実際には\(a\)はこれとは独立に\(E\)から求めることが可能です。\(E\)を評価するために、近点(peri-center)で考えてみましょう。近点距離を\(q\)とすると、近点は\(\dot{r} = 0, r = q\)より
\[E = \frac{h^2}{2q^2} - \frac{GM}{q}\]このとき楕円の幾何学公式から
\[q = a - ae \underbrace{=}_{(17)} \frac{h^2}{GM(1+e)}\]とわかるので、最終的に
\[E = \frac{G^2 M^2 (e^2-1)}{2h^2} = - \frac{GM}{2a} \tag{21}\]と求まります。近点での天体の運動速度から\(E\)が求まれば、(21)式を用いて\(a\)を求めることができます。
ケプラーの第二法則の導出
ケプラーの第二法則は「惑星と太陽とを結ぶ千文が単位時間に描く面積は一定である」と言う、面積速度一定の法則と呼ばれるものです。これを示してみましょう。 下図より、単位時間あたりに線分が描く面積\(\frac{dS}{dt}\)は
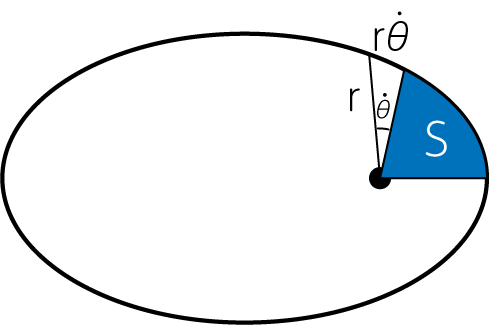
となります。
ケプラーの第三法則の導出
ケプラーの第三法則は「惑星の公転周期を\(P\)としたとき、\(P^2\)が\(a^3\)に比例する」というものです。これを示しましょう。(22)式より
\[S = \frac{1}{2} ht + S_0\]です。1周期の間に惑星と恒星を結ぶ線分が描く面積は、楕円の面積\(\pi a b\)に等しくなります(\(b=\sqrt{1-e^2} a\)は軌道短半径。)よって
\[S - S_0 = \frac{1}{2} h P = \pi ab \ \Longrightarrow \ P = \frac{2}{h} \pi a b = \frac{2\pi}{h} a^2 \sqrt{1-e^2} \underbrace{=}_{(18)} \frac{2\pi a^{3/2}}{\sqrt{GM}} \tag{23}\]となり、ケプラーの第三法則が示されました。
応用: 連星の観測
ここまでの知識を、実際の宇宙物理観測に応用してみましょう。 以下では長期間にわたる位置観測から実際にお互いの周囲を公転運動している様子が確認できている実視連星(visual binary)と、分光から連星であることがわかっている分光連星(spectroscopic binary)について見てみましょう。
実視連星
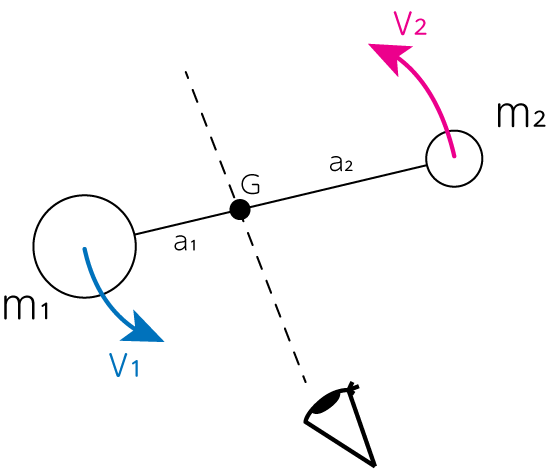
実施連星の場合には、連星(の重心)までの距離さえわかれば、そこから軌道長半径\(a\)を計算することができます。 軌道周期\(P\)は長期にわたる観測からわかっているとすれば、(23)式を用いることで連星の総質量\(M\)が求まります。 さらに重心の定義より
\[a_1 : a_2 = m_2 : m_1\]であることを用いれば、連星系を構成する2つの天体の質量\(m_1, m_2\)を求めることができます。
分光連星
分光連星の場合には、ドップラー効果によりズレた輝線・吸収線の波長を観測することで、それぞれの質量を求めることが可能です。連星系を恒星する2つの天体からの輝線の波長のズレをそれぞれ\(\Delta \lambda_1, \Delta \lambda_2\)とし、ドップラー効果によりズレる前の元の輝線波長を\(\lambda_0\)とすると、波長のズレと2つの連星の視線方向速度\(v_1, v_2\)との間にはそれぞれ
\[\frac{\Delta \lambda_1}{\lambda_0} = \frac{v_1}{c}, \quad \frac{\Delta \lambda_2}{\lambda_0} = \frac{v_2}{c} \ \Longrightarrow \ \frac{\Delta \lambda_1}{\Delta \lambda_2} = \frac{v_1}{v_2} \ \Longrightarrow \ v_1 : v_2 = m_2 : m_1\]の関係が成り立ちます。ここで\(c\)は光速度です。

これとは別に、輝線の波長のズレを長時間モニタリングすることで、\(P\)を求めることができます。さらに速度\(v_1\)を一周期に渡って観測すれば、軌道長半径\(a\)が求まります。これらから(23)式を用いれば連星の総質量\(m_1 + m_2\)が求まり、先程の輝線のズレから求まった質量比と合わせることで、それぞれの質量を決定することができます。
先程の軌道長半径を求める部分では、実はもう少し複雑なことを考えます。気になる方は視線速度法などで調べてみると良いでしょう。
参考文献
野本憲一, 定金晃三, 佐藤勝彦, “恒星”