Table of contents
磁気流体での斜め衝撃波
基礎方程式
磁気流体が2次元運動をしており、そこで衝撃波が発生した場合を考えます。下図のように衝撃波面に垂直な方向を\(x\), 衝撃波面に平行な方向を\(y\)にとります。衝撃波面は\(x\)方向に伝播していきますが、ここではすでに衝撃波の伝播速度と同じ速度で運動する系で衝撃波を見ているものとします。そして\(y\)方向に適当に運動する系に移動することで、衝撃波面の上流側では\(\mathbf{v}_1 \parallel \mathbf{B}_1\)のようになっているものとします。
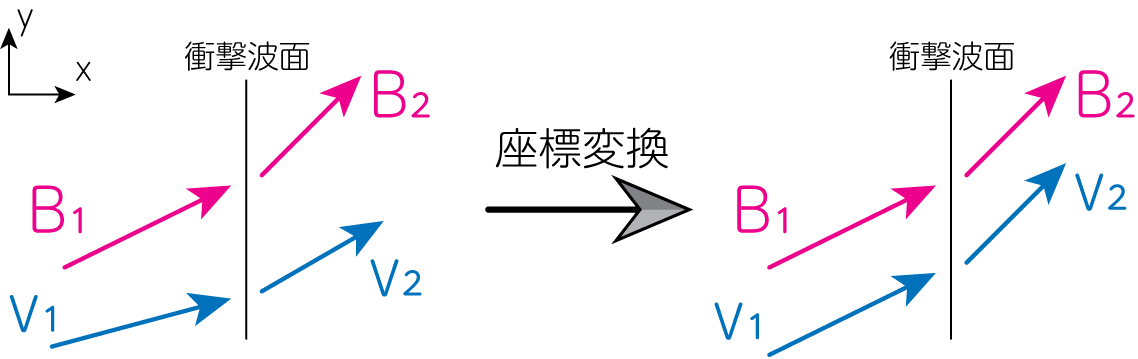
流体の速度は非相対論的で、流体の運動にのみガリレイ変換が施されたと考えます。
また衝撃波は定常状態にあり、等速度で伝播していくとします。以降、衝撃波面の上流側の物理量には1, 下流側の物理量には2の添字をつけて式変形を行います。
磁気流体での垂直衝撃波と同様に、衝撃波面を挟んで成り立つ質量保存則より
続いて運動量保存則です。\(x\)方向の運動量保存は
\[\underbrace{\frac{\partial}{\partial}(\rho v_{x})}_{定常より0} + \partial_j \left\{ \rho v_x v_j - \frac{1}{4\pi} B_x B_j + \left( P + \frac{1}{8\pi} \right) \delta_{xj} \right\} = 0\]から
\[\rho_1 v_{1x} v_{1x} - \frac{1}{4\pi} B_{1x} B_{1x} + P_1 + \frac{1}{8\pi} B_1^2 = \rho_2 v_{2x} v_{2x} - \frac{1}{4\pi} B_{2x} B_{2x} + P_2 + \frac{1}{8\pi} B_2^2 \tag{2}\]垂直衝撃波のときと違い、\(y\)方向の運動量保存も考慮しなければなりません。
\[\rho_1 v_{1y} v_{1x} - \frac{1}{4\pi} B_{1y} B_{1x} = \rho_2 v_{2y} v_{2x} - \frac{1}{4\pi} B_{2y} B_{2x} \tag{3}\]エネルギー保存則より
\[\left( \frac{1}{2} \rho_1 v_1^2 + \rho_1 e_1 + P_1 \right) v_{1x} + S_{1x} = \left( \frac{1}{2} \rho_2 v_2^2 + \rho_2 e_2 + P_2 \right) v_{2x} + S_{2x} \tag{4}\]ここで
\[e = \frac{1}{\gamma - 1} \frac{P}{\rho}, \qquad \mathbf{S} = \frac{c}{4\pi} \mathbf{E} \times \mathbf{B} \tag{5}\]はそれぞれ流体の内部エネルギーとポインティングベクトルです。 オームの法則より、理想磁気流体を考えて電気伝導度が\(\sigma \rightarrow \infty\)とすると
\[\mathbf{j} = \sigma \left( \mathbf{E} + \mathbf{v} \times \frac{\mathbf{B}}{c} \right) \ \Longrightarrow \ \mathbf{E} = \frac{\mathbf{j}}{\sigma} - \mathbf{v} \times \frac{\mathbf{B}}{c} \underbrace{=}_{\sigma \gg 1} - \mathbf{v} \times \frac{\mathbf{B}}{c} \tag{6}\]以上の(4), (5), (6)式より
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma -1} P_1\right) v_{1x} - \frac{1}{4\pi} [(\mathbf{v}_1 \times \mathbf{B}_1) \times \mathbf{B}_1]_x = \left( \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma -1} P_2\right) v_{2x} - \frac{1}{4\pi} [(\mathbf{v}_2 \times \mathbf{B}_2) \times \mathbf{B}_2]_x\]ベクトル解析より
\[\begin{aligned} [(\mathbf{v} \times \mathbf{B}) \times \mathbf{B}]_i &= \epsilon_{ijk} (\mathbf{v} \times \mathbf{B})_j B_k = \epsilon_{ijk} \epsilon_{k \ell m} v_\ell B_m B_k = \epsilon_{kij} \epsilon_{k \ell m} v_\ell B_m B_k \\ &= (\delta_{k\ell} \delta_{im} - \delta_{i\ell} \delta_{km}) v_\ell B_m B_k = v_k B_i B_k - v_i B_k B_k = [(\mathbf{v} \cdot \mathbf{B}) \mathbf{B} - B^2 \mathbf{v}]_i \end{aligned}\]から
\[\begin{align} &\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1\right) v_{1x} - \frac{1}{4\pi} (v_{1x} B_{1x} + v_{1y} B_{1y}) B_{1x} + \frac{1}{4\pi} B_1^2 v_{1x} \notag \\ &= \left( \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma-1} P_2\right) v_{2x} - \frac{1}{4\pi} (v_{2x} B_{2x} + v_{2y} B_{2y}) B_{2x} + \frac{1}{4\pi} B_2^2 v_{2x} \tag{7} \end{align}\]となります。
次に、磁場のガウス則(磁気単極子がないことを表す式)より
が満たされる必要があります。
そして誘導方程式より
磁気流体垂直衝撃波のときと同様に、衝撃波面に垂直に交差するような一辺\(\ell\)の正方形で面積積分すると
\[\begin{align} & \iint_S \nabla \times (\mathbf{v} \times \mathbf{B}) \cdot d\mathbf{S} = \oint_C (\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{s} = (v_{1x} B_{1y}- v_{1y} B_{1x}) \ell - (v_{2x} B_{2y} - v_{2y} B_{2x}) \ell = 0 \notag \\ & \Longrightarrow \ v_{1x} B_{1y}- v_{1y} B_{1x} = v_{2x} B_{2y} - v_{2y} B_{2x} \tag{9} \end{align}\]先程の\(\mathbf{v}_1 \parallel \mathbf{B}_1\)となるような座標系で衝撃波を観測していることから
\[v_{1y} = \frac{B_{1y}}{B_{1x}} v_{1x} \tag{10}\]が成立します。(9), (10)式から、実は衝撃波の下流側でも
\[v_{2y} = \frac{B_{2y}}{B_{2x}} v_{2x} \tag{11}\]すなわち\(\mathbf{v}_2 \parallel \mathbf{B}_2\)が成り立ちます。
式変形
(1)式より
\[\frac{\rho_2}{\rho_1} = \frac{v_{1x}}{v_{2x}} \equiv X \tag{12}\]さらに
\[\frac{P_2}{P_1} \equiv Y, \qquad \frac{B_{2y}}{B_{1y}} \equiv Z \tag{13}\]を定義します。(8), (10), (11)より
\[\frac{v_{2y}}{v_{1y}} = \frac{\frac{B_{2y}}{B_{2x}} v_{2x}}{\frac{B_{1y}}{B_{1x}} v_{1x}} = \frac{B_{2y}}{B_{1y}} \frac{v_{2x}}{v_{1x}} = \frac{Z}{X} \tag{14}\]です。これらを用いて基礎方程式を計算していきましょう。(2), (8), (12), (13), (14)式より式より
\[\begin{aligned} &\rho_1 v_{1x}^2 + P_1 + \frac{1}{8\pi} B_{1y}^2 = \rho_1 v_{1x}^2 \frac{1}{X} + P_1 Y + \frac{1}{8\pi} B_{1y}^2 Z^2 \\ &\Longrightarrow \ \rho_1 v_{1x}^2 \left(1-\frac{1}{X} \right) + P_1(1-Y) + \frac{1}{8\pi} B_{1y}^2 (1-Z^2) = 0 \end{aligned}\]両辺に\(X / \rho_1\)をかけて音速\(C_s^2 = \gamma P / \rho\)を用いて整理すると
\[v_{1x}^2 (X-1) + \frac{C_{s1}^2}{\gamma} X (1-Y) + \frac{1}{8\pi \rho_1} B_{1y}^2 X(1-Z^2) = 0 \tag{15}\]続いて(3), (8), (10), (12), (13), (14)式より
\[\rho_{1} v_{1y} v_{1x} - \frac{1}{4\pi} B_{1y} B_{1x} = \rho_1 v_{1y} v_{1x} \frac{Z}{X} - \frac{1}{4\pi} B_{1y} B_{1x} Z\]これを整理すると
\[Z = \frac{\rho_1 v_{1y} v_{1x} - \frac{1}{4\pi} B_{1y} B_{1x}}{\rho_1 v_{1y} v_{1x} \frac{1}{X} - \frac{1}{4\pi} B_{1y} B_{1x}} \underbrace{=}_{(10)} \frac{v_{1y} v_{1x} - \frac{1}{4\pi \rho_1} \frac{v_{1y}}{v_{1x}} B_{1x}^2}{v_{1y} v_{1x} \frac{1}{X} - \frac{1}{4\pi \rho_1} \frac{v_{1y}}{v_{1x}} B_{1x}^2} = \frac{v_{1x}^2 - \frac{1}{4\pi \rho_1} B_{1x}^2}{v_{1x}^2 - \frac{1}{4\pi \rho_1} B_{1x}^2 X} X\]となります。今、流体の速度ベクトルと磁場ベクトルが平行な系で考えているので、これは
\[Z = \frac{B_{2y}}{B_{1y}} = \frac{v_1^2 - \frac{1}{4\pi \rho_1} B_1^2}{v_1^2 - \frac{1}{4\pi \rho_1} B_1^2 X} X = \frac{v_1^2 - v_A^2}{v_1^2 - v_A^2 X} X \tag{16}\]と変形することができます。ここでアルヴェーン速度を用いました。(14), (16)式より
\[\frac{v_{2y}}{v_{1y}} = \frac{v_1^2 - v_A^2}{v_1^2 - v_A^2 X} \tag{17}\]最後に(7)式の変形を行います。実は
\[- \frac{1}{4\pi} (v_{1x} B_{1x} + v_{1y} B_{1y}) B_{1x} + \frac{1}{4\pi} B_1^2 v_{1x} = \frac{1}{4\pi} B_{1y}^2 v_{1x} - \frac{1}{4\pi} v_{1y} B_{1y} B_{1x} \underbrace{=}_{10} 0\]となります。これは\(\mathbf{v} \parallel \mathbf{B}\)の座標系に移っていることから、\(\mathbf{j} = \mathbf{v} \times \mathbf{B}/c = \mathbf{0}\)に必ずなるためです。よって(7)式は
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1}P_1 \right) v_{1x} = \left( \frac{1}{2} \rho_1 v_2^2 X + \frac{\gamma}{\gamma-1}P_1 Y\right) \frac{1}{X} v_{1x} \ \Longrightarrow \ \frac{1}{2} \rho_1 (v_1^2 - v_2^2) X = \frac{\gamma}{\gamma-1} P_1(Y-X)\]となります。先程と同様に音速\(C_{s}^2 = \gamma P/\rho\)を用いて整理すると
\[Y = X + \frac{\gamma-1}{2 C_{s1}^2} v_1^2 \left( 1-\frac{v_2^2}{v_1^2}\right) X\]となります。ここで\(\mathbf{v} = v_1 (\cos \theta, \sin \theta)\)のように書けることを用いると
\[v_{2x}^2 = \frac{v_{2x}^2}{v_{1x}^2} v_{1x}^2 \underbrace{=}_{(12)} v_1^2 \cos^2 \theta \frac{1}{X^2}, \quad v_{2y}^2 = \frac{v_{2y}^2}{v_{1y}^2} v_{1y}^2 \underbrace{=}_{(14)} v_1^2 \sin^2 \theta \frac{Z^2}{X^2} \tag{18}\]より
\[\begin{aligned} Y &= X + \frac{\gamma-1}{2 C_{s1}^2} v_1^2 \left\{ 1 - \left( \cos^2 \theta \frac{1}{X^2} + \sin^2 \theta \frac{Z^2}{X^2} \right) \right\} X = X + \frac{\gamma-1}{2} \frac{v_1^2}{C_{s1}^2} \frac{X^2 - \cos^2 \theta - Z^2 \sin^2 \theta}{X} \\ &= X + \frac{\gamma-1}{2} \frac{v_1^2}{C_{s1}^2} \frac{X^2 - 1 + \sin^2 \theta (1-Z^2)}{X} \end{aligned}\]以上から
\[1-Y = \frac{2 C_{s1}^2 X(1-X) - v_1^2 (\gamma-1) \{ X^2 - 1+\sin^2 \theta (1-Z^2)\}}{2 C_{s1}^2 X} \tag{19}\]となります。(15), (19)式より
\[v_1^2 \cos^2 \theta (X-1) + \frac{1}{2} X v_{A1}^2 \sin^2 \theta (1-Z^2) + \frac{1}{2\gamma} [2 C_{s1}^2 X(1-X) - v_1^2 (\gamma-1) \{ X^2 - 1+\sin^2 \theta (1-Z^2)\}] = 0\](17)式から
\[1-Z^2 = 1- \frac{(v_1^2 -v_{A1}^2)^2}{(v_1^2 -v_{A1}^2 X)^2} X^2 = \frac{v_1^4 (1-X^2) + 2 v_{A1}^2 v_1^2 (X-1) X}{(v_1^2 -v_{A1}^2 X)^2} = v_1^2 (X-1) \frac{- v_1^2 (X+1) +2 v_{A1}^2 X}{(v_1^2 -v_{A1}^2 X)^2}\]と計算できるので
\[\begin{aligned} &v_1^2 \cos^2 \theta (X-1)+ \frac{1}{2} X v_{A1}^2 \sin^2 \theta v_1^2 (X-1) \frac{- v_1^2 (X+1) +2 v_{A1}^2 X}{(v_1^2 -v_{A1}^2 X)^2} \\ & \quad + \frac{1}{2\gamma} \left[2 C_{s1}^2 X(1-X) - v_1^2 (\gamma-1) \left\{ X^2 -1 + \sin^2 \theta v_1^2 (X-1) \frac{2 v_{A1}^2 X- v_1^2 (X+1)}{(v_1^2 -v_{A1}^2 X)^2}\right\} \right] = 0 \end{aligned}\]上式において\(X=1\)の解は衝撃波のない自明な解なので、以下では\(X \neq 1\)で考えます。よってこの両辺を\(X-1\)で割ることで
\[\begin{aligned} &2 \gamma v_1^2 \cos^2 \theta + \gamma X v_{A1}^2 \sin^2 \theta v_1^2 \frac{- v_1^2 (X+1) +2 v_{A1}^2 X}{(v_1^2 -v_{A1}^2 X)^2} - 2 C_{s1}^2 X \\ & \quad - v_1^2 (\gamma-1) \left\{ X +1 + \sin^2 \theta v_1^2 \frac{2 v_{A1}^2 X- v_1^2 (X+1)}{(v_1^2 -v_{A1}^2 X)^2}\right\} = 0 \end{aligned}\]を得ます。さらに両辺に\((v_1^2-v_{A1}^2 X)^2\)をかけてさらに変形を進めます。
\[\begin{aligned} &(v_1^2-v_{A1}^2 X)^2 \{2 \gamma v_1^2 \cos^2 \theta - 2C_{s1}^2 X - v_1^2 (\gamma-1) (X+1) \} + \{ 2 v_{A1}^2 X- v_1^2 (X+1)\} \\ &\quad + \{ 2 v_{A1}^2 X - v_1^2 (X+1)\} \{ \gamma X v_{A1}^2 v_1^2 \sin^2 \theta - v_1^4 (\gamma-1) \sin^2 \theta\} = 0 \end{aligned}\]第二項の整理から進めましょう。
\[\begin{aligned} (第2項) &= \{ 2 v_{A1}^2 X - v_1^2 (X+1)\} \{ \gamma X v_{A1}^2 - v_1^2 (\gamma-1) \} v_1^2 \sin^2 \theta \\ &= \{ 2 \gamma X^2 v_{A1}^4 - 2 v_{A1}^2 v_1^2 X (\gamma-1) -\gamma X (X+1) v_1^2 v_{A1}^2 + v_1^4 (\gamma-1) (X+1)\} \end{aligned}\]ここで\(\alpha = v_1^2 - v_{A1}^2 X\)として、\(v_1^4\)を無理矢理ここから作り出して整理します。
\[\alpha^2 = v_1^4 - 2 v_1^2 v_{A1}^2 X + v_{A1}^4 X^2 \ \Longrightarrow \ v_1^4 = \alpha^2 + 2 v_1^2 v_{A1}^2 X - X^2 v_{A1}^4\]これを用いると
\[\begin{aligned} (第2項) &= \{ 2 \gamma v_{A1}^2 X^2 - 2 v_1^2 v_{A1}^2 (\gamma-1) X - (\gamma X + \gamma) v_1^2 v_{A1}^2 X + (\gamma-1)(X+1) \alpha^2 \\ & \qquad + 2 v_1^2 v_{A1}^2 (\gamma-1) (X+1) - v_{A1}^4 (\gamma-1)X^2 (X+1)\} v_1^2 \sin^2 \theta \\ &= [\{ 2\gamma - (\gamma-1)(X+1) \} v_{A1}^4 X^2 + \{ -2(\gamma-1) - (\gamma X + \gamma) + 2(\gamma-1) (X+1)\} v_1^2 v_{A1}^2 X \\ & \qquad + (\gamma-1)(X+1) \alpha^2] v_1^2 \sin^2 \theta \\ &= \{(\gamma-\gamma X + X+1) v_{A1}^4 X^2 + (\gamma X -2X-\gamma) v_1^2 v_{A1}^2 X + (\gamma -1)(X+1) \alpha^2\} v_1^2 \sin^2 \theta \end{aligned}\]となります。以上から元の式は
\[\begin{aligned} &\alpha^2 \{2 \gamma v_1^2 \cos^2 \theta - 2C_{s1}^2 X - v_1^2 (\gamma-1) (X+1) \} + \{ 2 v_{A1}^2 X- v_1^2 (X+1)\} \\ & \qquad + \{(\gamma-\gamma X + X+1) v_{A1}^4 X^2 + (\gamma X -2X-\gamma) v_1^2 v_{A1}^2 X + (\gamma -1)(X+1) \alpha^2\} v_1^2 \sin^2 \theta \\ &= \alpha^2 \{ -2 C_{s1}^2 X + (\gamma-\gamma X+X+1) v_1^2 \cos^2 \theta \} + [\{X(1-\gamma)+(\gamma +1)\} v_{A1}^2 X- \{\gamma + X(\gamma-2)\} v_1^2] v_1^2 v_{A1}^2 X \sin^2 \theta = 0 \end{aligned}\]となります。整理すると、磁気流体の斜め衝撃波の圧縮率\(X\)が満たす方程式は
\[\begin{align} &(v_1^2 - v_{A1}^2 X)^2 \left[ C_{s1}^2 X + \frac{1}{2} \{ X(\gamma-1)-(\gamma+1) \} v_1^2 \cos^2 \theta \right] \notag \\ &+ \frac{1}{2} [\{\gamma + X(\gamma-2)\} v_1^2 - \{(\gamma +1) - X(\gamma-1)\} v_{A1}^2 X] v_1^2 v_{A1}^2 X \sin^2 \theta = 0 \tag{20} \end{align}\]を満たし、さらに
\[X = \frac{\rho_2}{\rho_1} = \frac{v_{1x}}{v_{2x}}, \quad \frac{B_{2y}}{B_{1y}} = \frac{v_1^2 - v_{A_1}^2}{v_1^2 - v_{A1}^2 X} X , \quad \frac{P_2}{P_1} = X + \frac{\gamma-1}{2 C_{s1}^2} v_1^2 \left( 1 - \frac{v_2^2}{v_1^2}\right) X \tag{21}\]などを満たします。
Fast shock と slow shock
衝撃波なので\(X > 1\)、すなわち衝撃波面を通過後に流体が圧縮されいる場合を考えましょう。すると\(v_{2x}<v_{1x}\)より、(21)式から\(P_2/P_1>1\)も成り立ちます。これより
\[\frac{B_{2y}}{B_{1y}} = \frac{v_1^2 - v_{A1}^2}{v_1^2 - v_{A1}^2 X} X\]から、以下の2種類の衝撃波が考えられることがわかります。
- \(v_{A1}^2 X > v_{A1}^2 > v_1^2\)のとき、上式から\(B_{2y}/B_{1y}<1\)となります。すなわち衝撃波面に平行な方向の磁場成分が小さくなります。これをslow shockと呼びます。
- \(v_1^2 > v_{A1}^2 X > v_{A1}^2\)のとき、上式から\(B_{2y}/B_{1y}>1\)となります。すなわち衝撃波面に平行な方向の磁場成分が大きくなります。これをfast shockと呼びます。
もう少し定量的に考えてみましょう。(20)式において簡単のため等温(\(\gamma = 1\))、そして\(X \rightarrow 1\)の極限で考えると
\[\begin{aligned} &(v_1^2 - v_{A1}^2) (C_{s1}^2 - v_1^2 \cos^2 \theta) - v_1^2 v_{A1}^4 \sin^2 \theta = 0 \\ &\underbrace{\Longrightarrow}_{\times \cos^2 \theta} \ (v_1^2 - v_{A1}^2) \{ v_{1x}^4 - (C_{s1}^2 + v_{A1}^2) v_{1x}^2 + C_s^2 v_{A1}^2 \cos^2 \theta \} = 0 \end{aligned}\]のようになります。途中\(v_{1x} = v_1 \cos \theta\)を用いました。するとこの解としては
- \(v_1 = v_{A1}\)の解: アルヴェーン波
- \(v_{1x}^4 - (C_{s1}^2 + v_{A1}^2) v_{1x}^2 + C_s^2 v_{A1}^2 \cos^2 \theta=0\)の解: 速い磁気音波と遅い磁気音波
の3つが存在することがわかります。これと垂直磁気流体衝撃波からの類推より、fast shockは\(v_1\)が速い磁気音波の位相速度を超えたときに発生し、slow shockは\(v_1\)が遅い磁気音波の位相速度を超えたときに発生すると考えられます。
ここの厳密な証明の仕方がわかりません...(20)式の3次方程式を解く必要あり?
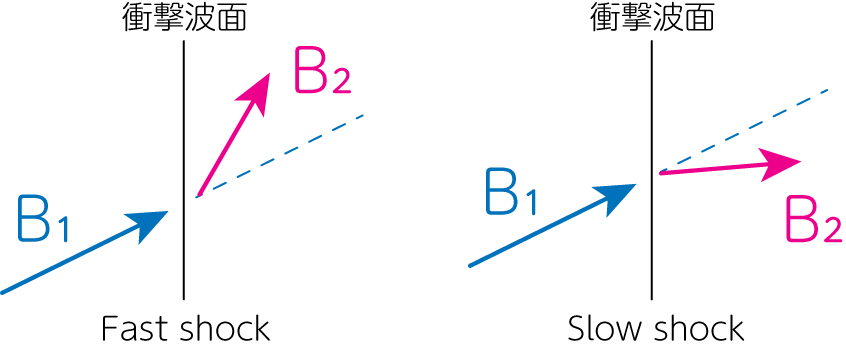
Fast shockは垂直磁気流体衝撃波と同様に、衝撃波面の下流の\(y\)方向磁場は圧縮により強まります(\(B_{2y}>B_{1y})\)。(8)式から磁場の\(x\)成分は変わらないため、磁場の向きが下左図のように変化します。今、流体の速度と磁場が平行な系で物事を考えているため、同時に\(y\)方向の速度も大きくなります(\(v_{2y}>v_{1y}\))。
逆にslow shockは、衝撃波面の下流の\(y\)方向の磁場は弱くなります(\(B_{2y}<B_{1y}\))。よって磁場の向きは下右図のように変化します。同時に\(y\)方向の速度も小さくなります(\(v_{2y}<v_{1y}\))。
\(v_1 = v_{A1}\)の解が表す衝撃波(fast shockとslow shockの中間のため、中間衝撃波とも呼ばれることがあります)の詳細な議論は、後ほど行います。
不連続面
ここでは\(B_x \rightarrow 0\)の極限を考えましょう。先程の図からわかるように、fast shockは垂直磁気流体衝撃波に近づきます。一方、slow shockは\(v_{1x}=v_{2x}=B_{1x}=B_{2x}=0\)から、波面を挟んで\(v_y, B_y\)の値が異なるだけの不連続面となります。このとき
\[P_1 + \frac{1}{8\pi} B_{1y}^2 = P_2 + \frac{1}{8\pi} B_{2y}^2\]のようなガス圧と磁気圧による圧力平衡さえ成り立っていれば良く、\(v_y, B_y\)は任意の値を取ります。
そして\(B_{1x} = B_{2x} \neq 0\)で、流れのない\(v_{1x} = v_{2x} = 0\)のような場合を考えましょう。速度・磁場・圧力は連続ですが、密度と温度は不連続でも構わないような接触不連続面(constact or entropy discontinuity)が考えられます。
スイッチオフ衝撃波
\(v_1 \rightarrow v_{A1}\)の極限で発生する磁気流体斜め衝撃波について考えましょう。\(X \neq 1\)と(16)式
\[\frac{B_{2y}}{B_{1y}} = \frac{v_1^2 - v_{A1}^2 }{v_1^2 - v_{A1}^2 X} X\]から、\(B_{1y} \neq 0\)であっても、\(B_{2y}=0\)となるような衝撃波の存在が示唆されます。下図のように磁場の\(y\)方向が消える(スイッチがオフになる)ことから、これをスイッチオフ衝撃波(switch-off shocks)と呼びます。 今、考えている極限から、この衝撃波は\(v_{1x} = v_{A1, x} = \sqrt{B_{1x}^2 / 4\pi \rho_1}\)のアルヴェーン速度で伝播していくことがわかります。スイッチオフ衝撃波の様子を以下に示します。
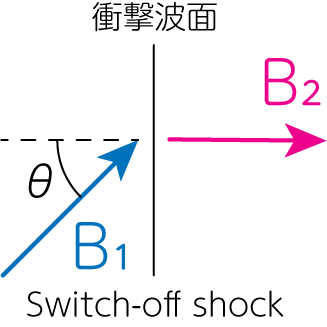
このスウィッチオフ衝撃波の圧縮率を定量的に議論をするために、(20)式において\(v_1 = v_{A1}, X \neq 1\)として整理をしていきましょう。
\[\begin{aligned} &v_{A1}^4 (1-X)^2 \left[ C_{s1}^2 + \frac{1}{2} \{X(\gamma-1) - (\gamma+1)\} v_{A1}^2 \cos^2 \theta\right] \\ & \qquad + \frac{1}{2} [\{ \gamma + X(\gamma-2)\} v_{A1}^2 - \{(\gamma+1) - X(\gamma-1)\} X v_{A1}^2] v_{A1}^4 X \sin^2 \theta = 0 \end{aligned}\]両辺に\(2/v_{A1}^6\)をかけます。このとき、\(A \equiv C_{s1}^2 / v_{A1}^2\)と置いて式変形をしましょう。すると
\[(1-X)^2 [2 XA + \{ X(\gamma-1) - (\gamma+1) \}\cos^2 \theta] + \{ \gamma(1-X)^2 + X (1-X)\} X \sin^2 \theta = 0\]となります。今、\(X \neq 1\)を考えているので、両辺を\(1-X\)で割り、計算を進めると
\[f(X) \equiv (2A + \gamma -1) X^2 - \{ 2A + \gamma(1+\cos^2 \theta) \} X + (\gamma+1) \cos^2 \theta = 0 \tag{22}\]\((2A+\gamma -1)\)は\(A = C_{s1}^2 / v_{A1}^2 > 0, \gamma > 1\)より、常に正です。よって\(f(X)\)は下に凸の2次関数であると分かります。\(f(X) = 0\)の解は
\[X = \frac{2A + \gamma(1+\cos^2 \theta) \pm \sqrt{\{ 2A + \gamma (1+\cos^2 \theta)\}^2 - 4 (2A + \gamma-1) (\gamma+1) \cos^2 \theta}}{2 (2A + \gamma -1)}\]です。一般的な角度\(\theta\)について考察するのは難しいので、2つの極限について考えましょう。
\(\theta \rightarrow 0\)のとき
\[\begin{align} X &= \frac{2A + 2\gamma \pm \sqrt{(2A + 2\gamma)^2 - 4(2A + \gamma-1) (\gamma+1)}}{2 (2A + \gamma-1)} = \frac{A + \gamma \pm \sqrt{A^2 - 2A + 1}}{2A + \gamma-1} \notag \\ &= 1 \quad \mathrm{or} \quad \frac{\gamma + 1}{2A + \gamma-1} \tag{23} \end{align}\]続いて、\(\theta \rightarrow \pi/2\)のとき
\[X = \frac{2A + \gamma \pm (2A + \gamma)}{2 (2A + \gamma-1)} = 0 \quad \mathrm{or} \quad \frac{2A+\gamma}{2A+\gamma-1} \tag{24}\]のようになります。\(X =\rho_2 / \rho_1 = 0\)の解は衝撃波として不適切な解なので、考えないことにします。ここまでは\(A = C_{s1}^2 / v_{A1}^2\)について何も言及してきませんでしたが、(23), (24)式を見ると、\(A > 1, 0 < A<1\)で解の様子が変化することがわかります。
\(A > 1\)のとき、すなわち音速の方が大きいとき、(23)式から\(\theta \rightarrow 0\)の解の一つは
となり、衝撃波として適当な解でありません。よってこのとき\(\theta = 0 \rightarrow \pi / 2\)と増加するとともに、\(X = 1 \rightarrow \frac{2A + \gamma}{2A+ \gamma-1}\)のように増加します。
次は\(1/2 < A < 1\)の場合です。(23), (24)式より
となり、\(\theta = 0\rightarrow \pi/2\)と増加するとともに、\(X = \frac{\gamma+1}{2A+\gamma-1} \rightarrow \frac{2A+\gamma}{2A+\gamma-1}\)のように増加します。
最後は\(0<A<1/2\)の場合です。(23), (24)式より
となり、\(\theta=0 \rightarrow \pi/2\)と増加するとともに、\(\frac{\gamma+1}{2A+\gamma-1} \rightarrow \frac{2A+\gamma}{2A+\gamma-1}\)のように減少します。
スイッチオン衝撃波
今度は衝撃波面が磁場に沿って伝播していく場合を考えましょう(すなわち\(B_{1y}, \theta = 0\)です)。(20)式より
\[(v_1^2 - v_{A1}^2 X)^2 \left[ \frac{1}{2} \{X(\gamma-1)-(\gamma+1)\} v_1^2 \right] = 0\]\(\theta=0\)なので、先程まで議論していたスイッチオフ衝撃波(slow shocks)の解はすでに除外されています。また上式の\([\cdots]\)から出てくるのは磁場なしの垂直衝撃波の解です。そして\((v_1^2 - v_{A1}^2 X)^2 = 0\)から出てくるのがfast shocksに対応する解となります。このときの圧縮率は
\[X = \frac{v_1^2}{v_{A1}^2} \tag{25}\]となります。衝撃波は\(X>1\)なので、この衝撃波が発生する条件は\(v_1 > v_{A1}\)です。さらに今、磁場に沿って衝撃波面が伝播していく状況を考えているので、(8)式と合わせて
\[B_{2x} = B_{1x}, \quad B_{1y} = 0 \tag{26}\]です。(2)式より
\[\begin{aligned} P_2 &= \rho_1 v_{1x}^2 - \rho_2 v_{2x}^2 + P_1 - \frac{1}{4\pi} B_{1x}^2 + \frac{1}{8\pi} B_1^2 + \frac{1}{4\pi} B_{2x}^2 - \frac{1}{8\pi} B_2^2 \\ &= \rho_1 v_{1x}^2 \left( 1-\frac{1}{X}\right) + P_1 - \frac{1}{8\pi} B_{2y}^2 = \rho_1 v_{1x}^2 \left( 1-\frac{1}{X}\right) + P_1 - \frac{1}{8\pi} B_{1x}^2 C \end{aligned}\]のように変形できます。ここで\(C \equiv B_{2y}^2 / B_{1x}^2 = B_{2y}^2 / B_{2x}^2\)のように定義しました。さらに\(\mathbf{v} \parallel \mathbf{B}\)から\(\mathbf{j} = \mathbf{v} \times \mathbf{B} / c = \mathbf{0}\)であることと(7)式より
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1}P_1\right) v_{1x} = \left( \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma-1} P_2 \right) v_{2x}\]ここに(26)式を代入することで
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1\right) X = \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma-1} \left\{ \rho_1 v_{1x}^2 \left( 1-\frac{1}{X}\right) + P_1 - \frac{1}{8\pi} B_{2x}^2 C\right\}\]を得ます。さらに(11)式より
\[v_2^2 = v_{2x}^2 + v_{2y}^2 = v_(2x)^2 + \underbrace{\frac{B_{2y}^2}{B_{2x}^2}}_{=C} v_{2x}^2 \underbrace{=}_{(12)} v_{2x}^2 (1+C) = \frac{v_{1x}^2}{X^2} (1+C)\]となります。これを用いると
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1\right) X = \frac{1}{2} \rho_1 X \frac{v_{1x}^2}{X^2} (1+C) + \frac{\gamma}{\gamma-1} \left\{ \rho_1 v_{1x}^2 \left( 1-\frac{1}{X}\right) + P_1 - \frac{1}{8\pi} B_{1x}^2 C\right\}\]両辺に\(X\)をかけると
\[\begin{aligned} &\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1\right) X^2 = \frac{1}{2} \rho_1 v_{1x}^2 (1+C) + \frac{\gamma}{\gamma-1} \left\{ \rho_1 v_{1x}^2 ( X-1) + P_1 X - \frac{1}{8\pi} B_{1x}^2 C X\right\} \\ &\Longrightarrow \ \frac{\gamma}{\gamma-1} P_1 X(1-X) - \left( \frac{\gamma}{\gamma-1} \frac{1}{8\pi} B_{1x}^2 X - \frac{1}{2} \rho_1 v_{1x}^2 \right) C + \frac{\gamma}{\gamma-1} \rho_1 v_{1x}^2 (X-1) + \frac{1}{2} \rho_1 v_{1x}^2 - \frac{1}{2} \rho_1 v_{1x}^2 X^2 = 0 \end{aligned}\]となります。ここで(25)式と、今は\(v_{1y}=0\)より\(v_1 = v_{1x}\)であること、さらに\(v_{A1}^2 = v_{A1, x}^2 = B_{1x}^2 / 4\pi \rho_1\)であることを用いると
\[\frac{\gamma}{\gamma-1} P_1 X(1-X) - \left( \frac{\gamma}{\gamma-1} \frac{1}{8\pi} B_{1x}^2 - \frac{1}{2} \frac{B_{1x}^2}{4\pi} \right)X C + \frac{\gamma}{\gamma-1} X \frac{B_{1x}^2}{4\pi} (X-1) + \frac{1}{2} X \frac{B_{1x}^2}{4\pi} - \frac{1}{2} X \frac{B_{1x}^2}{4\pi} X^2 = 0\]これを整理して
\[\begin{aligned} &\frac{\gamma}{\gamma-1} P_1 X (1-X) - \frac{1}{\gamma-1} \frac{B_{1x}^2}{8\pi} X C + \frac{2\gamma}{\gamma-1} \frac{B_{1x}^2}{8\pi} X (X-1) + \frac{B_{1x}^2}{8\pi} X (1-X^2) = 0 \\ &\Longrightarrow \ \frac{8\pi \gamma}{B_{1x}^2} P_1 (1-X) - C + 2 \gamma (X-1) + (\gamma-1) (1-X)(1+X) = 0 \end{aligned}\]よって
\[C = \frac{B_{2y}^2}{B_{1x}^2} = (X-1) \left\{ (\gamma+1)- (\gamma-1) X- \frac{8\pi \gamma}{B_{1x}^2} P_1 \right\} \tag{27}\]今、\(X > 1\)を考えているので、\(B_{2y}^2 >0\)となるには\(\{\cdots \} >0\)となる必要があります。再び音速\(C_s^2 = \gamma P / \rho\)とアルヴェーン速度\(v_{A}^2 = B^2 / 4\pi \rho\)を用いて整理すると
\[(\gamma+1)- (\gamma-1) X- \frac{2C_{s1}^2}{v_{A1}^2} > 0 \ \Longrightarrow \ 1 < X < \frac{\gamma + 1 - \frac{2 C_{s1}^2}{v_{A1}^2}}{\gamma-1} \tag{28}\]のようになります。(28)式の圧縮率を満たすような磁場に沿った衝撃波が存在する場合、それは(27)から\(B_{2y} \neq 0\)となります。これは下図のように、\(B_{1y} = 0\)から衝撃波通過後には\(y\)方向磁場が出現する(スイッチがオンになる)ことから、スイッチオン衝撃波(switch-on shocks)と呼ばれます。
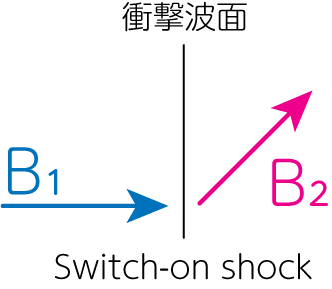
(28)式から、スイッチオン衝撃波の場合の圧縮率は最大でも\(\frac{\gamma+1}{\gamma-1} \ (v_{A1} \gg C_{s1})\)までです。さらに(28)式の最右辺が1より大きくなる(スイッチオン衝撃波が発生する)条件は、大雑把に\(v_{A1} > C_{s1}\)と見積もることができます。すなわちこの衝撃波が起こるのはアルヴェーン速度が音速を上回るような、磁場が卓越した領域に限られます。
最後に(27)式の右辺から、スイッチオン衝撃波での磁力線の折れ曲がり角の最大値を計算しましょう。(27)式右辺を\(g(X)\)とすると
\[\begin{align} g(X) &= - (\gamma - 1) X^2 + 2 \left( \gamma - \frac{C_{s1}^2}{v_{A1}^2}\right) X - \gamma -1 + \frac{2 C_{s1}^2}{v_{A1}^2} \notag \\ &= - (\gamma -1) \left( X - \frac{\gamma - \frac{C_{s1}^2}{v_{A1}^2}}{\gamma-1}\right)^2 + \frac{\left( \frac{C_{s1}^2}{v_{A1}^2}-1\right)^2}{\gamma-1} \tag{29} \end{align}\]よってこの式は上に凸の2次関数であり、\(X = \frac{\gamma - \frac{C_{s1}^2}{v_{A1}^2}}{\gamma-1}\)のとき、磁力線の折れ曲がりが最大となることがわかります。
中間衝撃波
(20)式は\(v_1 = v_{A1}\)かつ\(X=1\)の場合にも成り立ちます。すなわち(20)式から\(v_{1x}=v_{2x}\)の場合にも成り立つのです。これは一見すると、(16), (17)式は分子・分母ともに0となるため、物理的な意味を成さないように見えるかもしれません。しかし、基礎方程式である(9)式から計算を進めてみると
\[\begin{align} &v_{1x} B_{1y} - v_{1y} B_{1x} = \underbrace{v_{2x}}_{=v_{1x}} B_{2y} - v_{2y} \underbrace{B_{2x}}_{(8)} \notag \\ &\Longrightarrow \ \frac{B_{2y}}{B_{1y}} = 1 + \frac{v_{2y} -v_{1y}}{v_{1x}} \frac{B_{1x}}{B_{1y}} \underbrace{=}_{(10)} 1 + (v_{2y}-v_{1y}) \frac{B_{1y}}{B_{1x} v_{1y}}\frac{B_{1x}}{B_{1y}} = \frac{v_{2y}}{v_{1y}} \tag{30} \end{align}\](2), (8)式と、今考えている\(X=\rho_2 / \rho_1 = v_{1x} / v_{2x} =1\)より
\[P_1 + \frac{1}{8\pi} B_{1y}^2 = P_2 + \frac{1}{8\pi} B_{2y}^2 \tag{31}\]そして(7), (8)式より
\[\frac{1}{2} \rho_1 v_1^2 v_{1x} + \frac{\gamma}{\gamma-1} P_1 v_{1x} + \frac{1}{4\pi} B_1^2 v_{1x} - \frac{1}{4\pi} v_{1y} B_{1y} B_{1x} = \frac{1}{2} \rho_1 v_2^2 v_{1x} + \frac{\gamma}{\gamma-1} P_2 v_{1x} + \frac{1}{4\pi} B_2^2 v_{1x} - \frac{1}{4\pi} v_{2y} B_{2y} B_{1x}\]これを整理すると
\[\begin{align} \frac{\gamma}{\gamma-1} (P_1 - P_2) v_{1x} &= \frac{1}{2} \rho_1 (v_{2y}^2 - v_{1y}^2) v_{1x} + \frac{1}{4\pi} (B_{2y}^2 - B_{1y}^2) v_{1x} - \frac{1}{4\pi} B_{1x} (v_{2y} B_{2y} - v_{1y} B_{1y}) \notag \\ &\underbrace{=}_{(30)} \frac{1}{2} \rho_1 \left( \frac{B_{2y}^2}{B_{1y}^2} - 1 \right) v_{1y}^2 v_{1x} + \frac{1}{4\pi} ( B_{2y}^2 - B_{1y}^2 ) v_{1x} - \frac{1}{4\pi} \underbrace{B_{1x}}_{(10)} \left( \frac{B_{2y}}{B_{1y}} v_{1y} B_{2y} - v_{1y} B_{1y}\right) \notag \\ &= \frac{1}{2} \rho_1 \left( \frac{B_{2y}^2}{B_{1y}^2} - 1 \right) v_{1y}^2 v_{1x} \tag{32} \end{align}\]以上、(31), (32)式より
\[\left( \frac{1}{8\pi} \frac{\gamma}{\gamma-1} - \frac{1}{2} \rho_1 \frac{v_{1y}^2}{B_{1y}^2} \right) (B_{2y}^2 - B_{1y}^2) = 0 \tag{33}\]この式から\(B_{2y} = - B_{1y}, v_{1y} = -v_{2y}\)のような解が存在することがわかります(\(B_{2y} = B_{1y}, v_{1y} = v_{2y}\)は何も変わっていない解なので考えません)。これは下図のように、この波面を境に磁場と速度の\(y\)成分のみが反転していることから、回転不連続面(rotational discontinuity)と呼ばれています。速い磁気音波と遅い磁気音波の中間であるアルヴェーン速度で伝播していくことから、これを中間衝撃波(intermediate shocks)と呼ぶこともあります。しかし、普通の衝撃波と異なり、密度と圧力には不連続が生じていないことに注意しましょう。
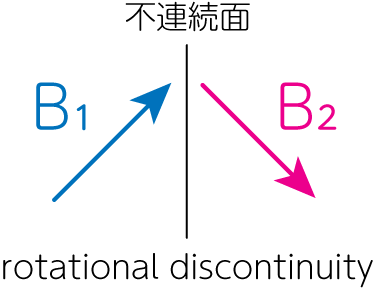
実際に1.5次元の磁気流体衝撃波管(MHD shock tube)問題を数値的に解くと、この不連続部分で密度の不連続が発生することが知られています。これは数値的な粘性など散逸が無視できない系特有のものと考えられていますが、この回転不連続面の性質やその安定性についてはまだまだ議論の余地があります。というのも保存則を用いて導出される衝撃波のジャンプ条件(磁気流体的なランキン・ユゴニオ条件)による解は、その磁気流体の内部構造(内部状態)を無視しているため、そうして得られた解が物理的かどうかを常に判別する必要があります。またその判別法は完璧ではなく、特に磁気流体の教科書には非物理的と書かれている中間衝撃波の解がその後の詳細な定式化で否定されることもあるからです。
近いうちに簡単なMHD計算コードを作成して、MHD shock tubeの結果も掲載したいです (><)
参考文献
[1] Priest, “Solar Magnetohydrodynamics”
[2] 草野完也, “宇宙における高速流と衝撃波研究の最前線, 太陽フレアにおける高速流とスローショック”
[3] Inoue & Inutsuka, 2007, “Evolutionary Conditions in Dissipative MHD Systems Revisited”