Table of contents
ビリアル定理
ここでは重力多体系を考える上で重要なビリアル定理についてメモしています。
導出
それぞれの天体の質量を\(m_j\)、位置を\(\mathbf{r}_j\)、運動量を\(\mathbf{p}_j\)とします。以下の数式を変形していきましょう。
\[\frac{d}{dt} \left( \sum_j \mathbf{p}_j \cdot \mathbf{r}_j \right) = \sum_{j} \left\{ \frac{d\mathbf{p}_j}{dt} \cdot \mathbf{r}_j + \mathbf{p}_j \cdot \frac{d \mathbf{r}_j}{dt} \right\} \tag{1}\]ここでそれぞれの天体に働く力を\(\mathbf{F}_j\)、そして速度を\(\mathbf{v}_j\)とすると、\(\frac{d \mathbf{p}_j}{dt} = \mathbf{F}_j, \frac{d \mathbf{r}_j}{dt} = \mathbf{v}_j\)より
\[\frac{d}{dt} \left( \sum_j \mathbf{p}_j \cdot \mathbf{r}_j \right) = \sum_j (\mathbf{F}_j \cdot \mathbf{r}_j + \mathbf{p}_j \cdot \mathbf{v}_j) \underbrace{=}_{\mathbf{p}_j = m_j \mathbf{v}_j} \sum_j \mathbf{F}_j \cdot \mathbf{r}_j + 2 \sum_j \frac{1}{2} m_j \mathbf{v}_j^2 \tag{2}\]系全体の運動エネルギーを
\[\mathcal{T} = \sum_j \frac{1}{2} m_j \mathbf{v}_j^2 \tag{3}\]のように書くと、(2)式から
\[\frac{d}{dt} \left( \sum_j \mathbf{p}_j \cdot \mathbf{r}_j \right) = 2 \mathcal{T} + \sum_j \mathbf{F}_j \cdot \mathbf{r}_j \tag{4}\]のようになります。この式の時間平均をとりましょう。
\[(左辺) = \frac{1}{\tau} \int_0^\tau dt \frac{d}{dt} \left( \sum_j \mathbf{p}_j \cdot \mathbf{r}_j \right) = \frac{1}{\tau} \left[ \sum_j \mathbf{p}_j \cdot \mathbf{r}_j \right]_0^\tau\] \[(右辺) = 2 \langle \mathcal{T}\rangle + \langle \sum_j \mathbf{F}_j \cdot \mathbf{r}_j \rangle\]\(\langle \cdots \rangle\)は時間平均操作を表します。 ここで、この多体系が常に保たれ続けること(すなわち天体が抜け出したりせず、系全体のエネルギーが有限であり続けると)仮定しましょう。 この仮定より\(\mathbf{p}_j, \mathbf{r}_j\)は全て有限の値を持つと考えて良いので、\(\tau \rightarrow \infty\)のとき左辺はゼロになります。以上より
\[2 \langle \mathcal{T}\rangle + \langle \sum_j \mathbf{F}_j \cdot \mathbf{r}_j \rangle = 0 \tag{5}\]と求まります。さらに系全体のポテンシャルエネルギーを
\[\mathcal{V} = \frac{1}{2} \sum_i \sum_{j\neq i} V (\vert \mathbf{r}_i - \mathbf{r}_j\vert) \tag{6}\]のように書くことにします。ポテンシャルエネルギーが\(V(\vert \mathbf{r}_i - \mathbf{r}_j \vert) \propto \vert \mathbf{r}_i - \mathbf{r}_j \vert^n\)のように書かれるとき、 適当な定数\(a\)に対して\(V(a \vert \mathbf{r}_i - \mathbf{r}_j \vert) = a^n V(\vert \mathbf{r}_i - \mathbf{r}_j \vert)\)のように書くことができます。 これを利用すると、(6)式から
\[\mathcal{V}(a \vert \mathbf{r}_i - \mathbf{r}_j \vert) = \frac{1}{2} \sum_i \sum_{j\neq i} V(a\vert \mathbf{r}_i - \mathbf{r}_j \vert) = \frac{a^n}{2} \sum_i \sum_{j\neq i} V(\vert \mathbf{r}_i - \mathbf{r}_j \vert) = a^n \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) \tag{7}\]のように変形することができます。この式を\(a\)で微分すると
\[(最左辺) = \frac{\partial}{\partial a} \mathcal{V} (a \vert \mathbf{r}_i - \mathbf{r}_j \vert) = \sum_k \frac{\partial (a \mathbf{r}_k)}{\partial a} \frac{\partial}{\partial (a \mathbf{r}_k)} \mathcal{V} (a \vert \mathbf{r}_i - \mathbf{r}_j \vert) = \sum_k \mathbf{r}_k \cdot \frac{\partial}{\partial (a \mathbf{r}_k)} \mathcal{V} (a \vert \mathbf{r}_i - \mathbf{r}_j \vert)\] \[(最右辺) = n a^{n-1} \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert)\]を得ます。\(a\)は適当な定数であるため、\(a=1\)としても差し支えありません。すると
\[n \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) = \sum_k \mathbf{r}_k \cdot \frac{\partial}{\partial \mathbf{r}_k} \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) \tag{7}\]また、ここから
\[\frac{\partial}{\partial \mathbf{r}_k} \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) = \frac{1}{2} \frac{\partial}{\partial \mathbf{r}_k} \left\{ \sum_i \sum_{j\neq i} V(\vert \mathbf{r}_i - \mathbf{r}_j \vert) \right\} = \frac{\partial}{\partial \mathbf{r}_k} \sum_{k \neq \ell} V(\vert \mathbf{r}_k - \mathbf{r}_\ell \vert) = - \sum_{\ell \neq k} \mathbf{F}_{k\ell} = - \mathbf{F}_k\]のように計算されます。\(\mathbf{F}_{k\ell}\)は\(k\)番目の天体が\(\ell\)番目の天体から受ける力です。以上より
\[\frac{\partial}{\partial \mathbf{r}_k} \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) = - \mathbf{F}_k \tag{8}\]となります。(7), (8)式より
\[n \mathcal{V} (\vert \mathbf{r}_i - \mathbf{r}_j \vert) = - \sum_k \mathbf{r}_k \cdot \mathbf{F}_k \tag{9}\](9)式を(5)式に代入すれば
\[2 \langle \mathcal{T} \rangle - n \langle \mathcal{V} \rangle = 0 \ \Longrightarrow \ \langle \mathcal{T} \rangle = \frac{n}{2} \langle \mathcal{V} \rangle \tag{10}\]というビリアル定理 (Virial theorem)を得ることができます。
ビリアル定理から導かれる、重力多体系の安定性
(10)式では\(n\)をそのまま残しました。 これは位置\(\mathbf{r}\)でのポテンシャル\(\mathcal{V} (\mathbf{r})\)が\(\vert \mathbf{r} \vert^n\)に比例するとしたときの\(n\)です。 重力ポテンシャルの場合、その依存性は\(n = -1\)となります。ここではその\(n\)によって系がどのように振る舞うかを見てみましょう。 系全体のエネルギーの長時間平均は
\[\langle E \rangle = \langle \mathcal{T} \rangle + \langle \mathcal{V} \rangle \tag{11}\]なので、(10), (11)式より
\[\langle E \rangle = \left(1 + \frac{2}{n} \right) \langle \mathcal{T} \rangle \tag{12}\]\(\langle \mathcal{T} \rangle\)は運動エネルギーであるため、常に0以上の値を持ちます。 よって\(n < -2\)のとき\(\langle E\rangle > 0\)となり、これはこの系のポテンシャルから抜け出して無限遠に飛び去ることができる(ポテンシャルエネルギーが0となる無限遠でも、ゼロでない運動エネルギーを持つ)ことを意味します。 よって\(n < -2\)のポテンシャルが作る多体系は、系として安定に存在することができません。 一方、重力ポテンシャルの場合、\(n = -1\)から、安定に存在することができます。
応用: 銀河団などの質量推定
ビリアル定理を用いて、実際の重力多体系の総質量を推定する方法をご紹介します。銀河団などの天体が生まれてから十分時間が経過しており、系が安定な状態に落ち着いていると仮定すると
\[\langle \mathcal{T} \rangle \simeq \mathcal{T} = \frac{1}{2} \sum_j m_j v_j^2 \tag{13}\]が成り立っていると考えて良いでしょう。銀河団を構成する銀河の速度の2乗質量平均(速度分散)
\[\bar{v^2} = \frac{\sum_j m_j v_j^2}{\sum_j m_j} \tag{14}\]と銀河団の総質量\(M = \sum_j m_j\)を用いると、(13)式は
\[\langle \mathcal{T} \rangle \simeq \frac{1}{2} M \bar{v^2} \tag{15}\]のように書き換えることができます。一方、系全体の重力ポテンシャルエネルギーは、系の典型的な半径を\(R\)とすれば
\[\langle V \rangle \simeq - \frac{GM^2}{R} \tag{16}\]程度と考えることができます。
(15), (16)式、そして(10)式に\(n = -1\)を代入したものを用いると
\[\frac{1}{2} M \bar{v^2} = \frac{1}{2} \frac{G M^2}{R} \ \Longrightarrow \ \bar{v^2} = \frac{GM}{R} \ \Longrightarrow \ M_V = \frac{R \bar{v}^2}{G} \tag{17}\]と求まります。このように、ビリアル定理を利用して求められる重力多体系の質量をビリアル質量\(M_V\)と呼びます。 観測から\(M_V\)を求めるには\(R, \bar{v}^2\)を求める必要があります。例えば遠くの銀河団の場合には、下図のような状況を考えます。
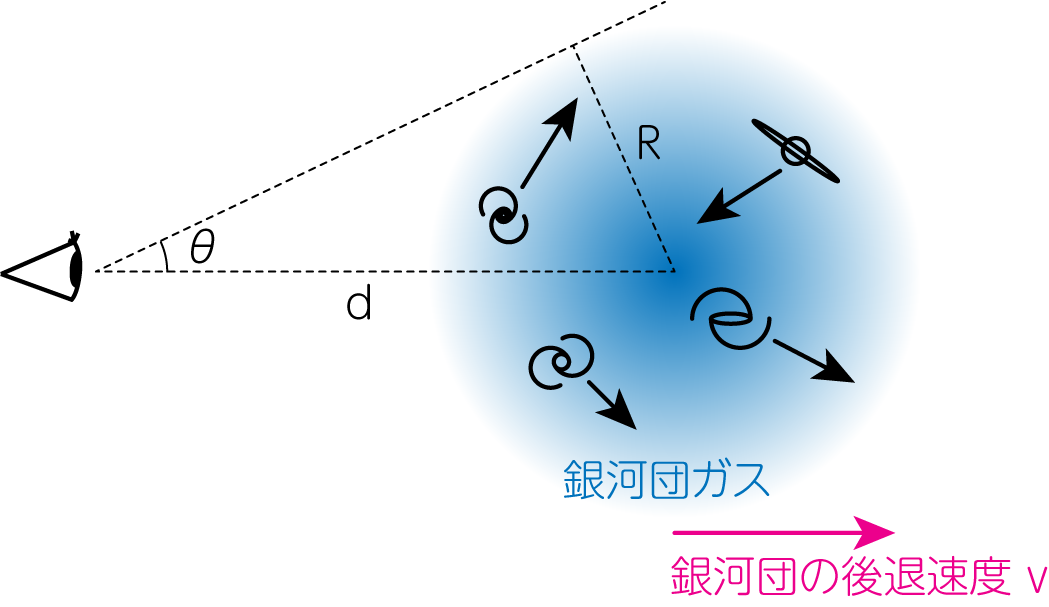
分光観測から赤方偏移\(z\)を決定することで、銀河団全体が遠ざかる速度\(v\)が得られます。するとハッブルの法則より、距離\(d\)が求まります。 この値と、銀河団を見込む角度\(\theta\)を利用すれば、銀河団の半径\(R\)が計算されます。 さらに分光観測から個々の銀河の速度を一つ一つ測定することで、銀河の速度の2乗質量平均(速度分散)\(\bar{v^2}\)が求まります。 ただし、個々の銀河を観測したときに求まるのは、視線方向の速度分散\(\bar{v_r^2}\)のみです。 速度分散の他の方向成分をそれぞれ\(\bar{v_\theta^2}, \bar{v_\varphi^2}\)と書き、さらに系が球対称で等方的に運動していると仮定すると
\[\bar{v^2} = \bar{v_r^2} + \bar{v_\theta^2} + \bar{v_\varphi^2} = 3 \bar{v_r^2}\]から、(17)式は
\[M_V = \frac{3 R \bar{v_r^2}}{G} \tag{18}\]これらを用いることで\(M_V\)を求めることが可能です。
もしも近傍にある球状星団などで\(M_V\)を求める場合には、ハッブルの法則のような宇宙論的な効果を用いることができません。よって系の半径は別の方法で求める必要があります。 実は天球面上に投影された見かけの大きさ\(R_\mathrm{proj}\)と、その天体の半径\(R\)の間には
という関係が一般に成り立ちます。これを用いれば、(18)式は
\[M_V = \frac{3 \pi R_\mathrm{proj} \bar{v_r^2}}{2G} \tag{20}\]となります。よって、撮像観測から見かけの大きさ\(R_\mathrm{proj}\)と、分光観測から個々の天体の視線方向の速度分散\(\bar{v_r^2}\)を求めれば、\(M_V\)の推定が可能です。
ダークマターの発見
1933年、Zwickyはかみのけ座銀河団(Coma cluster)に含まれる銀河の運動を観測し、そこから得た速度分散と上述のビリアル定理を用いることで、かみのけ座銀河団の総質量を推定しました。 するとバリオンの総質量(銀河団に含まれる銀河の総質量と、X線を放出している高温の銀河団プラズマ質量の合計)より一桁大きい結果となります。 このことは、我々人類が電磁波では見ることができない質量が存在することを示唆しており、これを今日ではダークマター(dark matter: 暗黒物質)と呼びます。
ダークマターの存在を示唆する他の観測としては、例えば銀河の回転曲線を利用したものがあります。
天の川銀河中心に存在する巨大質量の発見
2020年のノーベル物理学賞に、ブラックホールの理論からはペンローズ博士、そして天の川銀河中心の超巨大コンパクト天体の観測からゲンツェル博士とゲーズ博士が選ばれました。 特に観測の2人は1990年代に天の川銀河中心部の星団(Nuclear Star Cluster: NSC)の観測を行い、その星団のメンバーである恒星の固有運動の速度分散を求めました。 その値を(20)式などに代入することで、銀河中心の数pc領域に\(10^6M_\odot\)の質量が存在することを求めました。天の川銀河中心については以下の記事もご覧ください。
一般相対性理論番外編、天の川銀河中心の超巨大質量コンパクトオブジェクトの発見
参考文献
谷口義明, 岡村定矩, 祖父江義明, “銀河 I”
鶴剛, 宇宙物理学入門講義資料, 第3章: ビリアル定理と自己重力系