Table of contents
3.2 遷移確率
3つのEinstein係数の間には(3.9), (3.10)の関係があるため、1つの係数がわかれば、他の係数を知ることができます。ここでは古典的な概念を使って\(B_{lu}\)の形を導出しましょう。
古典的導出(Rayleigh散乱の考え方)
電磁波が作る電場\({\bf E}_0 e^{i\omega t}\)のもとで、イオンに束縛された電子の振動を考えます。運動方程式は
\[m (\ddot{\bf x} + \omega_0^2 {\bf x}) = -e {\bf E}_0 e^{i\omega t} - m \gamma \dot{\bf x} \tag{3.16}\]のように書けます。ここで\(\omega_0\)は束縛状態の電子の固有振動数で、\(\gamma\)はその状態の減衰係数を表します。束縛状態の電子は、固有振動(振幅\(x_0\), 加速度\(\ddot{x} = \omega_0^2 x_0\))によって電磁波を放出します。Larmorの公式より、毎秒\(\frac{2e^2 \ddot{x}^2}{3c^3}\)のエネルギーを失うことを、減衰係数に対応させます。このエネルギー損失率を速度\(\omega_0 x_0\)に比例する抵抗力がする仕事率と考えて
\[\underbrace{(m \gamma \omega_0 x_0)}_{減衰力} \times \underbrace{(\omega_0 x_0)}_{速度} = \frac{2 e^2 \omega_0^4 x_0^2}{3c^3} \ \Longrightarrow \ \gamma = \frac{2e^2 \omega_0^2}{3m c^3} \tag{3.17}\]となります。
\(x \propto e^{i\omega t}\)として1つの振動数のFourier modeについて(3.16)式を解くと
が得られます。ここから、加速度は
\[\ddot{\bf x} = Re \left[ \frac{\frac{e\omega^2}{m}{\bf E}_0 e^{i\omega t }}{\omega_0^2 - \omega^2 + i \gamma \omega}\right] = \left| \frac{\frac{e\omega^2}{m}}{\omega_0^2 - \omega^2 + i\gamma \omega}\right| {\bf E}_0 \cos (\omega t + \delta) \tag{3.19}\]となります。この振動によって毎秒放出される電磁波のエネルギーの平均値は
\[\langle P \rangle = \langle \frac{2e^2 \ddot{\bf x}^2}{3c^3} \rangle = \frac{2e^4 \omega^4}{3m^2 c^3} \underbrace{\langle \cos^2 (\omega t) \rangle}_{=1/2} \frac{E_0^2}{(\omega^2 - \omega_0^2)^2 + \gamma^2 \omega^2} = \frac{1}{2} \frac{e^2 \omega^2}{m} \frac{\gamma E_0^2}{(\omega^2 - \omega_0^2)^2 + \gamma^2 \omega^2}\]のように表されます。この放射を流入する電磁波の散乱だと考えます。エネルギー流入率は\(\frac{cE_0^2}{8\pi}\)、そして散乱断面積を\(\sigma (\omega)\)と書くと
\[\frac{cE_0^2}{8\pi} \sigma (\omega) = \left( \frac{e^2 \omega^2}{2m}\right) \frac{\gamma E_0^2}{(\omega^2 - \omega_0^2)^2 + \gamma^2 \omega^2} \tag{3.20}\]のように関係づけられます。\(\omega \simeq \omega_0\)の場合に散乱断面積が大きくなるので、そのような場合を考えましょう。
\[(\omega^2 - \omega_0^2)^2 = (\omega - \omega_0)^2 (\omega+ \omega_0)^2 \simeq 4\omega_0^2 (\omega-\omega_0^2) \tag{3.21}\]と書けるので、(3.20)式から
\[\sigma (\omega) = \frac{4\pi e^2 \omega_0^2}{mc} \frac{\gamma}{4\omega_0^2 (\omega-\omega_0)^2 + \gamma^2 \omega_0^2} = \frac{\pi e^2}{mc} \frac{\frac{\gamma}{4\pi^2}}{(\nu - \nu_0)^2 + \left(\frac{\gamma}{4\pi} \right)^2} = \sigma_\nu \tag{3.22}\]が得られます。途中、\(\omega = 2\pi \nu\)の関係を用いました。ここで(3.22)式に現れている式の形は
\[\int_0^\infty \frac{\frac{\gamma}{4\pi^2}}{(\nu-\nu_0)^2 + \left(\frac{\gamma}{4\pi}\right)^2} d\nu \underbrace{=}_{x=\nu-\nu_0} \int_{-\nu_0}^\infty \frac{\frac{\gamma}{4\pi^2}}{x^2 + \left(\frac{\gamma}{4\pi}\right)^2} dx \simeq \int_{-\infty}^\infty \frac{\frac{\gamma}{4\pi^2}}{x^2 + \left(\frac{\gamma}{4\pi}\right)^2} dx = 1 \tag{3.23}\]で、この関数は規格化されたLorentz profile (またはdamping profile)として知られています。(3.23)式の途中の近似は、\(\nu_0\)が光の周波数で十分大きな値であることを用いました。
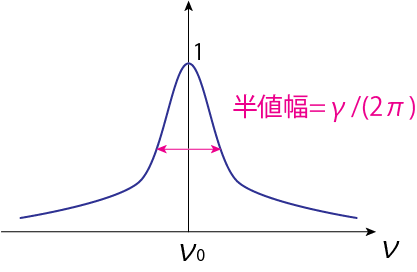
\(\sigma_\nu\)を共鳴振動数\(\nu_0\)の周りで積分すると
\[\sigma_{\rm{tot}} = \int_{-\infty}^\infty \frac{\frac{\gamma}{4\pi^2}}{(\nu-\nu_0)^2 + \left( \frac{\gamma}{4\pi}\right)^2} d(\nu-\nu_0) \underbrace{=}_{\nu-\nu_0 = x = \frac{\gamma}{4\pi}\tan \theta} \frac{\pi e^2}{mc} \tag{3.24}\]となります。このような古典的な取り扱いでは、原子の特徴や遷移するエネルギー準位に依存しない形となります。
量子力学的な取り扱い
量子力学的な考察により得られる断面積はこれとは大きく異なりますが、慣習上、準位\(l\)と\(u\)の間の遷移における断面積は
\[\sigma_{\rm{tot}} = \frac{\pi e^2}{mc} f_{lu} \tag{3.25}\]のように表されます。ここで\(f_{lu}\)はこの遷移の振動子強度(Oscillator strength; f-value)と呼ばれるものです。\(f_{lu}\)は一般的には1より小さな値ですが、非常に強い吸収線に対しては1に近い値を持ちます。
\(\sigma_{\rm{tot}}\)とEinstein係数\(B_{lu}\)とは
の関係を持ちます。
半古典的に求めたOscillator strength
Oscillator strength \(f_{lu}\)の計算は量子力学に基づいて行われます。ここではKramersが主量子数\(n' \rightarrow n\)の遷移に対して半古典的に求めた水素原子のOscillator strength
\[f_K = \frac{32}{3\pi \sqrt{3}} \left( \frac{1}{n'^2} - \frac{1}{n^2} \right)^{-3} \frac{1}{n^3 n'^5} \tag{3.27}\]を用いて
\[f_{n' n} = g_I (n', n) f_K (n', n) \tag{3.28}\]のように表されます。ここで\(g_I (n', n)\)はGaunt factorと呼ばれる1のオーダーの値を持つ補正factorです。
Oscillator strengthの例をご紹介します。\(\rm{H}_\alpha\)では\(f_{23}=0.6407\)、\(\rm{H}_\beta\)に対しては\(f_{24}=0.1193\)、そして\(\rm{H}_\gamma\)に対しては\(f_{25}=0.0447\)などです。\(n\)が大きいほど、散乱断面積が小さいことがわかります。