Table of contents
2 恒星大気中の放射の流れ
第1章では、星から発せられた光のIntensity \(I_\nu\)は地球に届くまで変化しないと仮定しました。これは、恒星から地球までの空間はほぼ真空で、光がその間に吸収・散乱をほとんど受けないためです(正確には星間物質による吸収・散乱を効力する必要があります)。恒星大気や恒星内部では、光とガスとの相互作用により光のIntensityは変化します(大気では光が放出される前に特定の振動数範囲のIntensityが小さくなり、吸収線が作られます)。光のIntensityの変化を司る微分方程式をRadiative transferの式(輻射輸送方程式)と呼びます。
2.1 Radiative Transferの式
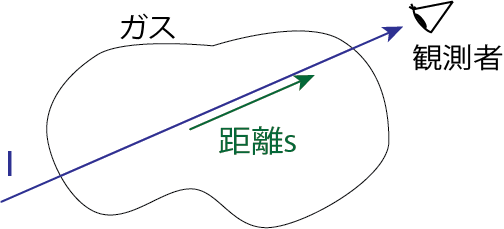
光が進む道筋にそった距離を\(s\)と書くと、光が進むにつれて起こるIntensityの変化は
\[dI_\nu = I_\nu (s + ds) - I_\nu (s) = \eta_\nu (s) \rho(s) ds - (\kappa_\nu (s) + \sigma_\nu (s)) \rho(s) I_\nu (s) ds \tag{2.1}\]または
\[\frac{dI_\nu}{ds} = \eta_\nu \rho - (\kappa_\nu + \sigma_\nu) \rho I_\nu \tag{2.2}\]のように表現されます。ここで\(\eta_\nu\)は発光係数(emission coefficient)またはemissivityと呼ばれるもので、単位質量・単位立体角・単位時間あたりに放出されるエネルギーを表します。また\(\kappa_\nu, \sigma_\nu\)はそれぞれ単位質量あたりの吸収係数と散乱係数(散乱断面積)です。さらに\(\rho\)は質量密度です。
球対称構造を持つ恒星では\(\kappa_\nu, \sigma_\nu, \rho\)などの物理量は中心からの距離\(r\)の関数になります。そのため、\(s\)よりも\(r\)で表現する方が都合が良いです。光の進む方向を天頂角\(\theta\)で表します。光が\(ds\)の方向に進むと、中心からの距離と天頂角が変化するので、微分の連鎖律から
\[\frac{d I_\nu}{ds} = \frac{dr}{ds} \frac{\partial I_\nu}{\partial r} + \frac{d\theta}{ds} \frac{\partial I_\nu}{\partial \theta}\]のように書かれます。
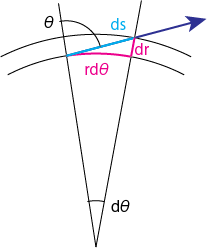
上図より\(dr = ds \cos\theta, -r d\theta = r \Delta \theta = ds \sin\theta\)の関係があるため、(2.2)式は
\[\cos \theta \frac{\partial I_\nu}{\partial r} - \frac{\sin \theta}{r} \frac{\partial I_\nu}{\partial \theta} = \eta_\nu \rho - (\kappa_\nu + \sigma_\nu) \rho I_\nu \tag{2.2'}\]のように表されます。
平行平面(Plane-parallel)近似
多くの場合、恒星大気の厚さ\(D\)は中心からの距離\(R\)に比べて非常に薄いので
\[\left| \frac{\partial I_\nu}{\partial r} \right| \simeq \frac{I_\nu}{D} \gg \frac{1}{r} \left| \frac{\partial I_\nu}{\partial \theta}\right| \simeq \frac{I_\nu}{\pi R}\]の関係が成り立ちます。よって(2.2’)式の左辺第2項は無視できて
\[\cos \theta \frac{d I_\nu}{d\theta} = \eta_\nu \rho - (\kappa_\nu + \sigma_\nu) \rho I_\nu \tag{2.3}\]のようになります。これは平行平面(plane-parallel)近似と言われ、この仮定のもとでは天頂角\(\theta\)は光路にそって変化しません。
光学的深さ (Optical depth)
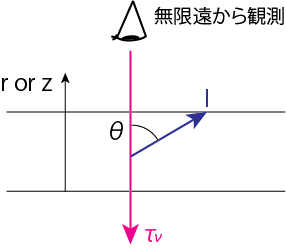
光学的深さ(Optical depth)\(tau_\nu\)を
\[\tau_\nu = \int_r^\infty (\kappa_\nu + \sigma_\nu) \rho dr \quad {\rm or} \quad d\tau_\nu = -(\kappa_\nu + \sigma_\nu) \rho dr \tag{2.4}\]と定義します。\(\tau_\nu\)は表面から遠く離れた\(\rho=0\)の場所で0で、内側に向かって大きくなります。
(2.3)式を\((\kappa_\nu + \sigma_\nu) \rho\)で割って
を得ます。ここで\(\mu = \cos \theta\)、さらに
\[S_\nu = \frac{\eta_\nu}{\kappa_\nu + \sigma_\nu} \tag{2.6}\]は源泉関数(Source funciton)と呼ばれるものです。(2.5)式の右辺は単位面積・単位立体角・単位時間に\(\theta\)方向に流れるエネルギーを表します。
発光係数 (Emission coefficient)
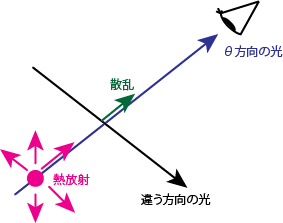
発光係数\(\eta_\nu\)は熱放射の部分\(\eta^t_\nu\)と、他の方向の光が散乱によって\(\theta\)方向に入ってくる\(\eta^s_\nu\)とに分けて
\[\eta_\nu = \eta^t_\nu + \eta^s_\nu \tag{2.7}\]のように書くことができます。
熱放射の部分に対して、局所熱平衡(LTE)を仮定すると、状態が時間的に変化しないためには、単位時間に吸収したエネルギーと同じ量を単位時間に放出しなければならないので、
Kirchhoff-Planck relationが成り立ちます。ここで\(B_\nu (T)\)はプランク関数
\[B_\nu (T) = \frac{2h\nu^3/c^2}{\exp(h\nu/(k_B T))-1}, \ {\rm or} \ B_\lambda (T) = \frac{2hc^2/\lambda^5}{\exp(hc/(\lambda k_B T))-1} \tag{2.9}\]を表します。ここで\(B_\nu d\nu = -B_\lambda d\lambda\)の関係があります。恒星における放射に関して現れるプランク関数は(2.9)の定義のように光の強度(intensity)と同じ次元を持った量として定義されます。量子力学などの他の分野ではエネルギー密度orフラックスの次元を持つ量として定義される場合があるので注意してください。恒星大気の外側の密度の非常に小さい層では、LTEからのズレが大きくなります。そのような層で形成されるスペクトル線に対しては、(2.8)式ではなく非局所熱平衡(NLTE)の取り扱いが必要となります。
散乱による発光係数を考えましょう。考えている光の方向の単位ベクトルを\({\bf n}\)とし、\({\bf n}'\)の方向に進んでいた光が、散乱によって\({\bf n}\)の方向に変えられる確率を\(R({\bf n}', {\bf n}) d\Omega' / (4\pi)\)と書くと
のようになります。最後の\(d\Omega' / (4\pi)\)は単位立体角あたりの量に直すための規格化因子です。
散乱では光の振動数は変化しないものと仮定(coherent scattering)をしましょう。恒星大気では多くの場合、近似的に等方的な散乱が起こるので、以下では等方的な散乱\(R({\bf n}', {\bf n}) = 1\)だけを考えましょう。すると上式から
\[\eta^s_\nu = \frac{\sigma_\nu}{4\pi} \int_{4\pi} I({\bf n}') d\Omega' = \sigma_\nu J_\nu \tag{2.11}\]が得られます。ここで
\[J_\nu = \frac{1}{4\pi} \int_{4\pi} I_\nu ({\bf n})d\Omega = \frac{1}{2} \int_{-1}^1 I_\nu (\mu)d\mu \tag{2.12}\]で定義されるこれは平均強度(Mean intensity)と呼ばれます。
このようにLTEとcoherentな等方的散乱を仮定すると、(2.7)式で与えられるtotal emission coefficientは
と書けます。この式を用いると、(2.6)式で与えられる源泉関数は
\[S_\nu = \frac{\kappa_\nu B_\nu + \sigma_\nu J_\nu}{\kappa_\nu + \sigma_\nu} \tag{2.14}\]のように表されます。さらに散乱が無視できるとき(\(\kappa_\nu \gg \sigma_\nu\))、\(S_\nu = B_\nu\)となることを示しています。