リーマンテンソル

リーマンテンソルの計算

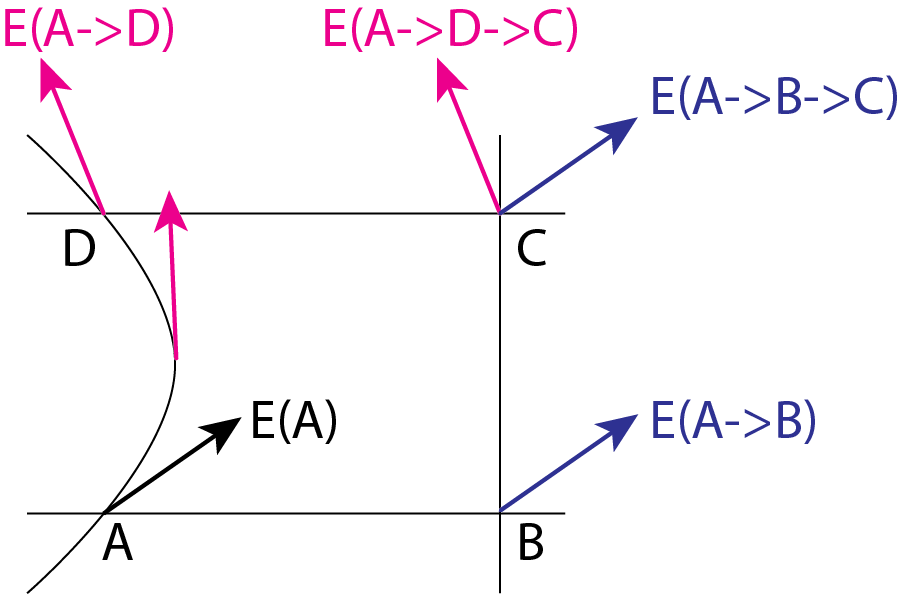
リーマンテンソルの考え方

上図のような曲面でのベクトルの平行移動とその差分を考えましょう。

\[d_1 {\bf E} = \frac{\mathbf{E} (A \rightarrow B) - \mathbf{E}(A)}{\delta x^1}\] \[d_2 {\bf E} = \frac{\mathbf{E} (A \rightarrow D) - \mathbf{E}(A)}{\delta x^2}\]

\(d_1\)は上図の横方向への平行移動をしたときの差分、\(d_2\)は上図の縦方向への平行移動をしたときの差分を表します。これらから、2方向への平行移動を考えましょう。

\[d_2 d_1 {\bf E} = \frac{({\bf E}(A\rightarrow B \rightarrow C) - {\bf E}(A\rightarrow B))-({\bf E}(A\rightarrow B) - {\bf E}(A))}{\delta x^2 \delta x^1}\] \[d_1 d_2 {\bf E} = \frac{({\bf E}(A\rightarrow D \rightarrow C) - {\bf E}(A\rightarrow D))-({\bf E}(A\rightarrow D) - {\bf E}(A))}{\delta x^1 \delta x^2}\]

さらにこの差分をとると

\[d_2 d_1 {\bf E} - d_1 d_2 {\bf E} = \frac{\mathbf{E}(A\rightarrow B \rightarrow C) - \mathbf{E}(A\rightarrow D \rightarrow C)}{\delta x^1 \delta x^2} \neq {\bf 0}\]

となります。これは同じA地点にある同じベクトルを違う経路で曲面上を平行移動すると、違うベクトルになることを意味します。これは空間の曲がり具合を表現していると考えられます。よって交換関係

\[[\nabla_\mu, \nabla_\nu] = \nabla_\mu \nabla_\nu - \nabla_\nu \nabla_\mu\]

をベクトルに作用させたものを

\[[\nabla_\mu, \nabla_\nu] A^\alpha \equiv R^\alpha_{\gamma \mu \nu} A^\gamma \tag{1}\]

の\(R\)をリーマンテンソルと定義します。先ほども記述したとおり、このリーマンテンソルは空間の曲がり具合を表現するものです。
計算を進める前に便利な公式を導出しましょう。反変ベクトルと共変ベクトルの共偏微分より

\[\begin{aligned} \nabla_\mu (A_\alpha B^\beta) &= B^\beta (\nabla_\mu A_\alpha) + A_\alpha (\nabla_\mu B^\beta) = B^\beta (\partial_\mu A_\alpha - A_\gamma \Gamma^\gamma_{\alpha \mu}) + A_\alpha (\partial_\mu B^\beta + B^\gamma \Gamma^\beta_{\mu \gamma}) \\ &= \partial_\mu (A_\alpha B^\beta) - \Gamma^\gamma_{\alpha \mu} (A_\gamma B^\beta) + \Gamma^\beta_{\mu \gamma} (A_\alpha B^\gamma) \end{aligned}\]

これを用いて

\[\begin{aligned} (左辺) &= \nabla_\mu \nabla_\nu A^\alpha -\nabla_\nu \nabla_\mu A^\alpha = \partial_\mu (\nabla_\nu A^\alpha) - \Gamma^\gamma_{\mu \nu} \nabla_\gamma A^\alpha + \Gamma^\alpha_{\mu \gamma} \nabla_\nu A^\gamma - \partial_\nu (\nabla_\mu A^\alpha) + \Gamma^\gamma_{\nu \mu} \nabla_\gamma A^\alpha - \Gamma^\alpha_{\nu \gamma} \nabla_\mu A^\gamma \\ &= \partial_\mu (\partial_\nu A^\alpha + \Gamma^\alpha_{\nu \gamma} A^\gamma) + \Gamma^\alpha_{\mu \gamma} (\partial_\nu A^\gamma + \Gamma^\gamma_{\nu \beta} A^\beta) - \partial_\nu (\partial_\mu A^\alpha + \Gamma^\alpha_{\mu \gamma} A^\gamma) - \Gamma^\alpha_{\nu \gamma} (\partial_\mu A^\gamma + \Gamma^\gamma_{\mu \beta} A^\beta) \\ &= A^\gamma (\partial_\mu \Gamma^\alpha_{\nu \gamma}) + \Gamma^\alpha_{\nu \gamma} (\partial_\mu A^\gamma) + \Gamma^\alpha_{\mu \gamma} (\partial_\nu A^\gamma) + \Gamma^\alpha_{\mu \gamma} \Gamma^\gamma_{\nu \beta} A^\beta - A^\gamma (\partial_\nu \gamma^\alpha_{\mu \gamma}) - \Gamma^\alpha_{\mu \gamma} (\partial_\nu A^\gamma) - \Gamma^\alpha_{\nu \gamma} (\partial_\mu A^\gamma) - \Gamma^\alpha_{\nu \gamma} \Gamma^\gamma_{\mu \beta} A^\beta \\ &= A^\gamma (\partial_\mu \Gamma^\alpha_{\nu \gamma}) + \Gamma^\alpha_{\mu \beta} \Gamma^\beta_{\nu \gamma} A^\gamma - A^\gamma (\partial_\nu \Gamma^\alpha_{\mu \gamma}) - \Gamma^\alpha_{\nu \beta} \Gamma^\beta_{\mu \gamma} A^\gamma \end{aligned}\]

\(A^\gamma\)は任意のベクトルなので、恒等的に

\[R^\alpha_{\gamma \mu \nu} = \partial_\mu \Gamma^\alpha_{\nu \gamma} + \Gamma^\alpha_{\mu \beta} \Gamma^\beta_{\nu \gamma} - \partial_\nu \Gamma^\alpha_{\mu \gamma} – \Gamma^\alpha_{\nu \beta} \Gamma^\beta_{\mu \gamma}\]

が成立します。特に局所慣性系では\(\Gamma = 0\)より

\[\bar{R}^\alpha_{\gamma \mu \nu} = \bar{\partial_\mu} \bar{\Gamma^\alpha_{\nu \gamma}} - \bar{\partial_\nu} \bar{\Gamma}^\alpha_{\mu \gamma}\]

交換関係をスカラー\(\phi\)に作用させると

\[[\nabla_\mu, \nabla_\nu] \phi = 0\]

これはスカラーに向きがなく、曲面の平行移動に関係なく存在する値だからです。これより

\[\begin{aligned} &[\nabla_\mu, \nabla_\nu] (A^\alpha B_\alpha) = ([\nabla_\mu, \nabla_\nu] A^\alpha) B_\alpha + A^\alpha ([\nabla_\mu, \nabla_\nu] B_\alpha) = 0 = R^\alpha_{\gamma \mu \nu} A^\gamma B_\alpha + A^\alpha ([\nabla_\mu, \nabla_\mu] B_\alpha) \\ &\Longrightarrow \ A^\alpha ([\nabla_\mu, \nabla_\nu]B_\alpha) = - R^\gamma_{\alpha \mu \nu} A^\alpha B_\gamma \end{aligned}\]

\(A^\alpha\)は任意のベクトルなので

\[[\nabla_\mu, \nabla_\nu] B_\alpha = - R^\gamma_{\alpha \mu \nu} B_\gamma\]

リーマンテンソルの公式

計量テンソルを用いて添字の上げ下げを行います。

\[R_{\alpha \gamma \mu \nu} = g_{\alpha \sigma} R^\sigma_{\ \gamma \mu \nu}\]

局所慣性系では

\[\begin{aligned} R_{\sigma \gamma \mu \nu} &= \eta_{\alpha \sigma} (\partial_\mu \Gamma^\sigma_{\nu \gamma} -\partial_\nu \Gamma^\sigma_{\mu \gamma}) = \eta_{\alpha \sigma} \frac{1}{2} \partial_\mu (\eta^{\sigma \rho} (\eta_{\rho \nu, \gamma}+ \eta_{\rho \gamma, \nu} - \eta_{\nu \gamma, \rho})) + \eta_{\alpha \sigma} \frac{1}{2} \partial_\nu (\eta^{\sigma \rho} (\eta_{\rho \mu, \gamma} + \eta_{\rho \gamma, \mu}- \eta_{\mu \gamma, \rho})) \\ &= \frac{1}{2} \sigma^\rho_\alpha (\eta_{\rho \nu, \gamma \mu}-\eta_{\nu \gamma, \rho \mu} - \eta_{\rho \mu, \gamma \nu} + \eta_{\mu \gamma, \rho \nu}) = \frac{1}{2} (\eta_{\alpha \nu, \gamma \mu} - \eta_{\nu \gamma, \alpha \mu} - \eta_{\alpha \mu, \gamma \nu} + \eta_{\mu \gamma, \alpha \nu}) \end{aligned}\]

ここで\(\eta_{\rho \nu, \gamma \mu} = \partial_\mu \partial_\gamma \eta_{\rho \nu}\)のような記法を用いました。
これより

\[R_{\mu \nu \alpha \gamma} = \frac{1}{2} (\eta_{\mu \gamma, \nu \alpha} - \eta_{\gamma \nu, \mu \alpha} - \eta_{\mu \alpha, \nu \gamma} + \eta_{\alpha \nu, \mu \gamma}) = R_{\alpha \gamma \mu \nu}\] \[R_{\alpha \gamma \mu \nu} = \frac{1}{2} (\eta_{\gamma \nu, \alpha \mu} - \eta_{\nu \alpha, \gamma \mu} - \eta_{\gamma \mu, \alpha \nu} + \eta_{\mu \alpha, \gamma \nu}) = - R_{\alpha \gamma \nu \mu}\] \[R_{\alpha \gamma \nu \mu} = R_{\nu \mu \alpha \gamma} = - R_{\mu \nu \alpha \gamma} = - R_{\alpha \gamma \mu \nu}\]

が成立します。