1次元ランダムウォークに関する問題
以下の問題は、2023年冬に行われた東京都立大学大学院物理学専攻の大学院入試問題です。 粒子のランダムな運動の簡単なモデルとして知られるランダムウォークについての問題です。 ランダムウォークの諸性質、そして最後には連続極限での方程式を導出します。 有名な問題なので、知っている方も多いことでしょう。 しかし、初めて見る場合には面食らう問題と感じ、今回はこれを解いてみました。
問題
1次元の\(x\)軸上をランダムウォークする粒子について考えましょう。 1ステップの大きさを\(\xi\)、1ステップにかかる時間を\(\tau\)とします。 各ステップにおいて、\(x\)軸正の向きに進む確率を1/2、負の向きに進む確率を1/2とします。 \(t=0\)において、\(x=0\)の位置に粒子がいるものとします。 そして\(t = N\tau\)のとき、\(x = m\xi\)に粒子が存在する確率を\(W(N, m)\)と書くことにします。 ただし、\(N\)は正の整数、\(m\)は整数かつ\(\vert m \vert \leq N\)です。
問1
\(N\)ステップ後に粒子が存在する位置の期待値を、対称性を考慮して求めなさい。
問2
\(N+1\)ステップで\(x = m\xi\)にいる確率\(W(N+1, m)\)を、\(W(N, m-1)\)と\(W(N, m+1)\)を用いて表しなさい。
問3
具体的に\(W(4, 2)\)を計算しなさい。
問4
\(W(N, m)\)を求めなさい。
問5
\(N\)が十分大きな極限を考えましょう。 以下に示すスターリングの公式を用いて、\(\ln W(N, m)\)を\(m/N\)の2次まで展開し、\(W(N, m)\)が\(m/N\)に対する正規分布となることを示しなさい。 ここで、スターリングの公式は
\[\ln n! \simeq n \ln n - n \qquad (n \gg 1) \tag{1}\]のように書かれます。 また、必要であれば以下の公式を用いても構いません。
\[\ln (1+x) \simeq x - \frac{x^2}{2} \tag{2}\]問6
\(\tau, \xi\)が十分小さいとき、問2で導出した式を用いて\(W(N+1, m)-W(N, m)\)を計算し、その連続極限を取ることで、\(t, x\)に関する\(W\)の偏微分方程式を求めなさい。
解答例
問1
たくさんの粒子がこのランダムウォークするような場合を考えましょう。 すると\(N\)回のステップの間に\(+\xi\)方向に進む粒子もあれば、同じく\(-\xi\)方向に進む粒子も存在します。 このランダムウォークでは\(+\xi\)方向に進む確率と\(-\xi\)方向に進む確率がどちらも等しく1/2であるため、同数程度の粒子が正の方向と負の方向に存在しているはずです。 よって問題の対称性から、粒子が存在する位置の期待値は\(\langle x \rangle = 0\)とわかります。
問2
\((m-1) \xi\)にいる粒子が1/2の確率で\(m\xi\)に移動し、\((m+1)\xi\)にいる粒子が1/2の確率で\(m\xi\)に移動してくるので
\[W(N+1, m) = \frac{1}{2} W(N, m-1) + \frac{1}{2} W(N, m+1) \tag{2-1}\]問3
(2-1)式から、実際に\(W(4, 2)\)を計算していきましょう。
\[\begin{align} W(4, 2) &= \frac{1}{2} W(3, 1) + \frac{1}{2} W(3, 3) \notag \\ &= \frac{1}{2} \left\{ \frac{1}{2} W(2, 0) + \frac{1}{2} W(2, 2) \right\} + \frac{1}{2} \left\{ \frac{1}{2} W(2, 2) + \frac{1}{2} W(2, 4) \right\} \notag \\ &= \frac{1}{4} \{ W(2, 0) + 2 W(2, 2) + W(2, 4)\} \notag \\ &= \frac{1}{4} \left\{ \frac{1}{2} W(1, -1) + \frac{1}{2} W(1, 1)\right\} + \frac{1}{2} \left\{ \frac{1}{2} W(1, 1) + \frac{1}{2} W(1, 3) \right\} + \frac{1}{4} \left\{ \frac{1}{2} W(1, 3) + \frac{1}{2} W(1, 5)\right\} \notag \\ &= \frac{1}{8} \{W(1, -1) + 3 W(1, 1) + 3 W(1, 3) + W(1, 5)\} \notag \\ &= \frac{1}{8} \left\{ \frac{1}{2} W(0, -2) + \frac{1}{2} W(0, 0)\right\} + \frac{3}{8} \left\{ \frac{1}{2} W(0, 0) + \frac{1}{2} W(0, 2)\right\} \notag \\ & \qquad \qquad + \frac{3}{8} \left\{ \frac{1}{2} W(0, 2) + \frac{1}{2} W(0, 4)\right\} + \frac{1}{8} \left\{ \frac{1}{2} W(0, 4) + \frac{1}{2} W(0, 6)\right\} \tag{2-2} \end{align}\]ここまでくれば、初期状態より\(W(0, m) = \delta_{m0}\)なので、これを代入すると\(W(4, 2) = 1/4\)と求まります。
このように数式で表現することもできますが、\(N=4\)ステップ程度ならば下図のような図示からも見積もることができます。
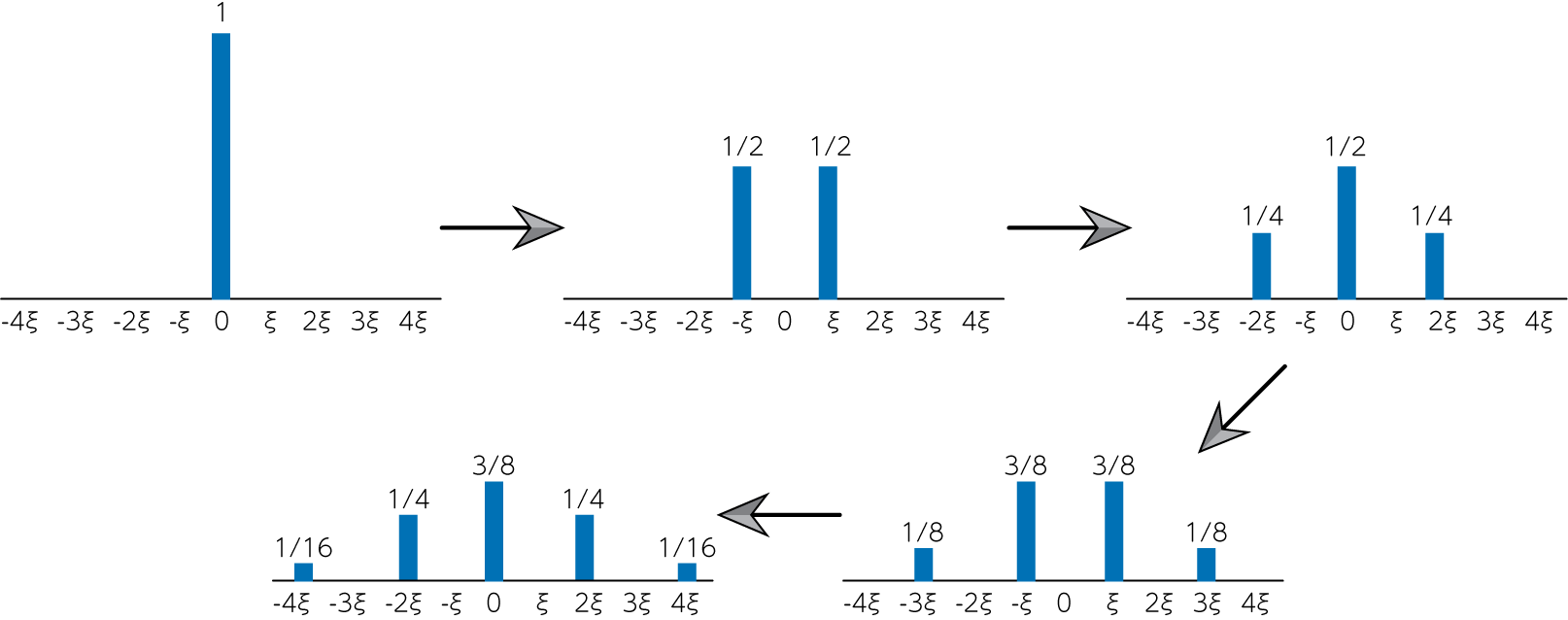
問4
\(N\)ステップの間に、\(+\xi\)方向に進んだ回数を\(n_+\)、\(-\xi\)方向に進んだ回数を\(n_-\)としましょう。 すると
\[n_+ + n_- = N, \qquad n_+ - n_- = m \tag{4-1}\]の関係が成り立ちます。 \(W(N, m)\)は、\(n_+\)回だけ\(+\xi\)方向に進む確率と\(N-n_+(=n_-)\)回だけ\(-\xi\)方向に進む確率、そして\(N\)回のステップから\(n_+\)回だけ\(+\xi\)方向の移動を選ぶ組み合わせの数をかけたものに等しいので
\[W(N, m) = {}_N C_{n_+} \left( \frac{1}{2} \right)^{n_+} \left( \frac{1}{2} \right)^{n_-} = \frac{N!}{n_+! n_-!} \left( \frac{1}{2} \right)^N \tag{4-2}\](4-1)式から
\[n_+ = \frac{N+m}{2}, \qquad n_- = \frac{N-m}{2} \tag{4-4}\]とわかるので
\[W(N, m) = \frac{N!}{\left( \frac{N+m}{2}\right)!\left( \frac{N-m}{2}\right)!} \left( \frac{1}{2}\right)^N \tag{4-3}\]のように、\(N, m\)のみを用いて\(W(N, m)\)を記述することができます。
問5
(4-2)式から計算を行っていきましょう。
\[\ln W(N, m) = \ln N! - \ln n_+! - \ln n_-! - N \ln 2\]\(n_+ \gg 1, n_- \gg 1\)と、スターリングの公式より
\[\begin{align} \ln W(N, m) &= N \ln N - N - (n_+ \ln n_+ - n_+) - (n_- \ln n_- - n_-) - N \ln 2 \notag \\ &\underbrace{=}_{(4-1)} N \ln N - n_+ \ln n_+ - n_- \ln n_- - N \ln 2 \notag \end{align}\]のようになります。 (4-3)式より
\[\ln n_+ = \ln (N+m) - \ln 2 = \ln N + \ln \left( 1 + \frac{m}{N}\right) - \ln 2 \simeq \ln N + \left\{ \frac{m}{N} - \frac{1}{2} \left(\frac{m}{N}\right)^2\right\} - \ln 2\]となります。 途中、テイラー展開(2)式を用いて変形を行いました。 同様に
\[\ln n_- \simeq \ln N + \left\{ -\frac{m}{N} - \frac{1}{2} \left(\frac{m}{N}\right)^2\right\} - \ln 2\]を得ます。 以上より
\[\begin{align} \ln W(N, m) &= -n_+ \left\{ \frac{m}{N} - \frac{1}{2} \left(\frac{m}{N}\right)^2\right\} - n_- \left\{ - \frac{m}{N} - \frac{1}{2} \left(\frac{m}{N}\right)^2\right\} = \frac{m}{N} \underbrace{(-n_+ + n_-)}_{=-m} + \frac{1}{2} \left(\frac{m}{N}\right)^2 (n_+ + n_-) \notag \\ &= - \frac{m^2}{N} + \frac{m^2}{2N} = - \frac{m^2}{2N} \notag \end{align}\]と計算されます。 よって
\[W = e^{-\frac{m^2}{2N}} = e^{-\frac{(m/N)}{2N^2}}\tag{5-1}\]のような正規分布とわかります。
規格化係数が出てこない?スターリングの公式でO(ln n)の項を含めれば出てくるかも?
問6
(2-1)式より
\[\begin{align} W(N+1, m) - W(N, m) &= \frac{1}{2} W(N, m-1) + \frac{1}{2} W(N, m+1) - \frac{1}{2} W(N, m) - \frac{1}{2} W(N, m) \notag \\ &= \frac{1}{2} \{ W(N, m+1) - W(N, m)\} - \frac{1}{2} \{W(N, m) - W(N, m-1)\} \notag \\ &= \frac{\xi}{2} \frac{W(N, m+1) - W(N, m)}{\xi} - \frac{\xi}{2} \frac{W(N, m) - W(N, m-1)}{\xi} \notag \\ &\underbrace{\simeq}_{\xi \rightarrow 0} \frac{\xi}{2} \left( \left. \frac{\partial W}{\partial x} \right|_{x=(m+1/2)\xi} - \left. \frac{\partial W}{\partial x} \right|_{x=(m-1/2)\xi} \right) = \frac{\xi^2}{2} \frac{\partial^2 W}{\partial x^2} \notag \end{align}\]同様に、最左辺も
\[W(N+1, m) - W(N, m) = \tau \frac{W(N+1, m) - W(N, m)}{\tau} \underbrace{\simeq}_{\tau \rightarrow 0} \tau \frac{\partial W}{\partial t}\]のように変形されるので、最終的に
\[\frac{\partial W}{\partial t} = \frac{\xi^2}{2 \tau} \frac{\partial^2 W}{\partial x^2} \tag{6-1}\]のような、拡散方程式となります。