Table of contents
磁気流体での垂直衝撃波
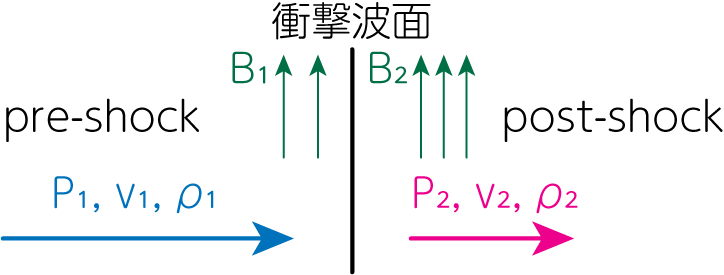
磁場のない流体での垂直衝撃波のときと同様に、衝撃波と同じ速度で運動する座標系で衝撃波を観測しましょう。また衝撃波は定常的に存在し、等速で流体中を伝播していくものとします。 衝撃波面を挟んで上流(pre-shock)側の物理量には1, 下流(post-shock)側の物理量には2の添字をつけて考えます。さらに簡単のため、流体の運動方向は衝撃波面に対して垂直で、磁場の方向は衝撃波面に平行な成分しか存在しないとします。
基礎方程式
連続の式、運動量保存の式、エネルギー保存の式から以下を得ます。
\[\rho_1 v_1 = \rho_2 v_2 \tag{1}\] \[\rho_1 v_1 v_1 + P_1 + \frac{1}{8\pi} B_1^2 = \rho_2 v_2 v_2 + P_2 + \frac{1}{8\pi} B_2^2 \tag{2}\] \[\left( \frac{1}{2} \rho_1 v_1^2 + \rho_1 e_1 + P_1 \right) v_1 + S_1 = \left( \frac{1}{2} \rho_2 v_2^2 + \rho_2 e_2 + P_2 \right) v_2 + S_2 \tag{3}\]ここで
\[e = \frac{1}{\gamma - 1} \frac{P}{\rho}, \quad \mathbf{S} = \frac{c}{4\pi} \mathbf{E} \times \mathbf{B} \tag{4}\]などです。さらにオームの法則から
\[\mathbf{j} = \sigma \left( \mathbf{E} + \mathbf{v} \times \frac{\mathbf{B}}{c} \right) \ \Longrightarrow \ \mathbf{E} = \frac{\mathbf{j}}{\sigma} - \mathbf{v} \times \frac{\mathbf{B}}{c} \underbrace{\simeq}_{\sigma \gg 1} - \mathbf{v} \times \frac{\mathbf{B}}{c} \tag{5}\]です。(3), (4), (5)式より
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1 \right) v_1 - \frac{1}{4\pi} (\mathbf{v}_1 \times \mathbf{B}_1) \times \mathbf{B}_1 = \left( \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma-1} P_2 \right) v_2 - \frac{1}{4\pi} (\mathbf{v}_2 \times \mathbf{B}_2) \times \mathbf{B}_2\]ベクトル解析から
\[\begin{aligned} [(\mathbf{v} \times \mathbf{B}) \times \mathbf{B}]_i &= \epsilon_{ijk} (\mathbf{v} \times \mathbf{B})_j B_k = \epsilon_{ijk} \epsilon_{j\ell m} v_\ell B_m B_k = \epsilon_{jki} \epsilon_{j\ell m} v_\ell B_m B_k \\ &= (\delta_{k\ell} \delta_{i m} - \delta_{k m} \delta_{i \ell}) v_\ell B_m B_k = v_k B_i B_k - v_i B_k B_k = [(\mathbf{B} \cdot \mathbf{v}) \mathbf{B} - B^2 \mathbf{v}]_i = - B^2 v_i \end{aligned}\]最後の等号では、今回の問題設定である\(\mathbf{B} \perp \mathbf{v}\)を用いました。以上より
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1 + \frac{1}{4\pi} B_1^2\right) v_1 = \left( \frac{1}{2} \rho_2 v_2^2 + \frac{\gamma}{\gamma-1} P_2 + \frac{1}{4\pi} B_2^2 \right) v_2 \tag{6}\]最後に誘導方程式を考えます。定常な流れを考えているので
\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) = \mathbf{0}\]この式を下図のような、一辺の長さ\(\ell\)の正方形で面積積分すると

と求まります。
式変形と衝撃波の発生条件
(1), (10)式から
\[\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} = \frac{B_2}{B_1} \equiv X \tag{7}\]さらに
\[\frac{P_2}{P_1} \equiv Y, \quad M_1 = \frac{v_1}{C_{s1}} \tag{8}\]を定義しておきます。すると(2)式より
\[\rho_1 v_1^2 + P_1 + \frac{1}{8\pi} B_1^2 = \rho_1 v_1^2 \frac{1}{X} + P_1 Y + \frac{1}{8\pi} B_1^2 X^2\]のようになります。この両辺を\(P_1\)で割って整理します。このときプラズマベータ\(\beta \equiv \frac{P}{B^2 / 8\pi}\)を用いると
\[\begin{align} &\frac{\rho_1 v_1^1}{P_1} + 1 + \frac{1}{\beta_1} = \frac{\rho_1 v_1^2}{P_1} \frac{1}{X} + Y + \frac{X^2}{\beta_1} \notag \\ &\Longrightarrow \ Y = 1 + \frac{1}{\beta_1} (1-X^2) + \gamma \underbrace{\frac{\rho_1}{\gamma P_1}}_{= C_s^{-2}} v_1^2 \left( 1 - \frac{1}{X}\right) = 1 + \frac{1}{\beta_1} (1-X^2) + \gamma M_1^2 \left( 1 - \frac{1}{X}\right) \tag{9} \end{align}\]のようになります。同様に(6)式から
\[\left( \frac{1}{2} \rho_1 v_1^2 + \frac{\gamma}{\gamma-1} P_1 + \frac{B_1^2}{4\pi} \right) v_1 = \left( \frac{1}{2} \rho_1 v_1^2 \frac{1}{X} + \frac{\gamma}{\gamma-1} P_1 Y + \frac{B_1^2}{4\pi} X^2 \right) \frac{v_1}{X}\]両辺に\(X / \gamma P_1 v_1\)をかけると
\[\left( \frac{1}{2} M_1^2 + \frac{1}{\gamma-1} + \frac{2}{\gamma} \frac{1}{\beta_1}\right) X = \frac{1}{2} M_1^2 \frac{1}{X} + \frac{1}{\gamma-1} Y + \frac{2}{\gamma} \frac{1}{\beta_1} X^2\]となります。左辺に\(Y\)を持ってくると
\[Y = \frac{2(\gamma-1)}{\gamma \beta_1} X(1-X) + X + \frac{\gamma-1}{2} M_1^2 \left( X - \frac{1}{X}\right) \tag{10}\](9), (10)式より
\[\begin{aligned} &- \frac{2(\gamma-1)}{\gamma \beta_1} X^2(X-1) + X^2 + \frac{\gamma-1}{2} M_1^2 \left( X^2 - 1\right) = X - \frac{1}{\beta_1} X(X^2-1) + \gamma M_1^2 \left( X - 1\right) \\ &\Longrightarrow \ (X-1) \left\{ -\frac{2(\gamma-1)}{\gamma \beta_1} X^2 + X + \frac{\gamma-1}{2} M_1^2 (X+1) + \frac{1}{\beta_1} X (X+1) - \gamma M_1^2\right\} = 0 \end{aligned}\]よってこの式を解けば、衝撃波面の前後の物理量の変化がわかります。(7)式より\(X=1\)は\(\rho_1 = \rho_2\)で何も変化がない解です。よって\(\{ \cdots \} = 0\)を解きます。
\[\begin{align} &\frac{2(1 -\gamma)}{\gamma \beta_1} X^2 + X + \frac{\gamma-1}{2} M_1^2 (X+1) + \frac{1}{\beta_1} X (X+1) - \gamma M_1^2 = 0 \notag \\ &\Longrightarrow \ \underbrace{2 (2-\gamma) X^2 + \gamma \beta_1 \left\{ 2 + (\gamma-1) M_1^2 + \frac{2}{\beta_1} \right\} X - \gamma \beta_1 (\gamma+1) M_1^2}_{\equiv f(X)} = 0 \tag{11} \end{align}\]比熱比\(\gamma\)は一般に\(1<\gamma<2\)より、関数\(f(X)\)は下に凸な2次関数とわかります。\(X=1\)のとき\(f(1)<0\)であれば、\(X>1\)で\(f(X)=0\)となる解が存在することになるので
\[f(1) = 2(2-\gamma) + \gamma \beta_1 \left\{ 2+(\gamma-1) M_1^2 + \frac{2}{\beta_1} \right\} - \gamma \beta_1 (\gamma+1) M_1^2 < 0 \ \Longrightarrow \ M_1^2 > 1 + \frac{2}{\gamma \beta_1} \tag{12}\]ここでプラズマベータは
\[\beta = \frac{P}{B^2 / 8\pi} = \frac{\gamma P / \rho}{\frac{\gamma}{2} \frac{B^2}{4 \pi \rho}} = \frac{2}{\gamma} \frac{C_s^2}{v_A^2} \tag{13}\]のようにも書かれます。\(v_A\)はアルヴェーン速度です。これを用いると(12)式は
\[\frac{v_1^2}{C_{s1}^2} > 1 + \frac{v_{A1}^2}{C_{s1}^2} \ \Longrightarrow \ v_1^2 > C_{s1}^2 + v_{A1}^2 \tag{13}\]よってこの場合に衝撃波が起こる条件は、上流側の流体の速度が衝撃波面に乗った系からみて速い磁気音波の位相速度よりも大きくなければならないとわかります。
強い衝撃波極限での圧縮率
強い衝撃波においては\(M_1^2 \gg 1\)です。この条件と(11)式より
\[\gamma \beta_1 (\gamma-1) M_1^2 X - \gamma \beta_1 (\gamma + 1)M_1^2 = 0 \ \Longrightarrow \ X = \frac{\gamma+1}{\gamma-1} = \frac{\rho_2}{\rho_1} = \frac{B_2}{B_1} \tag{14}\]となり、磁場のない流体の垂直衝撃波と同様の結果を得ます。
弱い磁場極限での圧縮率
弱い磁場極限では\(\beta_1 \rightarrow \infty\)です。この条件と(11)式より
\[\gamma \beta_1 \{2+(\gamma-1) M_1^2\} X - \gamma \beta_1 (\gamma+1) M_1^2 = 0 \ \Longrightarrow \ X = \frac{(\gamma +1) M_1^2}{2 + (\gamma-1)M_1^2} \tag{15}\]となり、やはり磁場のない流体の垂直衝撃波と同じ結果となります。
強い磁場極限での圧縮率
今度は強い磁場極限、すなわち\(\beta_1 \rightarrow 0\)の場合を見てみましょう。この条件と(11)式より
\[\begin{align} & 2(2-\gamma) X^2 + 2 \gamma X - \gamma \beta_1 (\gamma+1)M_1^2 = 0 \notag \\ & \Longrightarrow \ X = \frac{-2\gamma \pm \sqrt{4\gamma^2 + 8\gamma \beta_1 (2-\gamma)(\gamma+1)M_1^2}}{4(2-\gamma)} \simeq \frac{\beta_1 (\gamma+1) M_1^2}{2} \tag{16} \end{align}\]となります。強磁場は衝撃波での圧縮率を下げる働きがあることがわかります。これは圧縮に伴う磁気圧の増加が、衝撃波での圧縮を妨げるためです。
等温衝撃波の場合
衝撃波の前後で等温度が保たれる場合、エネルギー保存の式が簡単になります。質量保存、運動量保存、誘導方程式からそれぞれ
\[\rho_1 v_1 = \rho_2 v_2\] \[\rho_1 v_1 v_1 + P_1 + \frac{1}{8\pi} B_1^2 = \rho_2 v_2 v_2 + P_2 + \frac{1}{8\pi} B_2^2\] \[v_1 B_1 = v_2 B_2\]となります。そして等温度条件から
\[\frac{P_1}{\rho_1} = \frac{P_2}{\rho_2} = \frac{k_B}{\mu m_p} T = C_s^2\]です。先程と同様に、圧縮率を
\[\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} = \frac{B_2}{B_1} = x\]とおいて、運動量保存式を解きます。
\[v_1^2 + C_s^2 + \frac{B_1^2}{8\pi \rho_1} = \frac{\rho_2}{\rho_1} \frac{v_2^2}{v_1^2} v_1^2 + C_s^2 \frac{\rho_2}{\rho_1} + \frac{B_1^2}{8\pi \rho_1} \frac{B_2^2}{B_1^2} \ \Longrightarrow \ \left( 1-\frac{1}{x} \right) v_1^2 + (1-x) C_s^2 + (1-x^2) \frac{B_1^2}{8\pi \rho_1} = 0\]両辺を\(C_s^2\)で割り、マッハ数とプラズマベータを用いて式を整理すると
\[(x-1) \left\{ \frac{1}{x} M_1^2 -1 - (1+x) \frac{1}{\beta_1} \right\} = 0\]\(x=1\)は衝撃波としての解ではないため、\(\{\cdots\}=0\)の解を求めましょう。
\[\beta_1^{-1} x^2 + (\beta_1^{-1} + 1) x - M_1^2 = 0 \ \Longrightarrow \ x = \frac{-(1+\beta_1) \pm \beta_1 \sqrt{\beta_1^{-2} + (2 + 4M_1^2) \beta_1^{-1} + 1}}{2}\]圧縮率は必ず正の値を取るので
\[x = \frac{-(1+\beta_1) + \beta_1 \sqrt{\beta_1^{-2} + (2 + 4M_1^2) \beta_1^{-1} + 1}}{2}\]が求めたかった圧縮率となります。弱い磁場の極限、すなわち\(\beta_1^{-1} \rightarrow 0\)では
\[x \simeq \frac{-(1+\beta_1) + \beta_1 \{1 + (1+2M_1^2) \beta_1^{-1}\}}{2} = M_1^2 \tag{17}\]となり、磁場のない流体の等温垂直衝撃波の場合と一致します。
参考文献
[1] Priest, “Solar Magnetohydrodynamics”