衝撃波
ここでは磁場を考えない、流体衝撃波(hydrodynamical shock)について考えます。
垂直・断熱衝撃波
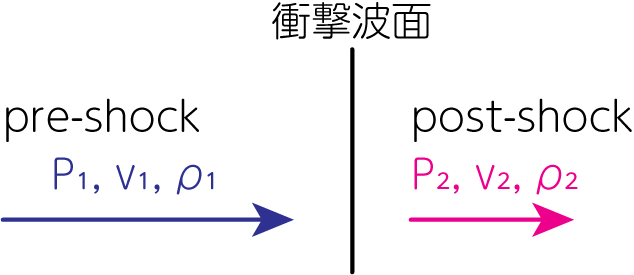
衝撃波面と同じ速度で運動する系で衝撃波を観測してみましょう。簡単のため、衝撃波面は定常・等速度で伝播していくものとし、さらに流体は衝撃波面に対して垂直な方向した運動していないとします。また流体の速度は非相対論的とします。
以降、衝撃波面を挟んで上流側(pre-shock)の物理量には1、下流側(post-shock)の物理量には2の添字をつけて式変形を考えていきます。
質量保存(連続の式)より、衝撃波面を挟んで、その前後では
運動量保存式より
\[\rho_1 v_1 v_1 + P_1 = \rho_2 v_2 v_2 + P_2 \tag{2}\]エネルギー保存式より
\[\left( \frac{1}{2} v^2_1 + e_1 + \frac{P_1}{\rho_1} \right) \rho_1 v_1 = \left( \frac{1}{2} v^2_2 + e_2 + \frac{P_2}{\rho_2} \right) \rho_2 v_2 \tag{3}\]です。ここで\(e\)は単位体積あたりの内部エネルギー\(e = \frac{P}{(\gamma-1) \rho}\)です。以下では
\[\frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} \equiv x, \quad \frac{P_2}{P_1} \equiv y \tag{4}\]のように変数変換をして、式変形を進めましょう。この\(x\)を圧縮率と呼びます。(2)式より
\[\rho_1 v_1^2 + P_1 = \rho_1 v_1^2 \frac{\rho_2}{\rho_1} \frac{v_2^2}{v_1^2} P_1 \frac{P_2}{P_1} \underbrace{=}_{(4)} \frac{\rho v_1^2}{x} + P_1 y\]ここでさらに
\[C_s^2 = \frac{\gamma P_1}{\rho_1}, \quad M \equiv \frac{v}{C_s}\]のように音速とMach数を導入すると
\[\rho_1 v_1^2 + \frac{\rho_1 C_{s1}^2}{\gamma} = \frac{\rho_1 v_1^2}{x} + \frac{\rho_1 C_{s1}^2}{\gamma} y \ \underbrace{\Longrightarrow}_{\times \rho^{-1} C_{s1}^{-2}} \ M_1^2 + \frac{1}{\gamma} = \frac{M_1^2}{x} + \frac{y}{\gamma} \ \Longrightarrow \ y = 1 + \gamma M_1^2 \left( 1-\frac{1}{x}\right) \tag{5}\](1), (3)式より
\[\begin{aligned} &\frac{1}{2} v_1^2 + \frac{\gamma}{\gamma-1} \underbrace{\frac{P_1}{\rho_1}}_{= C_{s1}^2/\gamma} = \frac{1}{2} v_2^2 + \frac{\gamma}{\gamma-1} \frac{P_2}{\rho_2} = \frac{1}{2} v_1^2 \frac{v_2^2}{v_1^2} + \frac{\gamma}{\gamma-1} \frac{P_1}{\rho_1} \frac{P_2}{P_1} \frac{\rho_1}{\rho_2} = \frac{1}{2} \frac{v_1^2}{x^2} + \frac{C_{s1}^2}{\gamma-1} \frac{y}{x} \\ &\Longrightarrow \ \frac{\gamma-1}{2} M_1^2 \left( 1- \frac{1}{x^2} \right) + \left( 1-\frac{y}{x}\right) = 0 \end{aligned}\]この両辺に\(x^2\)をかけて、さらに(5)式を用いると
\[\frac{\gamma-1}{2} M_1^2 (x^2-1) + \left\{ x^2 - x - \gamma M_1^2 (x-1) \right\} = 0 \ \Longrightarrow \ (x-1) \left\{ \frac{\gamma-1}{2} M_1^2 (x+1) + x - \gamma M_1^2 \right\} = 0\]よってこの式には
\[x-1 = 0, \quad \frac{\gamma-1}{2} M_1^2 (x+1) + x - \gamma M_1^2 = 0\]の2つの解があることがわかります。最初の\(x=1\)の解は\(\rho_1 = \rho_2, v_1 = v2, P_1 = P_2\)で、衝撃波面を挟んで何も起こっていないような解なので、この解に意味はありません。よって2つ目の解について調べましょう。すると(5)式より
\[x = \frac{\rho_2}{\rho_1} = \frac{v_1}{v_2} = \frac{(\gamma+1)M_1^2}{(\gamma-1)M_1^2 + 2}, \quad y = \frac{P_2}{P_1} = 1 + \gamma M_1^2 \left( 1 - \frac{(\gamma-1)M_1^2 + 2}{(\gamma+1)M_1^2}\right) = \frac{2\gamma M_1^2 - \gamma + 1}{\gamma + 1} \tag{6}\]この衝撃波面前後での物理量のジャンプ条件をRankine-Hugoniot(ランキン・ユゴニオ)の式と呼びます。もし上流側の流体の速度がとても大きい場合、(6)式で\(M_1 \rightarrow \infty\)の極限をとると
\[x \rightarrow \frac{\gamma + 1}{\gamma -1}, \quad y \rightarrow \frac{2\gamma}{\gamma+1} M_1^2 \tag{7}\]のようになります。どんなに流体の速度が大きく強い衝撃波であったとしてもしても、断熱の物理条件では有限の圧縮率になることがわかります。特に理想気体\(\gamma = 5/3\)のときは\(x = 4\)です。断熱の場合、衝撃波で強く圧縮しようとしても圧力上昇からそこまで圧縮することができず、密度圧縮率が有限の値になります。
衝撃波の発生条件
ガスのエントロピー
衝撃波の前後で変化が起こる量としてエントロピーがあります。よってここではガスの単位体積あたりのエントロピーの導出から行いましょう。エネルギー保存則を求める過程で出現した内部エネルギーが満たす式より
\[\rho \frac{De}{Dt} + \rho P \frac{D}{Dt} \left( \frac{1}{\rho} \right) = -\mathcal{L}\]これと内部エネルギーが\(e = \frac{P}{(\gamma-1) \rho}\)と書かれることより
\[\begin{aligned} \frac{\rho}{\gamma-1} \frac{D}{Dt} \left( \frac{P}{\rho}\right) - \frac{P}{\rho} \frac{D\rho}{Dt} &= \frac{1}{\gamma-1} \frac{DP}{Dt} - \frac{\gamma}{\gamma-1} \frac{P}{\rho} \frac{D\rho}{Dt} = \frac{\rho^\gamma}{\gamma-1} \left( \rho^{-\gamma} \frac{DP}{Dt} - \gamma \rho^{-\gamma-1} \frac{D\rho}{Dt}\right) \\ &= \frac{\rho^\gamma}{\gamma-1} \frac{D}{Dt} \left( \frac{P}{\rho^\gamma}\right) = - \mathcal{L} \end{aligned}\]のように整理されます。さらにこの式は定積熱容量を用いると
\[\rho^\gamma \frac{\mu}{k_B} C_V \frac{D}{Dt} \left( \frac{P}{\rho^\gamma} \right) = \rho^\gamma \frac{\rho T}{P} C_V \frac{D}{Dt} \left( \frac{P}{\rho^\gamma} \right) = \rho C_V T \frac{D}{Dt} \left( \log \frac{P}{\rho^\gamma} \right) = -\mathcal{L}\]のようになります。そもそものエントロピーが満たす式
\[\rho T \frac{Ds}{Dt} = - \mathcal{L}\]との比較から、エントロピーが
\[s = C_V \log \frac{P}{\rho^\gamma} \tag{8}\]のように表記できるとわかります。
衝撃波でのエントロピー変化と衝撃波発生条件
衝撃波前後のエントロピーの差をとると
\[s_2 - s_1 = C_V \log \left\{ \frac{P_2}{P_1} \left( \frac{\rho_1}{\rho_2} \right)^\gamma \right\} = C_V \log \frac{P_2}{P_1} - \gamma C_V \log \frac{\rho_2}{\rho_1}\]両辺を\(M_1\)で微分します。下流の物理量が上流の流体の速度に依存しているのに対して、上流の物理量は特に上流の流体の速度に依存していないと考えると\(P_1, \rho_1, s_1\)はこの微分に関して定数と考えることができます。よって
\[\frac{ds_2}{dM_1} = C_V \frac{d}{dM_1} \log P_2 - \gamma C_V \frac{d}{dM_1} \log \rho_2 = \frac{C_V}{P_2} \frac{dP_2}{dM_1} - \frac{\gamma C_V}{\rho_2} \frac{d\rho_2}{dM_1}\]また(6)式より
\[\frac{dP_2}{dM_1} = \frac{4\gamma}{\gamma+1} M_1 P_1\] \[\frac{d\rho_2}{dM_1} = \frac{4(\gamma+1) M_1}{\{ 2+(\gamma-1) M_1^2\}^2} \rho_1\]以上より
\[\begin{align} \frac{ds_2}{dM_1} &= C_V \frac{P_1}{P_2} \frac{4\gamma}{\gamma+1} M_1 - \gamma C_V \frac{\rho_1}{\rho_2} \frac{4(\gamma+1) M_1}{\{ 2+(\gamma-1) M_1^2\}^2} \notag \\ &\underbrace{=}_{(6)} C_V \frac{4\gamma}{2\gamma M_1^2 - \gamma + 1} M_1 - \frac{\gamma C_V}{M_1} \frac{4}{2+(\gamma-1) M_1^2} \notag \\ &= 4\gamma C_V \frac{(\gamma-1) (M_1^2-1)^2}{M_1 (2\gamma M_1^2-\gamma+1)(2+(\gamma-1)M_1^2)} \tag{9} \end{align}\](6)式の\(P_2/ P_1>0\)より\(2\gamma M_1^2-\gamma+1>0\)であることが保証されます。比熱比は一般に\(\gamma>1\)なので、(9)式の最右辺は0より大きく、\(ds_2/dM_1 > 0\)となります。\(M_1 = 1\)のとき(9)式から\(ds_2/dM_1=0\)となることからもわかるように、上流側と下流側で物理量が全て同じとなり\(s_1 = s_2\)となります。よって衝撃波が発生している\(M_1 > 1\)のときには常に\(s_2 > s_1\)が成立します。逆を言えば、\(M_1>1\)が衝撃波の発生条件と考えることができます。
下流側の速度
次は下流側の流体の速度について考えましょう。
\[M_2^2 = \frac{v_2^2}{C_{s2}} = \frac{\rho_1}{\gamma P_1} \frac{\rho_2}{\rho_1} \frac{P_1}{P_2} \frac{v_2^2}{v_1^2} v_1^2 \underbrace{=}_{(6)} \frac{v_1^2}{C_{s1}^2} \frac{1}{xy} = M_1^2 \frac{2 + (\gamma-1) M_1^2}{(\gamma+1) M_1^2} \frac{\gamma+1}{2\gamma M_1^2-\gamma+1}\]これより
\[M_2^2 -1 = -\frac{M_1^2-1}{\frac{2\gamma}{\gamma+1} (M_1^2-1) + 1} \tag{10}\]これと先程の衝撃波発生条件\(M_1>1\)と合わせると\(M_2^2<1\)であり、下流側は必ず亜音速となることがわかります。
垂直・等温衝撃波
実際の星間空間では衝撃波で加熱された星間ガスは放射を出し、エネルギーを失って冷却されます。冷却時間が着目している物理現象の時間スケールよりも十分に短い場合には、一度衝撃波により加熱されたとしてもすぐに冷却過程が起こります。このような場合、結果として衝撃波の前後で温度の変化が起こらないと見なすことができます。これを等温衝撃波(isothermal shock)と呼びます。以下では等温衝撃波でのジャンプ条件を求めてみましょう。
質量保存・運動量保存・エネルギー保存((1), (2), (3)式)に変化はなく、唯一変わるのは音速の式です。等温条件から圧力と音速は
のようになります。これは先程までの断熱衝撃波で考えた音速において\(\gamma=1\)とした場合と同じです。よって(6)式から、等温衝撃波では
\[x = y = M_1^2 \tag{11}\]となります。断熱の場合と違い、流体の速度が大きくなればなるほど圧縮率が大きくなります。これは先述の通り、衝撃波で圧縮されても温度が上がらないことから圧力上昇が鈍くなり、いくらでも圧縮できることを表しています。