Table of contents
固有体積要素
固有距離を用いて、膨張する宇宙の固有体積要素を求めてみましょう。
固有体積要素の導出
図を用いて3次元の体積要素を考えてみましょう。
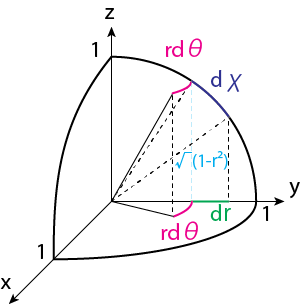
より、固有体積要素は
\[dV(z) = a^3 (z) d\chi r^2 \underbrace{\sin \theta d\theta d\varphi}_{=d\Omega} = \frac{1}{(1+z)^3} r^2 (z) d\chi(z) d\Omega\]固有距離より
\[d\chi = -\frac{c}{H_0} \frac{dz}{E(z)} \tag{1}\]です。
\[dV(z) = - \frac{c}{H_0 (1+z)^3} \frac{r^2 (z)}{E(z)} d\Omega dz\](1)式より\(dz > 0\)のときに\(d\chi <0\)のため、\(dV<0\)です。しかし遠方である(\(dz > 0\))に行くほど\(d\chi < 0\)というのは天文学的な考え方・直感に反します。よって以下では
\[dV(z) = \frac{c}{H_0 (1+z)^3} \frac{r^2 (z)}{E(z)} d\Omega dz\]のように計算します。
共動座標における数密度の導出
固有体積要素\(dV(z)\)あたりに存在する銀河の数を\(dN(z)\)とすると
\[dN(z) = n(z) dV = n(z) \frac{c}{H_0 (1+z)^3} \frac{r^2 (z)}{E(z)} d\Omega dz\]ここで\(n(z)\)は固有数密度です。
\[\therefore \ \frac{dN(z)}{dz d\Omega} = \frac{n(z)}{(1+z)^3} \frac{c}{H_0} \frac{r^2(z)}{E(z)}\]よって\(n_c (z) \equiv n(z) /(1+z)^3\)を共動座標における数密度と定義します。
例: 天体の個数密度が進化しない場合
\[n_0 a_0^3 = n(z) a^3 \ \Longrightarrow \ n_0 = \frac{n(z)}{(1+z)^3} = {\rm Const}\]という関係が成り立ちます。
例: 天体の進化によって個数密度が進化する場合
\[n_c (z) = n_0 f(z)\]のようにして、\(f(z)\)を天体の進化による因子にします。