Table of contents
ランダムスピン系
今度は相互作用係数が\(J = J_{ij}\)のように、一様ではなく考えるペアによって異なる場合を考えましょう。
\[E({\bf{x}}) = - \sum_{\langle i, j \rangle} J_{ij} x_i x_j - h \sum_{i=1}^N x_i \tag{2.1}\]以降、次のような記号を用いて図示を行います。
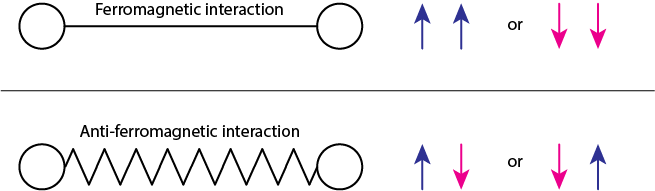
もし隣り合うスピンが強磁性(ferromagnetic)相互作用をしている場合は棒線(solid line)、反強磁性(anti-ferromagnetic)相互作用をしている場合は波線(wave line)で表現します。
フラストレーションが起こる系 (frustration)
次のような3つのスピンを考えましょう。2つの相互作用は強磁性、1つは反強磁性であるとします。この系の基底状態はどのようになるでしょうか。

1番のスピンから時計回りに考えましょう。1番と2番は強磁性相互作用なので、スピンが平行になります。次に2番と3版は反強磁性相互作用なので、3版のスピンは逆向きになります。しかし、3番と1番は強磁性相互作用をしているので、矛盾が生じます。
同様に1番のスピンから反時計回りに考えると、今度は1番と2番のスピンの向きに矛盾が生じます。
このように、基底状態が自明ではなく縮退しており、求めるのが難しいような系をフラストレーションしていると呼びます。このような理由から、ランダムスピン系は複雑です。これは強磁性体と反強磁性体を混ぜて作られた合金や不純物が存在するような物質で起こります。またその物質の作り方などにも依存します。
\(J_{ij}\)のランダム性を仮定
ここで\(J_ij\)が何かしらの確率分布に従って存在しているという、理論的な仮定をすることで、簡単に(解析的に)解くことができるようになります。以下に代表的な確率分布を示します。
\[P(J_{ij}) = \sqrt{\frac{N}{2\pi J^2}} \exp \left( -\frac{N}{2J^2} J_{ij}^2\right) \tag{2.2}\] \[P(J_{ij}) = p \delta(J_{ij}-J) + (1-p) \delta(J_{ij} + J) \tag{2.3}\]特に(2.3)式で表されるランダムスピン系をプラスマイナスJイジングモデルと呼びます。
Sherrington-Kirkpatrick model (SK model)
ここでは以下のようなエネルギーのモデルを考えます。
\[E({\bf{x}}) = - \sum_{i < j} J_{ij} x_i x_j \tag{2.4}\]ここから、分配関数は
\[Z = \sum_{\bf{x}} \exp \left( \beta \sum_{i < j} J_{ij} x_i x_j \right) \tag{2.5}\]のように書かれます。
Self-averaging property (自己平均性)
\(\sum_{i\neq j} x_i x_j = \left( \sum_i x_i \right)^2 - \sum_i x_i^2\)のテクニックを使いたいところですが、(2.5)式の和においては\(J_{ij}\)も添字\(i, j\)に依存しているため、これが使えません。
最終的な目標は1自由度あたりの自由エネルギー\(-\beta f = \frac{1}{N} \log Z\)を求めることでした。そしてここでは\(N \rightarrow \infty\)の系を考えているので
のように\(J_{ij}\)について平均を取ったものと等価です。ここでは\(J_{ij}\)がガウス分布(2.2)式の分布に従うとします。
Replica method (レプリカ法)
上述の計算を行うために、以下の対数の公式を用います。
\[\left[ \log Z \right] = \lim_{n \rightarrow 0} \frac{[Z^n ]- 1}{n} \tag{2.7}\]対数関数をべき乗関数に置き換えることによって、平均が分配関数に直接かかります。これにより計算ができるようになります。
ここで\(n \in \mathbb{R}\)ですが、この計算を進めるために\(n \in \mathbb{N}\)のようにします。すると\(Z^1\)は系が1つ、\(Z^2\)は同じ系が2つ、\(Z^3\)は同じ系が3つ、のように\(n\)は系のコピーの数(レプリカの数)と考えることができます。\(n\)を自然数の場合を考えてから、それを\(n\)が実数の場合に解析接続します(自然数を感じさせない形にしてから実数に拡張を行います)。
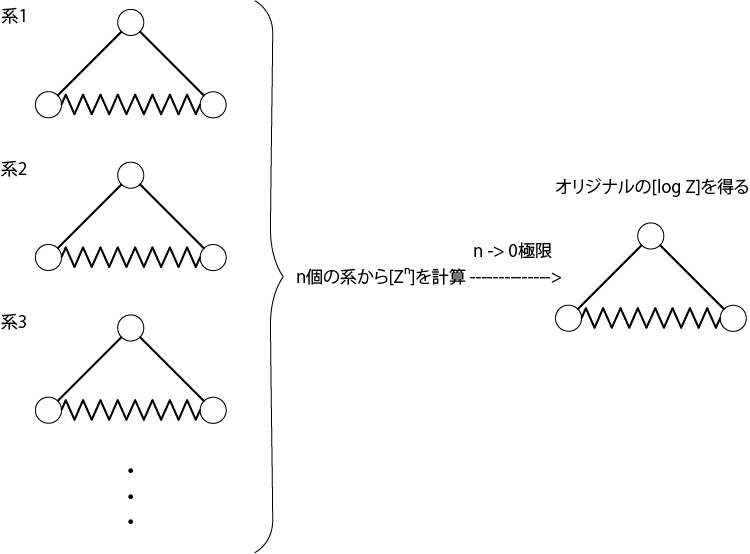
上図の左のように系のレプリカが\(n\)個ある場合の平均を計算し、\(n \rightarrow 0\)とすれば、最終的に上図の右のようにオリジナルの系の\(\log Z\)を計算できたことになります。これがレプリカ法です。
それでは計算を行っていきましょう。
\(e\)の肩だけ取り出して整理すると
\[-\frac{N}{2J^2} \left( J_{ij} - \sum_{a=1}^n \frac{\beta J^2}{N} x_i^a x_j^a \right)^2 + \frac{\beta^2 J^2}{2N} \left( \sum_{a=1}^n x_i^a x_j^a \right)^2\]となるので、\(J_{ij}\)についてガウス積分を行うと
\[[\cdots]_{J_{ij}} \propto \exp \left( \frac{\beta^2 J^2}{2N} \left( \sum_{a=1}^n x_i^a x_j^a \right)^2\right)\]よって
\[\begin{align} [Z^n] &= \sum_{\bf{x}} \prod_{i < j} \exp \left( \frac{\beta^2 J^2}{2N} \left( \sum_{a=1}^n x_i^a x_j^a \right)\right) = \sum_{\bf{x}} \prod_{i < j} \exp \left( \frac{\beta^2 J^2}{2N} \sum_{a, b} x_i^a x_j^a x_i^b x_j^b \right) \notag \\ &= \sum_{\bf{x}} \prod_{i < j} \exp \left( \frac{\beta^2 J^2}{2N} \sum_{a, b} x_i^a x_i^b x_j^a x_j^b \right) = \sum_{\bf{x}} \exp \left( \frac{\beta^2 J^2}{2N} \sum_{a, b} \sum_{i < j} x_i^a x_i^b x_j^a x_j^b \right) \tag{2.9} \end{align}\]\(\sum_{i < j} x_i^a x_i^b x_j^a x_j^b = \frac{1}{2} \left[ \left( \sum_i x_i^a x_i^b \right)^2 - (x_i^a x_i^b)^2 \right]\)となります。\(i \neq j\)の場合と異なり、要素の数が少ないことに注意が必要です。
これより
\[[Z^n] = \sum_{\bf{x}} \exp \left( \frac{\beta^2 J^2}{4N} \sum_{a, b} \left( \sum_{i=1}^N x_i^a x_i^b \right)^2 -\frac{\beta^2 J^2}{4N} N\right) \tag{2.10}\]\(e\)の肩の第一項は\(\mathcal{O}(N)\)ですが、第二項は\(\mathcal{O}(1)\)なので、第二項は無視できます。よって
\[[Z^n] = \sum_{\bf{x}} \exp \left( \frac{N\beta^2 J^2}{4} \sum_{a, b} \left( \frac{1}{N} \sum_{i=1}^N x_i^a x_i^b \right)^2 \right) \tag{2.11}\]ここで新しい秩序パラメータ
\[q^{ab} \equiv \frac{1}{N} \sum_{i=1}^N x_i^a x_i^b \tag{2.11}\]を導入します。同じ位置ですがレプリカが異なるものの積(内積のようなもの、オーバーラップを取ったもの)\(x_i^a x_i^b\)を、全てにおいて平均したようなものを定義します。これをスピングラス(spin glass)オーダーパラメータと呼びます。この系では磁化\(m\)のかわりに、これが同じ働きをします。

これは同じ系を複数回実験して実現された結果1, 結果2, …結果\(n\)において、ある指定された場所のオーバーラップの平均、と見ることができます。もし系が高温で無秩序な状態なら、実験を繰り返すごとにスピンの向きはバラバラとなります。よって\(q^{ab} \sim 0\)です。もし系が低温状態ならば、スピンが上向き・下向きのどちらかに固まります。今、\(J_{ij}\)が強磁性・反磁性相互作用を持っているので、ある1回の実験結果における空間分布は無秩序です。しかし、実験を何度も繰り返すと「ある場所のスピンは上向きの傾向にある」「違う場所ではスピンは下向きの傾向にある」という情報がわかります。よって、この量からはスピンの凍結度合いを測定することができます。
計算を進めるために、以下のテクニックを使いましょう。
\[\int dq^{ab} \ f(q^{ab}) \delta \left( Nq^{ab} - \sum_{i=1}^N x_i^a x_i^b \right) = \frac{1}{N} f\left( \frac{1}{N} \sum_{i=1}^{N} x_i^a x_i^b \right) \tag{2.12}\]オンライン動画のTechnique 2の式と形が違うの注意が必要です。
すると
\[[Z^n] = N \sum_{\bf{x}} \int dQ \ \exp \left( \frac{N \beta^2 J^2}{4} \sum_{a, b} \left( q^{ab} \right)^2\right) \prod_{a, b} \delta \left( N q^{ab} - \sum_{i=1}^N x_i^a x_i^b \right) \tag{2.13}\]ここで\(Q\)は\(q^{ab}\)を全ての\(a, b\)に対してまとめたもので、以下のような\(n \times n\)の行列です。
\[Q = \left( q^{ab} \right)\]イジングモデルからの類推で、最初の\(\exp (\cdots)\)の部分はエネルギーを表す項、そのあとの\(\prod \delta (\cdots)\)の部分はエントロピーを表す項と考えることができます。よって
\[[Z^n] \simeq \int dQ \ \exp (-N \beta e(Q) + NS(Q)) \tag{2.14}\]となります。\(N \rightarrow \infty\)を考えているので、イジングモデルのときと同様に鞍点法を用います。すると\(\int dQ\)部分は\(\exp (-N \beta e(Q^\ast) + NS(Q^\ast))\)となります。これに比べて、前に付いていた\(N = e^{\log N}\)は無視できるとしました。
エントロピーの計算
\[S(Q) = \frac{1}{N} \log \sum_{\bf{x}} \prod_{a,b} \delta \left( N q^{ab} - \sum_{i=1}^N x_i^a x_i^b \right) \tag{2.15}\]デルタ関数をフーリエ積分表示しましょう。
\[\delta \left( N q^{ab} - \sum_{i=1}^N x_i^a x_i^b \right) = \int d\tilde{q}^{ab} \ \exp \left( -\frac{\tilde{q}^{ab}}{2} \left( N q^{ab} - \sum_{i~1}^N x_i^a x_i^b \right)\right) \tag{2.16}\]すると
\[S(Q) = \frac{1}{N} \log \int \tilde{dQ} \ \sum_{\bf{x}} \exp \left( -\sum_{a, b} \frac{N q^{ab} \tilde{q}^{ab}}{2} + \frac{1}{2} \sum_{a, b} \tilde{q}^{ab} \sum_{i=1}^N x_i^a x_i^b \right) \tag{2.17}\]このままでは計算が難しいので、次に示す仮定を用います。
レプリカ対称性 (replica symmetry)
レプリカの添字\(a, b\)に対する対称性を仮定します。
\[Q = \left( \begin{array}{cccc} 1 & q & \cdots & q \\ q & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & q\\ q & \cdots & q& 1 \end{array} \right), \ \tilde{Q} = \left( \begin{array}{cccc} \tilde{Q} & \tilde{q} & \cdots & \tilde{q} \\ \tilde{q} & \tilde{Q} & \ddots & \vdots \\ \vdots & \ddots & \ddots & \tilde{q} \\ \tilde{q} & \cdots & \tilde{q} & \tilde{Q} \end{array} \right) \tag{2.18}\]これは単純に考えて、全てのレプリカは同等なので添字依存性を考える必要はないとの考え方からくる自然なものです。
\[\begin{align} \frac{1}{2} \sum_{a,b} \tilde{q}^{ab} \sum_{i=1}^N x_i^a x_i^b &= \frac{1}{2} \tilde{Q} \sum_{a} \sum_{i=1}^N \underbrace{x_i^a x_i^a}_{=1} + \frac{1}{2} \tilde{q} \sum_{a\neq b} \sum_{i=1}^N x_i^a x_i^b \notag \\ &= \frac{1}{2} nN\tilde{Q} + \frac{1}{2} \tilde{q} \sum_{i=1}^N \left\{ \left( \sum_{a=1}^n x_i^a \right)^2 - \sum_{a=1}^n (x_i^a)^2 \right\} \tag{2.19} \end{align}\]\(\sum_{a, b} q^{ab} \tilde{q}^{ab} = {\rm Tr}[Q \tilde{Q}]\)のようにトレースを用いて表記する教科書もあります。 トレースは同じ要素番号同士のものを掛け合わせて、足し合わせたものです(Trで書いている人はレプリカ法マスターか冷たい人、Trで書いていない人は初心者か優しい人?)。 ここで、元々計算したかったものは\(S(Q) = \sum_{\bf{x}} \exp (\cdot (\sum x_i^a)^2)\)という形なので、このままでは計算できません。ここで以下のHubbard-Stratonovich 変換を用いましょう。
\[\exp \left\{ \frac{1}{2} \tilde{q} \left( \sum_a x_i^a \right)^2\right\} = \int \frac{dz}{\sqrt{2\pi}} \exp \left( -\frac{1}{2} z^2 \right) \exp \left( z \sqrt{\tilde{q}} \sum_a x_i^a \right) \tag{2.20}\]ガウス分布部分は頻繁に出てくるので、これを簡略して\(D_z \equiv \frac{dz}{\sqrt{2\pi}} \exp \left( -\frac{1}{2} z^2 \right)\)と表記しましょう。すると
\[(2.19) \ \Longrightarrow \ \int D_z \exp \left\{ \frac{1}{2} n N (\tilde{Q}-\tilde{q}) + \sqrt{\tilde{q}} z \sum_{i=1}^N \sum_{a=1}^n x_i^a \right\}\](2.17)式から、この部分で\(\sum_{\bf{x}}\)を実行すると
\[\int D_z \exp \left\{ \frac{1}{2} n N (\tilde{Q}-\tilde{q}) \right\} (2 \cosh \sqrt{\tilde{q}}z )^{nN} \tag{2.21}\]となります。\(z\)で積分している部分だけ注目しましょう。
\[\begin{align} \int D_z \exp \left\{ nN \log (2 \cosh \sqrt{\tilde{q}} z) \right\} &\underbrace{\simeq}_{n \ll 1でテイラー展開} \int D_z \{ 1 + nN \log (2 \cosh \sqrt{\tilde{q}} z)\} \notag \\ &= 1 + n N \int D_z \log (2 \cosh \sqrt{\tilde{q}} z) \notag \\ &\simeq \exp \left( nN \int D_z \log (2 \cosh \sqrt{\tilde{q}} z) \right) \tag{2.22} \end{align}\]最後の変形は\(n \ll 1\)より再びexponentialに戻すことで得られます。このような操作をすることで\(\int D_z\)を指数関数の肩に移動し、\(\log\)に直接かかるようになります。まとめると
\[\begin{align} S(Q) &= \frac{1}{N} \log \left[ \int d\tilde{Q} \int d\tilde{q} \exp \left\{ -\frac{N}{2} (\tilde{Q}n + q \tilde{q} n (n-1))\right\} \exp \left( \frac{1}{2} nN \tilde{Q} - \frac{1}{2} nN \tilde{q} + nN \int dD_z \log(2 \cosh \sqrt{\tilde{q}} z) \right) \right] \notag \\ &= \frac{1}{N} \log \left[ \int d\tilde{Q} \int d\tilde{q} \exp \left\{ \frac{N}{2} q \tilde{q} n \right\} \exp \left( - \frac{1}{2} nN \tilde{q} + nN \int dD_z \log(2 \cosh \sqrt{\tilde{q}} z) \right) \right] \tag{2.23} \end{align}\]今、\(n \ll 1\)を考えているので、\(n (n-1) \simeq -n\)としました。\(e\)の肩の部分を\(Ng( \tilde{q})\)とおきましょう。すると
\[g (\tilde{q}) = \frac{n}{2} \tilde{q} (q-1) + \frac{n}{2} \int D_z \log(2 \cosh \sqrt{\tilde{q}} z) \tag{2.24}\]これより
\[\frac{\partial g}{\partial \tilde{q}} = \frac{n}{2} (q-1) + \frac{n}{2} \int D_z \tanh (\sqrt{\tilde{q}}z) \frac{z}{\sqrt{\tilde{q}}}\]ここでHubbard-Stratonovich 変換の公式
\[\int D_z z f(z) = \int D_z f' (z) \tag{2.25}\]を用いると
\[\frac{\partial g}{\partial \tilde{q}} = \frac{n}{2} (q-1) + \frac{n}{2} \int D_z (1-\tanh^2 (\sqrt{\tilde{q}}z)) \underbrace{=}_{鞍点法} 0 \ \Longrightarrow \ \therefore \ q = \int D_z \tanh^2 (\sqrt{\tilde{q}}z) \tag{2.26}\]よって
\[[Z^n] = \int dq \ \exp \left[ N \left\{ \frac{\beta^2 J^2}{4} (n \cdot 1 + n (n-1) \cdot q^2) + \left( -\frac{n}{2} \tilde{q} (1-q) + n \int D_z \log (2 \cosh \sqrt{\tilde{q}}z) \right) \right\} \right] \tag{2.27}\]\(N \rightarrow \infty\)より、鞍点法を用いることができます。\(e\)の肩の\(\{ \cdots \}\)部分を\(q\)で微分したものが0という条件より
\[\frac{\beta^2 J^2}{4} \underbrace{n(n-1)}_{\simeq -n} 2 q - \frac{n}{2} \tilde{q} (-1) = 0 \ \Longrightarrow \ \therefore \ \tilde{q} = \beta^2 J^2 q \tag{2.28}\](2.26), (2.28)を合わせて
\[q = \int D_z \tanh^2 (\beta J \sqrt{q} z) \tag{2.29}\]となります。これは強磁性イジングモデルにおける磁化の式\(m = \tanh(\beta Jm)\)と似ている式になっています。しかし\(q \propto \sum x_i^a x_i^b\)より、\(x\)の2次式なので\(\tanh\)が2回出てきています。さらにこの場合は\(m\)に対応する値が\(\sqrt{q} z\)になっています。強磁性イジングモデルのときは\(J_{ij}\)が一様でしたが、今回は\(J_{ij}\)がガウス分布にしたがってランダムになっています。\(z\)はそのゆらぎを表し、スピングラス秩序パラメータはそれによって発生していることが見て取れます。
極低温での\(q\)の振る舞い
(2.29)式より低温極限(\(\beta \rightarrow \infty\))では、\(\tanh (\cdots) = 1\)より\(q \rightarrow 1\)となることがわかります。ここではその値だけでなく、その振る舞いも見てみましょう。\(\tanh^2 = 1- \frac{1}{\cosh^2}\)より
\[q = 1 - \int D_z \frac{1}{\cosh^2 (\beta J \sqrt{q} z)} = 1 - \frac{1}{\beta J \sqrt{q}} \int D_z \frac{d}{dz} \tanh (\beta J \sqrt{q} z)\]\(\beta \rightarrow \infty\)においては、\(f(z) = \tanh (\beta J \sqrt{q} z)\)は下図のような関数の形になります。
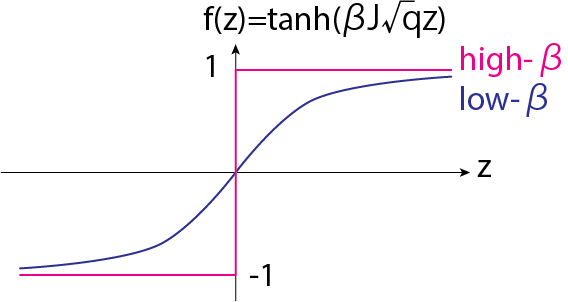
よってこれはヘヴィサイドの階段関数を用いて変形することができて
\[\begin{align} q &= 1 - \frac{1}{\beta J \sqrt{q}} \int D_z \frac{d}{dz} (2 \Theta(z) -1) \underbrace{=}_{\delta(z) = \frac{d\Theta}{dz}} 1 - \frac{1}{\beta J \sqrt{q}} \int \frac{dz}{\sqrt{2\pi}} e^{-\frac{1}{2} z^2} 2 \delta (z) \notag \\ &\underbrace{=}_{q \sim 1} 1 - \frac{1}{\beta J} \sqrt{\frac{2}{\pi}} \tag{2.30} \end{align}\]この式の形から、\(\frac{1}{\beta J} = 0\)から温度を上げていくと、線形で\(q\)が小さくなることがわかります。
Negative entropy
同様に、極低温でのエントロピーの振る舞いを計算してみましょう。
\[S = \frac{\partial F}{\partial T} = \beta^2 \frac{\partial }{\partial \beta} \left[ -\frac{1}{\beta} \log Z\right] \tag{2.31}\]これまでの計算で(2.27), (2.28)式より
\[\begin{aligned} [Z^n] &= \exp \left[ N n \left\{ \frac{\beta^2 J^2}{4} (1 + (n-1) q^2) - \frac{1}{2} \beta^2 J^2 q (q-1) + \int D_z \log(2 \cosh (\beta J \sqrt{q} z)) \right\} \right] \\ &\xrightarrow{n \rightarrow 0} 1 + nN \left\{ \frac{\beta^2 J^2}{4} (1 - q^2) - \frac{1}{2} \beta^2 J^2 q (q-1) + \int D_z \log(2 \cosh (\beta J \sqrt{q} z)) \right\} \end{aligned}\]これと(2.7)式より
\[[\log Z] = \lim_{n \rightarrow 0} \frac{[Z^n]-1}{n} = N \left\{ \frac{\beta^2 J^2}{4} (1 - q^2) - \frac{1}{2} \beta^2 J^2 q (q-1) + \int D_z \log(2 \cosh (\beta J \sqrt{q} z)) \right\}\]これを(2.31)式に代入して
\[S = -N \left\{ \frac{J^2}{4} (1-q^2) + \frac{J^2}{2} q (1-q) - \left( \frac{1}{\beta}の項\right)\right\}\]今、考えているのは極低温\(\beta \rightarrow \infty\)なので
\[S = - \frac{N J^2}{4} (1-q) \{ (1+q) - 2q\} = - \frac{N J^2}{4} (1-q)^2\](2.30)式より
\[S = - \frac{N J^2}{4} \frac{1}{\beta^2 J^2} \frac{2}{\pi} = - \frac{N}{2 \pi \beta^2} < 0 \tag{2.32}\]となります。
オンライン動画の結果と異なります。どこかに計算ミスがある?
エントロピーは状態数を数え上げたものなので、負になることはありません。これはSherrington-Kirkpatrick modelの極低温において、レプリカ対称性(\(q^{qb} = q \ (a \neq b)\))が破れていることから来るものです(Full-step replica symmetry breakingという特別なことが起こっています)。研究をしているとたまこのようなことが起こるので注意してください(実はレプリカ対称性が破れないことの方が多く、SKモデルが特別な場合だったりします)。レプリカ対称性が破られていると、相転移点も異なってきます。
Appendix 1: log公式の導出
レプリカ法で用いた(2.7)式を導出方法を示します。
\[Z^n = e^{\log Z^n} = e^{n \log Z} \underbrace{=}_{n \ll 1} 1 + n \log Z \ \Longrightarrow \ \log Z = \lim_{n \rightarrow 0} \frac{Z^n -1}{n}\]Appendix 2: 平均の取り方とquenched系, annealed系
一般に
\[[\log Z ] \neq \log [Z]\]となります。左辺をquenched, 右辺をannealedと呼びます。左辺の\([\log Z]\)は\(n \rightarrow 0\)の結果ですが、右辺\(\log [Z]\)は\(n=1\)の結果を表します。
Quenchedは\(J_{ij}\)を先に用意し、その中でスピンを動かすような系です。それに対してannealedは\(J_{ij}\)とスピンが両方自由に動くような系です。Annealedの平均の取り方は
のように、スピン\(x\)と\(J_{ij}\)が同じ扱いであり、\(x\)と\(J_{ij}\)の変化がお互いに影響しあいます。これがannealed系(柔らかい系)です。Quenched計算とannealed計算が一致する場合は当然ありますが、それは意味の違うものが一致するというあまり面白くない系でしょう。計算の大変さではquenched系の方が大変、annealed系は簡単とされています。
実際の物質例としては、先に冷やして固めた合金はquenched, 不純物などが動きつつ固まるような物質はannealedです。ニューラルネットワークでは、データを変えずに(固定して)その重みを変えることで最適化を行うとquenched系です。しかし、固定せずに最適化途中でデータを変えるとそれはannealed系です。機械学習の応用ではStochastic gradient method(確率勾配法)と呼ばれる方法があり、スピングラスの考え方を機械学習の理論に用いることができます。
Appendix 3: Hubbard-Stratonovich 変換の公式の導出
\[\begin{aligned} \int D_z z f(z) &= \int \frac{dz}{\sqrt{2\pi}} e^{-\frac{1}{2}z^2} z f(z) = - \int \frac{dz}{\sqrt{2\pi}} \left( \frac{d}{dz} e^{-\frac{1}{2} z^2} \right) f(z) \\ &= - \underbrace{\left[ e^{-\frac{1}{2} z^2} f(z) \right]_{-\infty}^\infty}_{=0} + \int \frac{dz}{\sqrt{2\pi}} e^{-\frac{1}{2} z^2} f'(z) = \int D_z f'(z) \end{aligned}\]参考文献及びリンク
- [1] 大関真之 YouTube動画 “Statistical physics and information processing vol. 1 (情報統計物理) 【Tokyo Tech Lecture Live Streaming】”
- [2] 大関真之 YouTube動画 “Statistical physics and information processing vol. 2A (情報統計物理) 【Tokyo Tech Lecture Live Streaming】”
- [3] 大関真之 YouTube動画 “Statistical physics and information processing vol. 2B (情報統計物理) 【Tokyo Tech Lecture Live Streaming】”
- [4] 高橋和孝・西森秀稔、相転移・臨界現象とくりこみ群