Table of contents
2.3 Radiative transfer equationのモーメント
このページでは輻射輸送方程式(2.5)式の\(\mu (= \cos \theta)\)に対するモーメントを考えましょう。
\[\mu \frac{dI_\nu (\tau_\nu, \mu)}{d\tau_\nu} = I_\nu -S_\nu\]これに何もかけないで立体角の積分を実行します。Flux \(F_\nu\)が
\[F_\nu = \int_{4\pi} \mu I_\nu d\Omega = \int_{4\pi} I_\nu \cos \theta d\Omega\]そして Mean intensity \(J_\nu\)が
\[J_\nu = \int_{4\pi} \frac{J_\nu}{4\pi} d\Omega\]と書けるので
\[\frac{d F_\nu}{d\tau_\nu} = 4\pi (J_\nu -S_\nu) \tag{2.26}\]ただし、\(S_\nu\)は方向依存性がないとしました。このMean intensityは放射のエネルギー密度と関係した量です。ある場所をある方向に進む光を考えるましょう。光は毎秒\(c\)だけ進ので、その光が持つエネルギー密度は\(I_\nu /c\)です。そのような光があらゆる方向から通過するので、その場所での振動数\(\nu\)の放射のエネルギー密度\(U_\nu\)は
\[U_\nu = \frac{1}{c} \int_{4\pi} I_\nu (\theta) d\Omega = \frac{4\pi}{c} J_\nu \ (=\frac{4\pi}{c} B_\nu \ {\rm in \ LTE}) \tag{2.27}\]となります。したがってLTEを仮定すると、全ての振動数の放射のエネルギー密度は
\[U = \frac{4\pi}{c} \int_0^\infty B_\nu d\nu = a T^4 \tag{2.28}\]となります。ここで\(a \equiv 8\pi^5 k_B^4 / (15 c^3 h^3)\)はRadiation constantです。
次に(2.5)式に\(\mu\)をかけて全立体角に対して積分を行います。
\[4\pi \frac{d K_\nu}{d \tau_\nu} = F_\nu \tag{2.29}\]となります。ここで
\[K_\nu \equiv \frac{1}{4\pi} \int_{4\pi} \mu^2 I_\nu (\theta) = \frac{1}{4\pi} \int_0^{2\pi} d\varphi \int_0^{\pi} d\theta I_\nu \cos^2 \theta \sin \theta = \frac{1}{2} \int_{-1}^1 \mu^2 I_\nu (\mu) d\mu \tag{2.30}\]のように定義されます。Source function \(S_\nu (= B_\nu \ {\rm in \ LTE})\)は等方的としているので、\(\mu\)をかけて全立体角で積分すると0になります。
Radiation pressure (輻射圧)
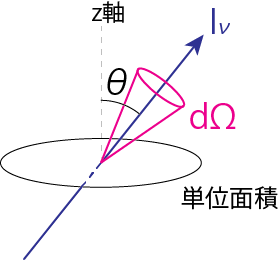
\(K_\nu\)は以下のように輻射圧(Radiation pressure) \(P_{\rm rad}\)と関係づけられます。圧力はある単位面積を単位時間に通過する、その面に垂直な方向の運動量フラックスと定義されます。上図のように、\(z\)方向に垂直な単位面積を考えましょう。天頂角\(\theta\)の方向の微小立体角\(d\Omega\)の方向に進む光が、その面積を毎秒通過するエネルギーは
\[E_\nu (\theta ) d\Omega = I_\nu (\theta ) \cos \theta d\Omega \tag{2.31}\]と書くことができます。光の運動量はエネルギーを光速度\(c\)で割ったものなので、通過する\(z\)方向の運動量は\(E_\nu (\theta ) \cos \theta d\Omega /c\)と書けます。振動数\(\nu\)の光によりRadiation pressure \(P_{\rm{rad}, \nu}\)は、これを全立体角で積分したものとなります。(2.31)式より
\[P_{\rm{rad}, \nu} = \frac{1}{c} \int_{4\pi} I_\nu (\theta) \cos^2 \theta d\Omega = \frac{2\pi}{c} \int_{-1}^1 \mu^2 I_\nu (\mu) d\mu = \frac{4\pi}{c} K_\nu \tag{2.32}\]のように表されます。\(P_{\rm{rad}, \nu}\)を振動数について積分するとRadiation pressure \(P_{\rm{rad}}\)が得られます。
大気の十分深い層では\(I_\nu (\theta )\)の方向依存性が強くないため
\[K_\nu = \frac{1}{4\pi} \int_{4\pi} \mu^2 I_\nu d\Omega \simeq \frac{J_\nu}{4\pi} \int_{4\pi} \mu^2 d\Omega = \frac{J_\nu}{3} \simeq \frac{B_\nu}{3} \tag{2.33}\]となるので
\[P_{\rm{rad}} = \frac{4\pi}{c} \int_0^\infty K_\nu d\nu \simeq \frac{4\pi}{3c} \int_0^\infty B_\nu (T) d\nu = \frac{1}{3} aT^4 = \frac{1}{3} U \tag{2.34}\]となります。(2.29)式を変形して振動数に対して積分することで、Radiation pressureを使って書き換えることができます。
\[(2.29), (2.32) \ \Longrightarrow \ c \frac{d P_{\rm{rad}, \nu}}{d\tau_\nu} = F_\nu\] \[d\tau_\nu = - (\kappa_\nu + \sigma_\nu) \rho dr\]より
\[\frac{d P_{\rm{rad}, \nu}}{dr} = -\frac{1}{c} (\kappa_\nu + \sigma_\nu) \rho F_\nu \ \Longrightarrow \ \frac{d P_{\rm{rad}}}{dr} = - \frac{1}{c} \int_0^\infty (\kappa_\nu + \sigma_\nu) \rho F_\nu d\nu \tag{2.35}\]のように表されます。この式はRadiation pressureの勾配の力(輻射による力)は、輻射を吸収・散乱することに起因するものであることを表しています(発光は等方的に起こるため力を及ぼしません)。