Table of contents
Sunyaev-Zel’dovich Effect (SZE)
銀河団中の高温プラズマの電子(非相対論的電子)によって、宇宙マイクロ波背景放射(CMB)光子が逆Compton散乱を受けます。これによりCMBのスペクトルが歪む現象のことをSZEと呼びます。以下ではこの現象を理解していきましょう。
CMBスペクトルのピーク周波数
CMBは温度\(T \sim 2.73\)Kの黒体放射であり、その放射強度スペクトル(単位時間・単位面積・単位立体角・単位周波数あたりのエネルギー)は
\[I_\nu = \frac{2h}{c^2} \frac{\nu^3}{e^{h\nu/(k_B T)}-1} \tag{1}\]という黒体放射スペクトルで与えられます。宇宙には、一様等方にCMB光子が満ちていいます。
黒体放射スペクトル(1)式が最大強度となる周波数を算出してみましょう。(1)式で\(x=h\nu/(k_B T)\)と置換すると
よって\(f(x)\)の最大となる部分を求めれば、最大強度となる周波数が分かります。それには微分したものが0であれば良いので
\[\frac{df}{dx} = \frac{3x^2 (e^x-1)-x^3 e^x}{e^x-1} = x^2 \frac{3(e^x-1)-xe^x}{e^x-1} = 0 \ \Longrightarrow \ (x-3) e^{x} + 3 = 0\]これを解けば良いことが分かります。
\[(x-3) e^{x-3} = -3 e^{-3}\]のように変形すると、この解はLambert W関数で表されるので
\[x - 3 = W(-3 e^{-3}) \ \Longrightarrow \ x \sim 2.82\]と求まります。
Newton法などの数値計算から求めることも可能です。
以上より
\[h \nu \simeq 2.82 k_B T \tag{2}\]これをWienの変位則と呼びます。実際にCMB光子の温度を代入して周波数を計算しましょう。
\[\nu \sim \frac{2.82 c}{2 \pi \hbar c} \frac{2.73 \mathrm{K}}{10^4 \mathrm{K}} \mathrm{eV} \sim \frac{1.4 \times 10^{10} \mathrm{cm/s}}{200 \mathrm{MeV} \cdot \mathrm{fm}} 2.7 \times 10^{-4} \mathrm{eV} \sim 0.7 \times 2.7 \times 10^{11} [\mathrm{s}^{-1}] \sim 190 [\mathrm{GHz}]\]より厳密に計算を行うと、160GHz程度となります。
Rayleigh-Jeansの法則
Rayleigh-Jeans極限\((h\nu \ll k_B T)\)のとき、(1)式は
\[I_\nu \simeq \frac{2h}{c^2} \frac{\nu^3}{\left(1+\frac{h\nu}{k_B T} \right) -1} = \frac{2k_B T\nu^2}{c^2} \tag{3}\]となります。長波長側は古典的な極限と考えられるため、量子力学的な効果を表すプランク定数\(h\)が消えた形となります。
SZEとCompton y parameter
以下ではRayleigh-Jeans極限で現象を考えましょう。CMB光子が温度\(k_B T = 10\mathrm{keV}\)、電子数密度\(n_e = 10^{-3} \mathrm{cm}^{-3}\)、半径\(L = 1 \mathrm{Mpc}\)の球形の銀河団プラズマ領域を通過したとしましょう。CMB光子がこの領域の電子によって逆Compton散乱を受けると放射強度\(I_\nu\)はどうなるでしょうか。そのためには以下のように、\(\nu \sim \nu + \Delta \nu\)の振動数にある光子の数の変化を考えます。
\(\Delta \nu, \Delta \nu' \ll 1\)とします。\(\nu \sim \nu + \Delta \nu\)にいる光子数は\(\frac{I_\nu}{h\nu} \Delta \nu\)です。同様に\(\nu' < \nu\)において\(\nu' \sim \nu' + \Delta \nu'\)にいる光子数も\(\frac{I_{\nu'}}{h\nu'} \Delta \nu'\)と書けます。\(\nu' \sim \nu' + \Delta \nu'\)の光子のうちの何割かが逆Compton散乱によってエネルギーを獲得し、\(\nu \sim \nu + \Delta \nu\)の仲間入りします。しかし、\(\nu \sim \nu + \Delta \nu\)に元々いた光子の何割かも逆Compton散乱によってエネルギーを獲得し、\(\nu \sim \nu + \Delta \nu\)の振動数から出ていってしまいます。
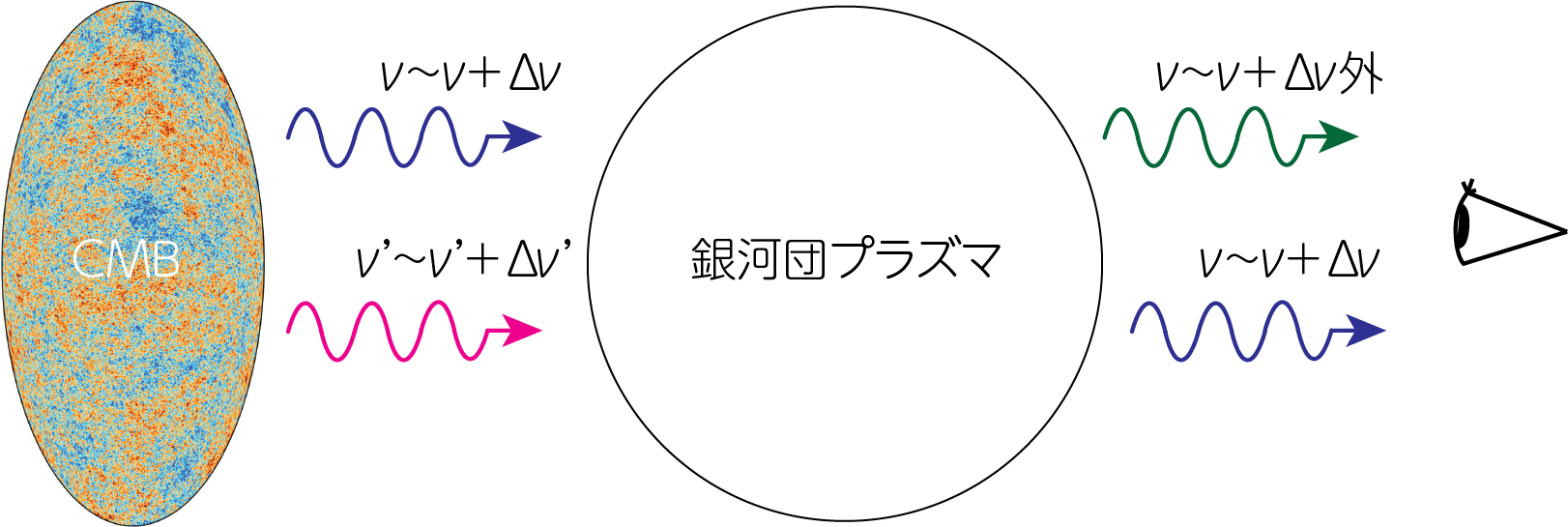
逆Compton散乱を受ける確率は光学的厚み
\[\tau = \frac{L}{\mathrm{mean free path}} = \sigma_\mathrm{T} n_e L \simeq 2 \times 10^{-3} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right) \left( \frac{L}{1 \mathrm{Mpc}}\right)\]によって決定されます。この量は光子のエネルギー(電磁波の振動数)に依存しません。よってこのプラズマ領域を通過した後の強度変化を\(\Delta I_\nu\)とおくと、先ほどの\(\nu \sim \nu + \Delta \nu\)にいる光子数変化の議論より
\[\frac{\Delta I_\nu}{h\nu} \Delta \nu = \left( \frac{I_{\nu'}}{h\nu'} \Delta \nu' - \frac{I_{\nu}}{h\nu} \Delta \nu \right) \tau \ \Longrightarrow \ \Delta I_\nu = \left( \frac{\Delta \nu'}{\Delta \nu} \frac{\nu}{\nu'} \frac{I_{\nu'}}{I_\nu} -1 \right) I_\nu \tau \underbrace{=}_{(3)} \left( \frac{\Delta \nu'}{\Delta \nu} \frac{\nu'}{\nu} -1 \right) I_\nu \tau\]\(h \nu'\)から\(h\nu\)になった光子のエネルギー変化の関係式は逆Compton放射強度で求めた光子のエネルギー増加率より
\[h \nu' \left( 1 + \langle \frac{\Delta \epsilon}{\epsilon} \rangle \right) = h\nu \ \Longrightarrow \ \frac{\nu'}{\nu} = \frac{1}{1+ \langle \frac{\Delta \epsilon}{\epsilon} \rangle } \simeq 1- \langle \frac{\Delta \epsilon}{\epsilon} \rangle \tag{4}\]です。途中\(\langle \frac{\Delta \epsilon}{\epsilon} \rangle \ll 1\)として近似を行いました。同様に\(h(\nu' + \Delta \nu')\)から\(h(\nu + \Delta \nu)\)になった光子のエネルギー変化の関係式は
\[h (\nu' + \Delta \nu')\left( 1+ \langle \frac{\Delta \epsilon}{\epsilon}\rangle \right) = h (\nu+ \Delta \nu) \ \Longrightarrow \ \left( 1+ \langle \frac{\Delta \epsilon}{\epsilon}\rangle \right) \nu' + \left( 1+ \left< \frac{\Delta \epsilon}{\epsilon}\right>\right) \Delta \nu' = \nu + \Delta \nu\](4)式の途中式から
\[\left( 1+ \langle \frac{\Delta \epsilon}{\epsilon} \rangle \right) \Delta \nu' = \Delta \nu \ \Longrightarrow \ \frac{\Delta \nu'}{\Delta \nu} = \frac{1}{1+ \langle \frac{\Delta \epsilon}{\epsilon} \rangle} \simeq 1- \langle \frac{\Delta \epsilon}{\epsilon} \rangle\]以上より
\[\Delta I_\nu \simeq \left\{ \left( 1- \langle \frac{\Delta \epsilon}{\epsilon}\rangle \right)^2 -1 \right\} I_\nu \tau \simeq -2 \langle \frac{\Delta \epsilon}{\epsilon} \rangle I_\nu \tau = -2 y I_\nu \tag{5}\]ここで
\[y \equiv \langle \frac{\Delta \epsilon}{\epsilon} \rangle \tau \simeq 8 \times 10^{-5} \left( \frac{k_B T}{5 \mathrm{keV}} \right) \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}} \right) \left( \frac{L}{1 \mathrm{Mpc}} \right) \tag{6}\]はCompton y parameterと呼ばれ、逆Compton散乱による光子系全体の平均のエネルギー変化率を表します。\(\tau\)は光子が電子により散乱を受ける平均回数であることから、(6)式は\(\tau \ll 1\)のときの定義です(もし\(\tau \gg 1\)ならば、領域通過に伴い何度も散乱を受けるため、複数回のエネルギー獲得を考慮する必要があります)。
上述の議論では銀河団プラズマの典型的な値を代入してきました。これは銀河団プラズマによってCMBスペクトルが歪む現象が起こるからです。この現象を、初めて指摘した理論家の名前をつけてSunyaev-Zel’dovich Effect(SZE)と呼びます。
CMB放射強度\(I_\nu\)のグラフ全体が以下のように高周波数側に平行移動するため、低周波側では強度が減少(decrement)し、高周波側では強度が増加(increment)します。このとき、典型的には217GHzでは\(\Delta I_\nu = 0\)となることが知られています。
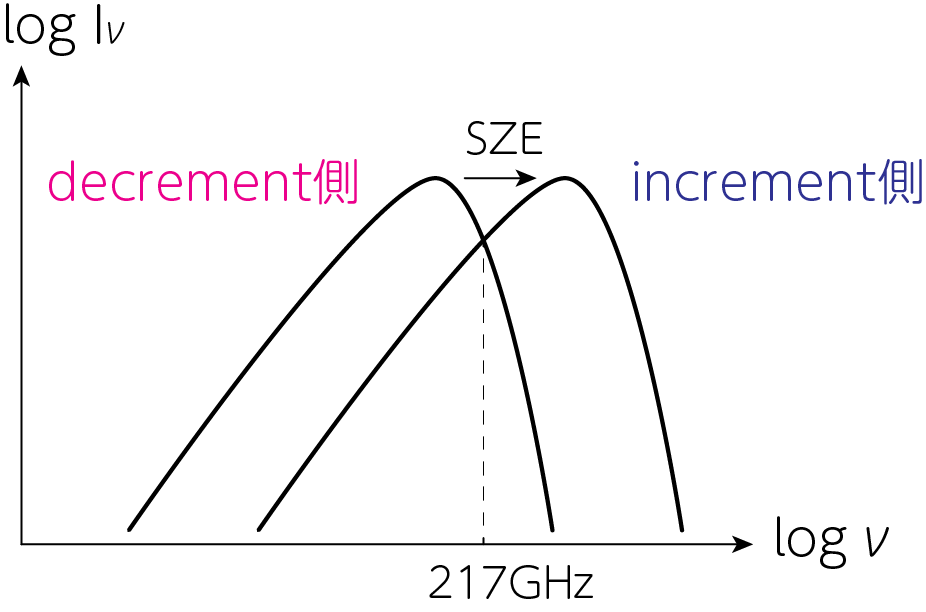
下図は実際に銀河団観測から示されたSZEです。低周波数では暗く(青色)、高周波数では明るく(赤色)なっている様子がわかります。217GHzでは変化がない(緑色)こともわかります。

多くのSZEの研究論文ではCompton y parameterの定義として、逆Compton放射強度の光子のエネルギー増加率の\(k_B T\)の係数4を省いたものを用いているため、注意が必要です。
参考文献
- [1] Lambert W-function
- [2] Planck CMB map
- [3] Multi-band obesrevations of the galaxy cluster ABELL 2319